一種提高相位測距精度的方法

曾 真，王元慶

(南京大學電子科學與工程學院，江蘇南京210093)

1 引言

現有測相方法主要可以分為自動數字測相法、數字同步解調法、頻域數字測相法。而頻域數字測相方法與其他測相方法相比有以下的優點:首先，頻域數字測相方法的測距精度很高，同等條件下頻域數字測相的測相誤差為數字同步解調方法的二分之一;且由DSP對數字序列做N點FFT變換，速度快，電路實現簡單［1］;其次，由于設計為相位敏感系統，當信號的幅度有所變化時，若使用DSP做信號處理，測相器有固定的相位分辨率，可以克服由于模擬信號的幅度變化引起的測相誤差;再次，頻域數字測相方法的測相速度快，計算量比較小，特別是在位數較多的時候，這一優點更加明顯，在實際應用中更能體現出實時的特性［2］。現普遍使用的頻域數字測相方法為FFT譜分析法［2－3］，由于FFT和譜分析只能在有限區間內進行，這就不可避免地存在由于時域截斷產生的能量泄漏，而譜線的離散化也不可避免地產生柵欄效應，使譜峰值變小，相位精度降低。為了提高相位測距的精度，本文選用了密集頻譜細化及校正的方法，并使用了傳統方法與本文方法對仿真的激光回波信號進行對比研究。

2 相位式激光雷達測距原理

激光相位測距的基本原理是通過發射強度調制的激光照射目標，使用高敏感度的光電器件，如APD，采集反射回來的信號。通過計算發射信號與回波信號之間的相位差Δφ，即可以得到目標的距離值 d，計算公式如下［4］:

其中，c為光速;f0為激光的調制頻率;N為發射信號與回波信號相差的整數個波數。從式(1)可以看出，發射信號與回波信號之間的相位差Δφ的精度決定了測距的精度［5］。

加Hanning窗時，只進行單諧波頻率成分的幅值恢復時的最大誤差仍高達15．3%，相位誤差更高達90°。而對于一個頻率為20 kHz的理想正弦信號，使用200 kHz的采樣頻率采256個點，此時頻率分辨率為頻率分辨率即 781．25 Hz，頻率結果誤差高達4%，相位的測量精度不高［7］。其中，相位的測量精度又是由譜線查找和相位計算精度決定，因而本文使用復調制細化選帶頻譜分析方法提高譜線查找精度，相位差校正法提高相位計算精度。

3 相位精確估計方法的選用

3．1 復調制細化選帶頻譜分析算法

復調制細化選帶頻譜分析方法使用復解析帶通濾波器，復調制移頻點數為傳統方法的1/D，較傳統復調制細化選帶頻譜分析方法計算量小。它不但降低了FFT的點數［8］，計算量小，且所需的內存空間也少得多，而且也不需要進行復雜的頻率調整［9－12］。由于激光相位測距中數據量大，實時處理要求高，因而采用一級FIR復解析帶通濾波器，能保證分析的精度誤差在1%以內。具體的作法如下:先確定中心頻率及細化倍數，在頻率(f1－f2)范圍內進行頻率細化分析，則再構造一個寬度為1/D的復解析帶通濾波器，對樣本信號作選抽濾波。選抽后的信號進行復調制移頻，將細化的起始頻率移到零頻點，最后做N點FFT和譜分析，不需要進行頻率調整就可以得到具有N條獨立譜線的細化頻譜。其數據處理的流程如圖1所示。最后得到的細化頻譜譜線間隔為普通FFT的1/D，即在幅度譜上找到相應發射頻率的頻譜精度提高D倍［8］。復調制細化選帶頻譜分析方法可以細化譜線間隔，從而提高譜線查找的精度。

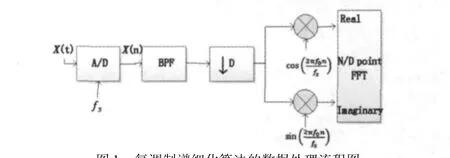
圖1 復調制譜細化算法的數據處理流程圖Fig．1 data processing flow chart ofmultiple modulation zoom spectrum analysis algorithm

3．2 相位差校正法

在常用的四種校正方法中，比值校正法和能量重心校正法是一種近似的校正方法，FFT+FT連續細化傅里葉變換法計算量大，而相位差法得到的是真實解且相位的校正不依賴于窗譜函數，因而采用相位差校正法。

先對原始單頻率成分信號采(L+N)點樣本，然后對這1到N和L到(L+N)兩段信號分別進行作傅里葉變換，利用其對應離散譜線譜峰處的相位差進行校正。第一段的峰值譜線號i(i=0，1，2，…，N－1)，設頻率校正量為Δf=difs/N，其中di為歸一化的譜線號修正量［9］，其值范圍為［－ 0．5，0．5］。第二段進FFT(或DFT)后與之對應的峰值譜線號為i，T=N/fs，有相位差［7］:

設信號FFT的實部為Ri，虛部為Ii，由對稱窗函數相位特點，歸一化頻率校正量為di時，則校正后的相位為:

4 激光相位測距的仿真計算與比較

設定發射信號頻率f0=3 MHz，采樣頻率為fs=32 MHz，f1為信號歸一化頻率。加Hanning窗，進行整型FFT變換，進行選抽濾波之后做N=4096的FFT變換。利用計算機生成仿真的激光發射和回波信號:

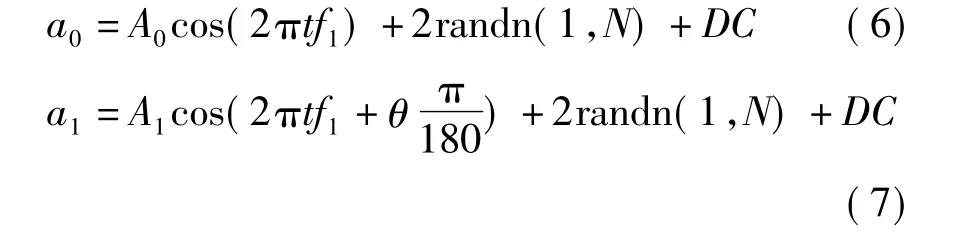
對于激光相位式測距，距離信息是由發射信號與接收信號的相位差計算得到的，因而對于測距有意義的是兩信號間的相位差值。使用密集頻譜細化及相位差校正法和傳統方法得到兩相位差值的分析結果(其中細化倍數為150倍，中心頻率為3 MHz，采用一級FIR濾波器，濾波半階數為500)。本文方法與傳統方法的仿真計算角度值如圖1所示，誤差結果如圖2所示，測距結果如表1表示。

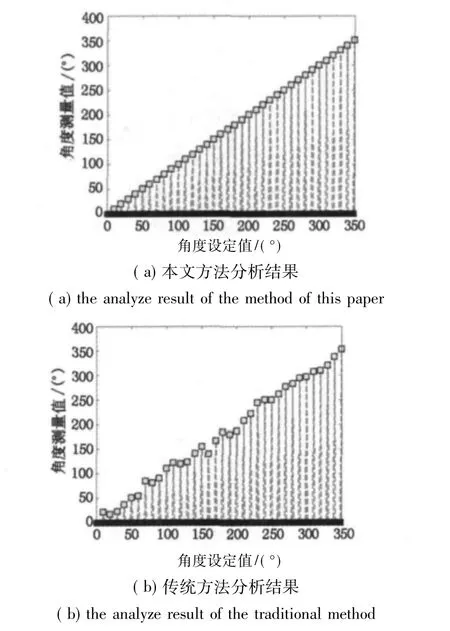
圖2 本文方法與傳統方法分析結果Fig．2 results of the proposed method and the traditional one

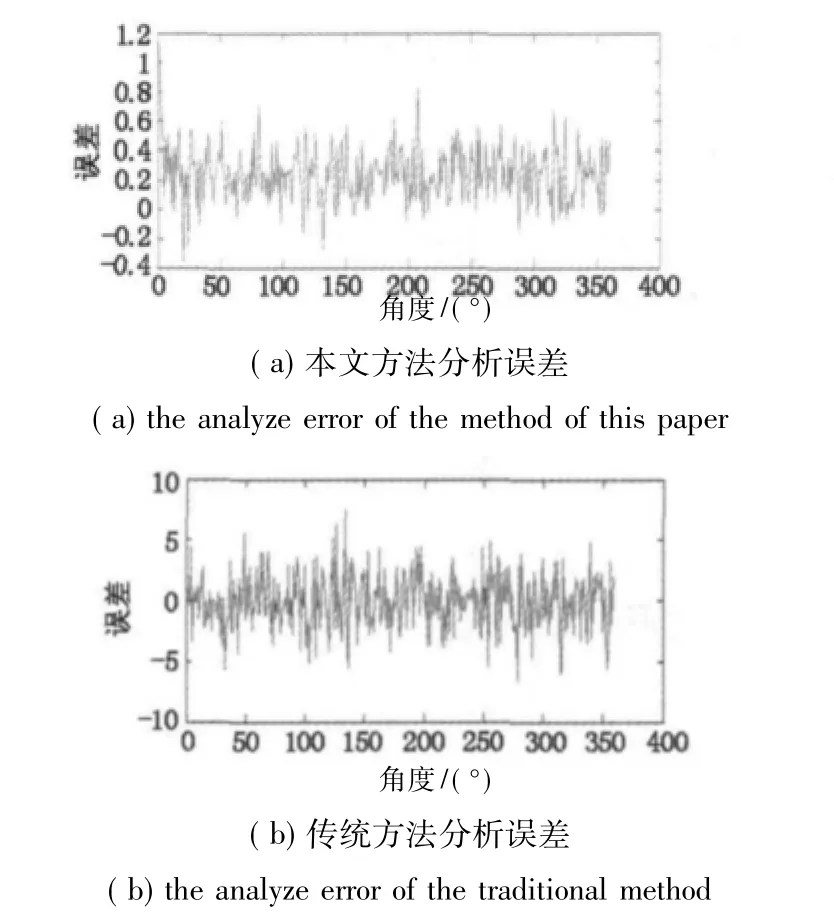
圖3 本文方法與傳統方法分析誤差Fig．3 errors of the proposed method and the traditional one

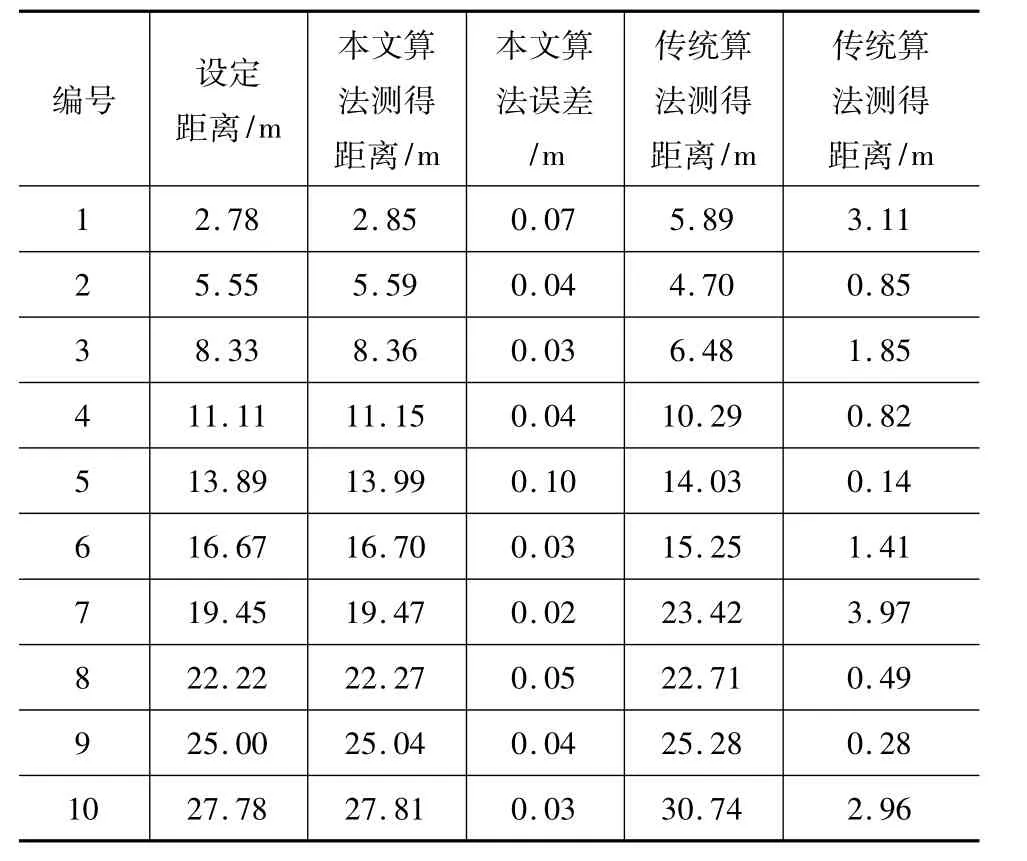
表1 測距結果對比表Tab．1 comparing table of the ranging result

從以上數據可以看出，相位誤差高達10°，即對于3 MHz的發射頻率，測距精度為3 m，只能通過增加FFT的點數來提高精度。本文采用先進行頻譜細化，再進行頻譜校正的方法，誤差最大僅為1°即對于3 MHz的發射頻率，測距精度為0．3 m。克服了頻域數字測相法分辨率不高的缺陷。

4 結論

在傳統的相位測距方法中，只能通過增加FFT的點數來增加相位計算的精度，使得運算量增加、速度降低。相比較而言，頻譜細化算法中基于復解析帶通濾波器的復調制譜細化算法所需的運算量少，計算速度最快;頻譜校正算法中相位差校正算法校正是一種精確地校正方式，校正精度很高;頻譜細化和頻譜校正技術能大大提高頻譜分辨率。在工程應用中，本文方法運用于激光相位測距中能大幅度提高頻域數字測相的精度。

［1］ Zhang Ting，et al．Study of phase-shift laser measuring based on matlab［J］．Laser ＆ Infrared，2010，40(1):22 －27．(in Chinese)張婷，等．基于Matlab的相位式激光測距研究［J］．激光與紅外，2010，40(1):22 －27．

［2］ Hui Zhang．The realization of laser distance-measuring equipment on embedded system［D］．Shanghai:Tongji U-niversity，2007．(in Chinese)張慧．相位法激光測距算法的嵌入式系統實現［D］．上海:同濟大學，2007．

［3］ Xie Lei，Li Ji．Realization of digital phase detector based on FFT algorithm in laser distance measurement system［J］．Chinese Journal of Quantum Electronics，2003，20(1):85 －88．(in Chinese)謝蕾，李季．基于FFT的激光測距數字相位計的實現［J］．量子電子學報，2003，20(1):85 －88．

［4］ Wang Tao．Research of the phase laser ranging techonology［J］．Laser ＆ Infrared，2007，37(1):29 － 31．(in Chinese)汪濤．相位激光測距技術的研究［J］．激光與紅外，2007，37(1):29 －31．

［5］ Gao Song．The research on some key questions about digital phase laser range measurement system［D］．Dalian:Dalian Maritime University，2007．(in Chinese)高篙．數字鑒相式激光測距系統幾個關鍵問題的研究［D］．大連:大連海事大學，2007．

［6］ Jin Yanhua．Study of a novel zoom spectrum analysis，international conference on communications and mobile computing［J］．Communications and Mobile Computing，2009，(1):367－371．

［7］ Ding Kang，et al．Synthesized correctingmethod of phase difference on discrete spectrum［J］．Journal of Vibration Engineering，2002，15(1):114 －119．(in Chinese)丁康，等．離散頻譜綜合相位差校正法［J］．振動工程學報，2002，15(1):114 －119．

［8］ Jing Gai．Frequency estimation of uncooperative coherent pulse radars ［J］．Military Communications Conference，2007:1－7．

［9］ QiGuoqing．Analysis of the influence of observation starting time on FFT-based phase estimation of sinusoid［J］．Signal Processing(ICSP)，2010:26 －29．

［10］ Jiang Bo，etal．Research and realization ofmultiplemodulation ZoomFFT algorithm in partial Zoom spectrum analysis［J］．，2010，(7):48 －49．(in Chinese)江波，等．基于復調制的ZoomFFT算法在局部頻譜細化中的研究與實現［J］．大眾科技，2010，(7):48 －49．

［11］ Ding Kang，Xie Ming，et al．Principle and method ofmultiplemodulation zoom spectrum analysis based onmultiple analytical band-pass filter［J］．Journal of Vibration Engineering，2001，14(1):30 －35．(in Chinese)丁康，謝明，等．基于復解析帶通濾波器的復調制細化譜分析原理和方法［J］．振動工程學報，2001，14(1):30－35．

［12］ Shang Haitao，Xue Hongxi．Study on the ZoomFFT algorithm based on band-pass filter［J］．Process Automation Instrumentation，2011，32(4):10 －12．(in Chinese)尚海濤，薛紅喜．基于帶通濾波器的ZoomFFT算法研究［J］．自動化儀表，2011，32(4):10 －12．