拉伸彎曲矯直理論及仿真研究綜述

陳 兵，舒建華，郭瑞娟，張 靜

(北京科技大學機械工程學院，北京 100083)

0 前言

拉伸彎曲矯直機的板形矯正工藝原理就是依靠張力輥及彎曲輥的共同作用，使帶材在所承受的張力小于屈服極限的情況下，產生局部塑性延伸，進而實現改善板形的目的。由于其“巧奪天工”的技術，受到廣泛重視，現已成為各大鋼廠冷軋帶鋼生產線的重要設備。對拉矯機的研究有將近半個世紀，本文對拉彎矯直理論及仿真研究進行總結歸納，并對未來發展進行了展望。

1 拉矯理論的研究

1969 年日本學者曾田長一郎認為［1］:對于彈塑性體，在彎曲和彈復的全過程中，中性面都移向壓縮面一側，即中性面相對于中間層的偏移。帶鋼的中間面被拉伸，在反復彎曲過程中，其延伸率可以采用疊加計算的方法。在此基礎上，給出了理想彈塑性材料的帶鋼在反復拉伸彎曲過程中，長度方向的應力和應變沿厚度方向分布狀態的變化，為后來學者對拉伸彎曲變形過程基本認識奠定了基礎。1976 年MISAKA 發表文章首先提出了薄寬帶鋼拉伸彎曲變形分析的五點基本力學簡化［2］:(1)由于帶鋼薄且寬，帶鋼的變形是平面應變變形;(2)忽略厚度方向的應力;(3)變形前的橫斷面變形后仍保持為平面;(4)應力沿寬度方向均勻分布，且忽略矯直過程中的張力變化;(5)忽略材料的包辛格效應。在以上假設基礎上，基于塑性增量理論對帶鋼沿厚度方向上的應力應變沿厚度方向的分布進行了研究。五點基本假設條件和胡克定律成為之后研究帶鋼拉伸彎曲變形理論的通用條件。

1971 至1979 年Sheppard 在先后發表的數篇文章中，提出在拉伸彎曲矯直過程中引起的應變足以在拉伸側和壓縮側產生屈服，描述了帶鋼長度方向應力沿厚度方向的分布，并給出了離中心層距離為Z 的纖維層的縱向應變表達式［3-6］。1972～1982 年E.J.Patula、余同殺［7-8］參考梁彎曲模型，將帶鋼拉伸彎曲變形提出了3 種應力分布形式的假設。1982 年劉啟森［9］引入相對變形率推導了各種相對變形率之間的關系。但是李同慶［11］指出其致命缺陷，認為將拉彎過程考慮成彎曲變形與拉伸的簡單線性迭加是行不通的。1989 年徐守國［10］主要研究浪形的矯正問題，并給出了拉伸彎曲矯直后帶材平直的判別式。1997年至1999 年李同慶、肖林［11-12］等先后對帶鋼拉伸彎曲變形過程進行了研究。肖林對之前的3 種應力分布形式細化為5 種應力分布形式。提出了只有當帶鋼的塑性變形區域超過帶鋼截面的50%，中間層才能產生塑性應變。之后，國內學者崔甫、李忠富、張清東［13-14］等人基本都沿用了肖林的5 種應力分布形式的假設。2010 年崔甫［15］在其新書里提出增加等曲率區這一概念，認為當壓彎量增大到一定的時候，反彎曲率不會增大而處于等曲率區。等曲率區越長為帶材提供的變形時間越充裕，對滯后變形的彌補越充分，矯直質量越好。

以往對拉伸彎曲變形的研究都是基于梁彎曲理論。2008 年王文廣［16］在博士論文中考慮厚度方向上的應力應變，采用板彎曲的求解思路對帶鋼進行理論建模。但其計算出的結果與實際仍有較大差距。

1.1 彎曲曲率

帶鋼在拉伸和彎曲的共同作用下產生彈塑性變形，彎曲的作用不言而喻。在關于拉伸彎曲變形帶鋼應力應變分布的理論建模研究中，彎曲曲率作為反映帶鋼彎曲程度的重要參量，是拉矯解析模型中能否進行計算的關鍵。

早期研究拉矯機理時，認為帶鋼的彎曲半徑與輥的半徑一致。但拉伸彎曲變形過程中，帶鋼并未與彎曲輥面完全貼合，其接觸面的曲率半徑不一定等于彎曲輥輥徑、而是由張力、彎曲輥輥徑，輥距、帶鋼材料屬性等參數共同決定的。1972 年T.sheppard［4］提出帶鋼曲率半徑是否等于彎曲輥半徑的判定條件。但對計算帶鋼的彎曲曲率半徑的研究價值不大。1984 年，NE.Thompson［17］認為兩個彎曲輥之間的自由帶材近似一條直線，但顯然這樣對帶材與彎曲輥接觸點的位置的假設是難以接受的。1994 年，洪麗英等人［18］假定帶鋼受力后，成為一條拋物線形狀并假設這條拋物線是表示帶鋼曲率變化的主要函數。但其中假設過多，存在明顯缺陷。1997 年，肖林［12］結合NE.Thompson 的工作，對理想彈塑性和線性強化帶材在彎曲輥上的最小曲率半徑的計算方法進行了探討。并給出了帶鋼與輥線接觸時的最小彎曲曲率計算模型。但涉及到的計算公式需要進一步的改進和修正。Yoshisuke［6］在實驗的基礎上總結了一套有效的經驗公式

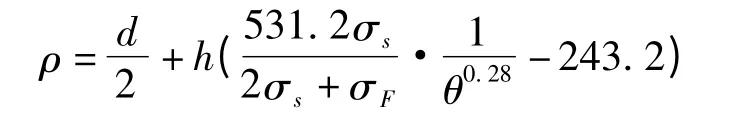
式中，ρ為帶鋼彎曲半徑，d為彎曲輥直徑;h為帶鋼厚度;s為帶鋼屈服極限;σF為帶鋼橫截面張應力;θ為帶鋼包角。

后來，李忠富、鄧凱［19］等人在經驗半徑公式的基礎上，根據大量現場離線數據修正了半徑公式。但修正的公式不能通用。

1.2 張力變化計算

帶鋼張力也是拉伸彎曲矯直的一個重要參量。最開始人們忽略拉矯機的張力變化，到上世紀90 年代末，李同慶、肖林等都認識到，在理論建模中假設帶鋼張力在拉伸彎曲矯直過程中保持不變并不正確，實際生產中帶鋼張力是不斷變化的。并且帶鋼發生拉伸彎曲變形所需的變形能必須要有張力做功提供。從后張力輥組到前張力輥組，帶鋼的張力是逐漸增大的，帶材的張力變化與帶材的彎曲能耗有關系。單位寬度單位長度帶鋼內部功可用拉伸功和彎曲功的和來表示。而計算變形功需要知道帶材橫截面上的應力和應變情況的詳細的描述。但彎曲之后帶鋼的應力應變是可知的，而在離開彎曲輥后殘余應力和應變的分布卻難以預知。

1997 年李同慶［11］在其博士論文中認為帶材在拉伸彎曲矯直中，張力的變化主要用于使帶材產生塑性變形。因此，根據拉彎后的塑性應變與對應的應力的乘積，在橫斷面上的積分，就為單位長度，單位寬度上消耗的功。后面也有學者認為塑性應變應為彎曲卸載后由變形協調關系而產生的斷面塑性應變。兩者存在略微差別。1999年肖林［12］根據功能互等原理，建立彎曲輥前后帶鋼張力增量計算模型。但認為彎曲輥前后帶鋼運行速度相等的假設是不符合實際情況的，其所造成的誤差仍是值得討論的問題。而且，采用基于張力不變假設條件的拉伸彎曲變形理論計算帶鋼張力變化本身就是矛盾所在。劉琨明［20］等在很大假設情況下計算了理想彈塑性材料在拉伸彎曲矯直時能耗和張力的變化。并且認為當帶材的彎曲曲率很大時或厚度很大時，帶材的橫截面明顯不是平面，相應的拉伸彎曲能耗的計算公式則會不同。

1.3 延伸率的計算公式

帶鋼浪形的實質是纖維的長短不一。帶材在軋制過程中由于各條縱向纖維不均勻延伸使內部產生壓應力，當其值達到一定程度時，會造成板形的瓢曲或浪形。拉伸彎曲矯直機改善板形正是通過使各條縱向纖維長度相等而實現的。需矯平的帶材在張力輥組施加的張力作用下，連續經過上下交替布置的小直徑彎曲輥劇烈彎曲，帶材各條縱向纖維在拉伸和彎曲應力的聯合作用下，沿長度方向產生了不同程度的塑性延伸，各條縱向纖維的長度趨向于一致，從而減小內應力的不均勻分布，由縱向纖維長度差造成的板形缺陷得以消除［11］。而中間層塑性應變是衡量帶鋼延伸率的標準。

在推導延伸率計算公式時，一般認為帶鋼經過第一個彎曲輥時是沒有原始曲率的。中間層的塑性變形為應變量減去彈性變形量。為保持變形前的橫斷面變形后仍保持為平面這一假設，該彈性變形量為張力引起的彈性變形量，而不是極限彈性量。

1997 年李同慶［11］認為帶材的實際延伸率的大小與每次彎曲的彎曲半徑及張力密切相關，中心層剩余延伸率為

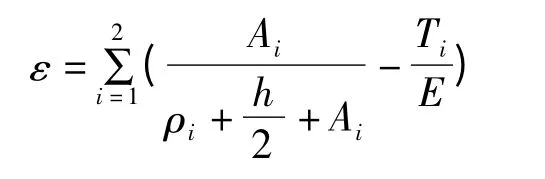
式中，Ai為第i 次彎曲時中性層的偏移量;ρi為第i 次彎曲時帶鋼彎曲曲率半徑;Ti為第i 次彎曲時的前張力;h為帶材厚度。

1999 年肖林［12］認為經過在第一個彎曲輥上的拉伸彎曲之后，帶材存在較大的殘余變形。所以，當分析帶材在第二個彎曲輥上的拉伸彎曲時，必須考慮此殘余曲率。中間層的應變為

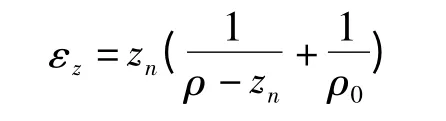
式中，ρ為帶材中間層的彎曲半徑;ρ0為原始彎曲半徑;zn為中性層偏移量。

2004 年，崔甫［13］認為在有殘余曲率的情況下，帶材在彎曲時的總彎曲曲率為

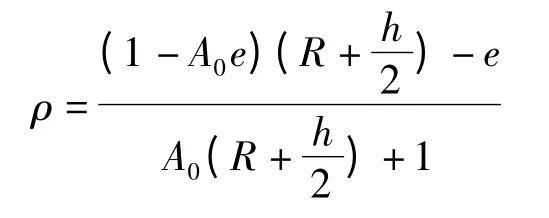
式中，A0為殘余彎曲曲率，R為彎曲輥的半徑，e為中性層偏移量。

2008 年，汪建春［21］推導了帶材中間層應變計算公式

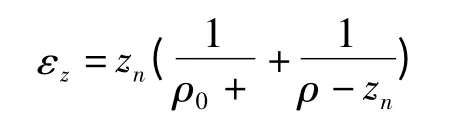
顯然，李同慶意識到張力損耗對延伸率計算的影響;崔甫認為:當帶材的殘余曲率為0 時，帶材的最小彎曲半徑為彎曲輥的半徑，這與之前的分析相悖，因此這種計算方法值得商榷。而且在其著作中也沒有明確描述中間層的延伸率計算公式;汪建春認為拉彎與純彎的應變的曲率關系形式相同，但反彎曲率為中性層反彎曲率。雖然推導方法與肖林不同，但結果與肖林的計算結果一致。這里也可以明顯看出，彎曲半徑經驗公式沒能夠考慮殘余曲率的影響。

2 彎曲與張力配置關系

在拉矯工藝中，延伸率、矯直張力和彎曲曲率是三個重要的參數:延伸率可根據來料確定，而后兩者通常按如下原則確定:1)張力最小原則，盡量利用彎曲對帶材延伸率的貢獻來選工藝參數。較小張力不但可以降低對機組電動機的功率要求，還能減少斷帶和打滑。2)根據拉矯機能夠產生的最大彎曲曲率選擇較小的矯直張力。而張力與彎曲作用的不合理配置，容易引起帶材延伸率不足或過大、能耗過大、功率分配不均、張力波動、帶材矯直后翹曲等問題［22］。

1999 年肖林采用5 種應力分布形式假設，認為只有當應力分布形式為C、E 型時，帶材中間層才能加大塑性延伸。通過應力分布條件圖，可以在一定程度上為彎曲曲率和張力的配置提供依據。2006 年，重慶大學傅玉勇［23］在帶材極限彎曲曲率的計算方法的基礎上，引入極限彎曲曲率修正系數，探討其取值規律，并將極限彎曲曲率修正值作為拉矯時的最大曲率，得出拉矯時最大彎曲曲率和最小張力的確定方法。2007 年燕山大學劉妍［24］編制相應程序，定量分析了張力和彎曲曲率匹配關系變化對拉伸彎曲矯直后帶材內部殘余應力的影響。具有一定的指導意義。

3 板形的矯正

1978 年Yoshisuke MISAKA［6］等學者針對帶鋼拉伸彎曲矯直過程中出現C 翹、L 翹的問題，提出通過外力卸載后帶鋼殘余應力形成的縱向彎曲判斷是否產生了L 翹，通過帶鋼殘余應力形成的橫向彎曲判斷是否產生了C 翹。1989 年徐守國等研究了帶材缺陷的拉伸彎曲矯直的問題［10］，認為拉矯延伸率沿寬度方向分布與初始延伸率偏差分布剛好正負相反、大小相等。給出了在具有對稱邊浪的帶材在彈塑性拉彎狀態下，產生的新延伸率的分布規律。1997 年李同慶［11］總結了帶鋼板形缺陷經拉伸彎曲矯直后產生的新延伸率分布。其結論‘初始延伸率偏差越大的區域在拉伸彎曲矯直后產生的塑性延伸率越小，帶鋼張力越大所產生延伸率越大’等規律符合生產實踐和經驗認識。但關于拉矯延伸率在寬度方向分布剛好與帶鋼初始延伸率偏差的橫向分布正負相反大小相等的假設過于理想。2003 年鄧凱［19］根據板形理論求解出具有初始平坦度缺陷帶鋼的張應力橫向分布，假設帶鋼曲率半徑在寬度方向上均布，基于拉伸彎曲變形理論求解模型建立延伸率橫向分布計算模型。在一定程度上解釋了板形平坦度缺陷矯正原理。2007 年劉妍［24］將前人的基本理論公式應用于帶材的拉伸彎曲矯直定量分析。利用應變函數和應力函數的關系和條元分割的方法，考慮初始殘余應力沿板寬橫向分布值，分析了拉伸彎曲矯直后殘余應力與屈曲變形的關系。

4 數值法仿真

很多文獻通過力求一個簡單的解析式或者編程的手段來描述拉矯過程［19-24］。但由于拉彎矯直過程涉及拉彎、彈復、反彎、硬化等多方面問題，變形十分復雜。很多因素是在解析法中沒有考慮的，所計算出的理論結果跟實際也就相差很遠。

自2000 年以來，隨著有限元軟件的日趨成熟和計算機性能的極大提高，在國外公開發表的文獻基本都是基于有限元方法或者有限元與實驗相結合的研究工作。利用有限元對帶鋼拉伸彎曲變形過程進行仿真研究，張力變化、彎曲曲率、延伸率及帶鋼與彎曲輥間接觸力都可以直接提取，而關鍵在于模型的正確性。在建模中，帶鋼采用三維實體需要消耗大量的計算時間，這是不可接受的。

2000 年J.W.Morris［25］提出:薄寬帶鋼變形是一個平面應變問題，可以忽略帶鋼厚度方向的應力和應變，采用板殼單元也能準確地仿真薄寬帶鋼的變形過程。2001 年J.W.Morris、Yoshida、Masaki 等學者將如何考慮并模擬材料包辛格效應作為首要問題。帶鋼在拉伸彎曲變形過程中帶鋼反復彎曲，材料處于拉伸、壓縮交互的循環應力狀態，材料包辛格效應不能忽略，需要在有限元仿真中采用合適的硬化法則進行模擬。對三種硬化法則下的計算結果與實驗結果進行了比較研究，發現基于混合強化準則的材料本構模型能夠更加準確地描述材料的循環應力和包辛格效應。近年來，大多國內發表的利用有限元仿真拉矯過程的文獻在建模方面沒有考慮到包辛格效應，認為帶材中間層一直處于單向拉伸作用，不用考慮包辛格效應，這樣是不妥的［19］。2002 年，Hoon Huh、Hyoung Wook Lee 等人［26-28］應用有限元對帶鋼拉伸彎曲變形過程中橫截面的應力應變規律進行了仿真研究，得出了拉伸彎曲矯直過程中帶鋼橫截面縱向應力應變分布的變化規律，描述了帶鋼延伸率的產生過程。并指出了網格大小對結果的影響。2005 年J.W.Morris 采用魯棒設計思想對帶鋼在各彎曲輥上形成的包角、帶鋼線速度、延伸率和材料屈服應力等因素進行了組合工況設計，通過仿真計算得出以上因素對拉伸彎曲矯直后帶鋼縱向翹曲、延伸率、帶鋼中心層殘余應力等矯直效果評價參數的影響強弱順序和趨勢，建立了拉伸彎曲矯直后帶鋼縱向翹曲程度的線性計算模型［29］。近兩年，國外對拉矯機的研究工作力求開發出能夠既快速又精確的拉矯機模型。2010 年L Steinwender［30］等人采用基于虛擬工作原則的建模方法，減少模型的自由度，大大減少了計算時間，通過廣泛的工業比較，驗證了這一仿真方法的可靠性。

5 展望

(1)隨著拉矯帶鋼厚度的增加，傳統解析法中的相關假設存在著明顯的不足，需要探求比較貼近實際的新的拉矯解析模型。

(2)鑒于拉矯過程的復雜性，不存在簡單的解析公式來描述整個拉矯過程，在清楚拉矯機理的前提下，有限元方法的應用是大勢所趨。因此，開發低成本的準確的有限元模型是十分必要的。它不僅可以優化生產工藝參數、評價拉矯機的拉矯能力，還可以為設計拉矯機提供技術支持。

［1］曾田長一郎.最新的板帶材矯正法［J］.塑性與加工，1976(10):853－862.

［2］Yoshisuke MISAKA.Shape correction of steel strip by tension leveler［J］.Journal of Japan Society for Technology of plasticity，1976，17:968－974.

［3］T.Sheppard.A mathematical analysis of the roller－leveling process［J］.Journal of the Institute of Metal，1969，95:225－231.

［4］T.Sheppard.Stress－strain relationships for strip－shape correction process［J］.Journal of the Institute of Metal，1971，99:223－228.

［5］T.Sheppard.On the mechanics of the tension－leveling process［J］.Journal of the Institute of Metal，1971，99:293－301.

［6］T.Sheppard.Shape correction in steel by tension leveling［J］.Sheet Metal Industry，1979(12):1149－1154.

［7］E.J.Patula.The tension－roll conformity in the tension－leveling procees［J］.Journal of the Institute of Metal，1972，101:269－277.

［8］T.X.Yu，w.Johnson.Influence of Axial Force on the Elastic－plastic Bending and Springback of a Beam［J］.Journal of Mechanical Working Technology，1982(4):31－36.

［9］劉啟森.彈塑性拉伸彎曲矯直理論及其應用［J］.重型機械，1982(4):1－11.

［10］徐守國，王繼中.帶材浪形的拉伸彎曲矯直［J］.鋼鐵，1989，7(24):25－30.

［11］肖林.金屬帶材連續拉伸彎曲矯直變形機理研究［D］.北京:北京科技大學，1999.12.

［12］李同慶.寬帶鋼拉矯機工作機理以及性能優化的研究［D］.北京:北京科技大學，1997.

［13］崔普.矯直原理與矯直機械［M］.北京:冶金工業出版社，2005.

［14］李忠富.新型酸洗帶鋼拉矯機板形矯正原理［D］.北京:北京科技大學，2004.

［15］崔甫.矯直技術與理論的新探索［M］.北京:冶金工業出版社，2010.

［16］王文廣.寬帶鋼拉伸彎曲矯直機工作機理及使用工藝研究［D］.北京:北京科技大學，2008.

［17］N.E.Thompson.New results on the theory of tension leveling［J］.Advanced Technology of Plasticity，1984(1):587－591.

［18］洪麗英.帶鋼連續機組的張緊裝置及張緊力控制［A］，94 年全國冶金設備年會論文［C］.北京:1994，34－37.

［19］鄧凱.拉矯機延伸率研究與控制系統仿真［D］.北京:北京科技大學，2005.

［20］劉琨明.金屬帶材連續拉伸彎曲矯直變形機理研究［D］.青島:青島理工大學，2000.

［21］汪建春.拉彎矯直過程中變形機理的探討［J］.武漢科技大學學報(自然科學版)，2008，31(2).

［22］王社昌.連續拉伸彎曲矯直生產工藝參數探討［J］.重型機械，1996(3):8－11.

［23］傅玉勇，李國龍，劉飛.拉伸彎曲矯直機張力與彎曲的配置關系研究［J］.現代制造工程，2006(7):61－64.

［24］劉妍.基于改善板形的帶材拉伸彎曲矯直理論研究及其仿真［D］.秦皇島:燕山大學，2007.

［25］Morris J W，Hardy S J，Lees A W，Thomas J T.Formation of residual stresses owing to tension leveling of cold rolled strip［J］.Ironmaking and Steelmaking，2001，28(1):44－52.

［26］E.Doege，R.Menz，S.Huinink.Analysis of the levelling process based upon an analytic forming model［J］.Annals of the CIRP，2002，51:191－194.

［27］Hoon Huh，Hyoung Wook Lee.The parametric process design of tension levelling with an elasto－plastic finite element method［J］.Journal of Material Processing Technology，2001，113:714－719.

［28］Morris J W，Hardy S J，Thomas J T.Some fundamental considerations for the control of residual flatness in tension leveling［J］.Journal of Materials Processing Technology，2002，120:385－396.

［29］Morris J W，Hardy S J，Thomas J T.Effects of tension leveling process parameters on cold rolled strip characteristics using a designed factorial analysis approach［J］.Ironmaking and Steelmaking，2005，132(5):443－448.

［30］L Steinwender，A KainzK Krimpelst?tter K Zeman Computational analysis of the curvature distribution and power losses of metal strip in tension levelers［J］Materials Science and Engineering 2010 (10):1－10.