趨勢面分析法在預(yù)測導(dǎo)水裂隙帶高度中的應(yīng)用

陳 凱 嚴(yán)桂鳳 文 江 賀根義

（1.中國礦業(yè)大學(xué)資源與地球科學(xué)學(xué)院，江蘇省徐州市，221116；2.中國礦業(yè)大學(xué)礦業(yè)工程學(xué)院，江蘇省徐州市，221116；3.新疆地礦局第二水文工程地質(zhì)大隊，新疆維吾爾自治區(qū)昌吉市，831100）

近年來，隨著我國礦井開采水平的不斷延伸，在煤炭資源開采過程中會不同程度受到近含水層和地表水體的威脅，然而是否會發(fā)生煤層頂板突水，其關(guān)鍵因素在于確定導(dǎo)水裂隙帶發(fā)育的最大高度。因此，對導(dǎo)水裂隙帶發(fā)育高度的研究在煤礦頂板防治水方面具有重要的實用意義和經(jīng)濟(jì)意義。

現(xiàn)階段，對導(dǎo)水裂隙帶發(fā)育高度的預(yù)測方法主要有規(guī)程公式經(jīng)驗法、相似材料模型試驗、數(shù)值模擬以及井下實測等。此外，隨著軟科學(xué)決策方法的發(fā)展，一些學(xué)者將人工神經(jīng)網(wǎng)絡(luò)法 （ANN）、支持向量機(jī)法 （SVM）等應(yīng)用到導(dǎo)水裂隙帶發(fā)育高度的預(yù)測中，均取得了一些重要的研究成果。然而這些預(yù)測方法在理論計算和實踐中都存在一定的缺陷，基于此，本文提出了利用趨勢面法來預(yù)測導(dǎo)水裂隙帶發(fā)育高度。

1 趨勢面分析過程

1.1 基本理論

趨勢面分析法是以多元回歸分析理論為基礎(chǔ)的一種統(tǒng)計方法，運(yùn)用最小二乘法將離散變量擬合成一個光滑的數(shù)學(xué)曲面，用以表述因變量與自變量之間的關(guān)系及變化趨勢。多元線性回歸分析也稱復(fù)線性回歸分析，它是一元線性回歸分析或簡單線性回歸分析的推廣，它研究的是一組自變量如何直接影響一個因變量。這里的自變量指的是獨(dú)立自由變化的變量，一般用x 表示，因變量指的是非獨(dú)立、受其他變量影響的變量，一般用y 表示。

1.2 影響因子與實測數(shù)據(jù)

在近含水層和地表水體下采煤過程中，影響導(dǎo)水裂隙帶發(fā)育高度的因素有很多，根據(jù)現(xiàn)場實測，并參考相關(guān)研究成果，經(jīng)過綜合分析后，初步選定采高、硬巖巖性比例系數(shù)、斜長、采深和推進(jìn)速度5個影響因子作為導(dǎo)水裂隙帶發(fā)育高度的關(guān)鍵因素。在這5個參數(shù)指標(biāo)中，引用了文獻(xiàn)中的硬巖巖性比例系數(shù)這個指標(biāo)，硬巖巖性比例系數(shù)是指煤層頂板以上統(tǒng)計高度范圍內(nèi) （導(dǎo)水裂隙帶高度），硬巖的統(tǒng)計高度與煤厚的比值，參與統(tǒng)計的硬巖主要是指細(xì)砂巖、中砂巖、粗砂巖，比值計算式：

式中：M——煤厚，m；

∑h——估算的導(dǎo)水裂隙帶高度范圍內(nèi)的硬巖巖層統(tǒng)計的累計厚度 （根據(jù)地方預(yù)計導(dǎo)水裂隙帶高度的經(jīng)驗來考慮取多少倍的煤厚，一般為15～20倍煤厚），m。

該指標(biāo)的提出，既可以反映煤層頂板強(qiáng)度類型，也可以反映上覆巖層的巖性組合關(guān)系，避免了現(xiàn)行規(guī)范中對頂板類型的劃分不確定的問題。

以20個工作面實測到的導(dǎo)水裂隙帶發(fā)育高度和影響因子作為趨勢面分析的原始數(shù)據(jù)，見表1。

表1 導(dǎo)水裂隙帶高度實測值及相關(guān)影響因素數(shù)據(jù)

1.3 運(yùn)行結(jié)果

以表1中的實測數(shù)據(jù)為基礎(chǔ)，利用SPSS統(tǒng)計軟件對導(dǎo)水裂隙帶發(fā)育高度與采高、硬巖巖性比例系數(shù)、斜長、采深和推進(jìn)速度之間的相關(guān)性進(jìn)行分析。

1.3.1 趨勢面模型的顯著性檢驗

從SPSS輸出結(jié)果中可以看到趨勢面模型的方差分析表，如表2所示。在實際應(yīng)用中，通常使用復(fù)相關(guān)系數(shù)R 來檢驗趨勢面模型的顯著性。即：

PD-1抑制劑是程序性細(xì)胞死亡蛋白-1(programmed death-1,PD-1)及其配體(PD-L1)抑制劑，是免疫哨點單抗藥物。主要在激活的T細(xì)胞和B細(xì)胞中表達(dá)，功能是抑制細(xì)胞的激活，這是免疫系統(tǒng)的一種正常的自穩(wěn)機(jī)制。但是，腫瘤微環(huán)境會誘導(dǎo)浸潤的T細(xì)胞高表達(dá)PD-1分子，腫瘤細(xì)胞會高表達(dá)PD-1的配體PD-L1和PD-L2，導(dǎo)致腫瘤微環(huán)境中PD-1通路持續(xù)激活，T細(xì)胞功能被限制，無法殺傷腫瘤細(xì)胞。PD-1的抗體可以阻斷這一通路，部分恢復(fù)T細(xì)胞的功能，使這些細(xì)胞能夠繼續(xù)殺傷腫瘤細(xì)胞[1]。近年來，我們對3例腦膠質(zhì)瘤患者使用PD-1抑制劑進(jìn)行免疫治療，經(jīng)精心護(hù)理，效果滿意。現(xiàn)報告如下。

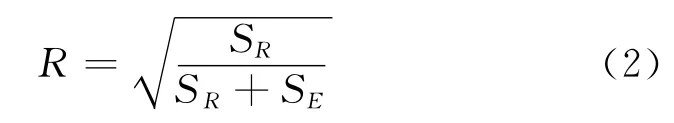
式中：R——復(fù)相關(guān)系數(shù)；

SR——回歸平方和；

SE——?dú)埐钇椒胶汀?/p>

由公式 （2）可知，復(fù)相關(guān)系數(shù)的取值范圍為0≤R≤1。R 越接近1表明SE越小，回歸模型擬合程度越好。

根據(jù)SPSS輸出的趨勢面方程的復(fù)相關(guān)系數(shù)達(dá)到了0.97，預(yù)測值的標(biāo)準(zhǔn)差為3.12041，表明該預(yù)測模型是極顯著的，具有統(tǒng)計學(xué)意義。此外，從表2中看出差異性顯著的檢驗值小于0.001，拒絕原假設(shè)，可以認(rèn)為導(dǎo)水裂隙帶發(fā)育高度和5個影響因子間有明顯的線性關(guān)系。因此，該趨勢面模型可以用于預(yù)測導(dǎo)水裂隙帶發(fā)育高度的計算。

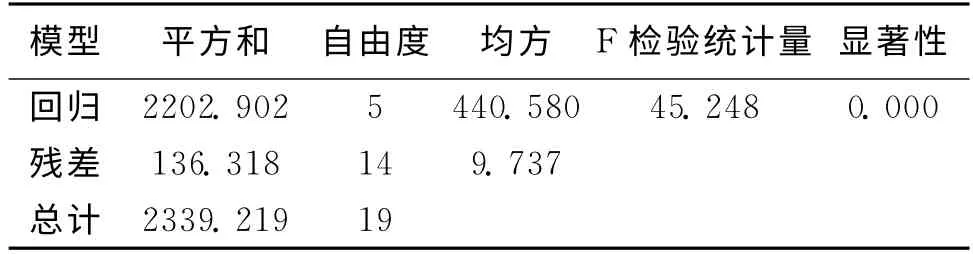
表2 方差分析表

1.3.2 趨勢面模型的建立

根據(jù)SPSS輸出的結(jié)果，可以得到趨勢面模型的回歸系數(shù)，如表3所示。

表3 趨勢面模型的參數(shù)估計表

根據(jù)表3中非標(biāo)準(zhǔn)化的回歸系數(shù)可以建立趨勢面模型：

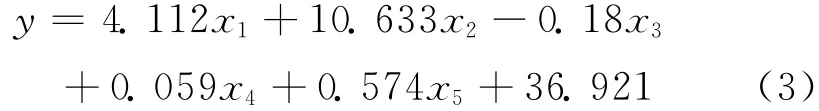
式中：y——導(dǎo)水裂隙帶發(fā)育高度；

x1、x2、x3、x4、x5——分別表示采高、硬巖巖性比系數(shù)、斜長、采深和推進(jìn)速度。

此外，還可以根據(jù)表3中標(biāo)準(zhǔn)系數(shù)的絕對值大小來判別在采高、硬巖巖性比例系數(shù)、斜長、采深和推進(jìn)速度這5個影響因子中哪個對因子導(dǎo)水高度預(yù)測的貢獻(xiàn)最大，從標(biāo)準(zhǔn)系數(shù)可以看出采高對導(dǎo)水高度的影響最大。

1.3.3 趨勢面模型的預(yù)測效果分析

根據(jù)建立的趨勢面預(yù)測模型，把表1中的實測數(shù)據(jù)代入式 （3），可以計算得到預(yù)測導(dǎo)水裂隙帶的發(fā)育高度，具體誤差結(jié)果如表4所示。從該預(yù)測模型計算出的預(yù)測值和實測值之間的誤差可以看出，應(yīng)用趨勢面方程所預(yù)測的發(fā)育高度和實際發(fā)育高度的誤差不是很大，在0.17%～5.39%之間。因此，應(yīng)用SPSS軟件建立的趨勢面分析預(yù)測模型具有較高的精度和可行性。此外，為使該預(yù)測模型更加有效，應(yīng)在后續(xù)的工作中不斷補(bǔ)充和完善學(xué)習(xí)樣本的數(shù)量，使其更加貼近實際，為礦井的安全生產(chǎn)提供技術(shù)支持。

表4 導(dǎo)水裂隙帶高度預(yù)測值與實測值之間的相對誤差統(tǒng)計表

2 工程應(yīng)用

將建立的趨勢面模型預(yù)測關(guān)系式應(yīng)用于兗礦興隆莊煤礦2303-2-3放7工作面，預(yù)測煤層頂板導(dǎo)水裂隙帶的高度。該工作面煤層埋深312m，開采厚度為5.3m，工作面斜長為145.7m，工作面每天推進(jìn)3.8m，又根據(jù)本礦區(qū)開采經(jīng)驗和相關(guān)鉆孔柱狀圖計算得到硬巖巖性比例系數(shù)為0.24。

將以上參數(shù)代入式 （3），計算得到預(yù)計的導(dǎo)水裂隙帶高度為55.63 m，經(jīng)過現(xiàn)場實測的高度為54.5m。可以看出，預(yù)測值和實測值相差很小，相對誤差為1.13%。由此表明本文建立的導(dǎo)水高度趨勢面預(yù)測模型比較符合實際，為煤層頂板防治水提供了科學(xué)依據(jù)。

3 結(jié)論

（1）利用SPSS軟件得出導(dǎo)水裂隙帶高度與采高、硬巖巖性比例系數(shù)、斜長、采深和推進(jìn)速度之間有較好的相關(guān)性，并建立了趨勢面分析預(yù)測模型為下一步問題的探討做鋪墊。

（2）研究結(jié)果表明，選取采高、硬巖巖性比例系數(shù)、斜長、采深和推進(jìn)速度5個影響因子，運(yùn)用趨勢面分析理論進(jìn)行導(dǎo)水裂隙帶發(fā)育高度的預(yù)測是可行的，其預(yù)測結(jié)果具有較高的精度，為近含水層和地表水體下安全采煤提供了科學(xué)依據(jù)。

（3）根據(jù)標(biāo)準(zhǔn)系數(shù)的絕對值可以看出，在5個影響因子中采高對導(dǎo)水裂隙帶發(fā)育的高度貢獻(xiàn)最大。

（4）從計算結(jié)果可知，該函數(shù)模型的精度與適應(yīng)性和學(xué)習(xí)樣本的多少有密切關(guān)系，因此，在后續(xù)工作中應(yīng)不斷將新觀測到的數(shù)據(jù)加入函數(shù)模型，對函數(shù)模型進(jìn)行修正，以更好地發(fā)揮其實用價值。

［1］ 王秀蘭.礦井水防治 ［M］.徐州：中國礦業(yè)大學(xué)出版社，2010

［2］ 張衛(wèi)，于仲.導(dǎo)水裂隙帶高度探測方法概論 ［J］.煤炭技術(shù)，2011 （8）

［3］ 呂霽，孫世國.特厚煤層綜放開采上覆巖層導(dǎo)水裂隙帶高度研究 ［J］.中國煤炭，2011 （1）

［4］ 吳廣竹，徐智敏.基于BP神經(jīng)網(wǎng)絡(luò)的導(dǎo)水裂隙帶高度預(yù)測研究 ［J］.能源技術(shù)與管理，2008 （8）

［5］ 馬亞杰，李建民，郭立穩(wěn)等.基于ANN 的煤層頂板導(dǎo)水?dāng)嗔褞Ц叨阮A(yù)測 ［J］.煤炭學(xué)報，2007 （9）

［6］ 王正帥，鄧喀中，譚志祥.導(dǎo)水裂縫帶高度預(yù)測的模糊支持向量機(jī)模型 ［J］.煤炭學(xué)報，2011 （8）

［7］ 楊永國.數(shù)學(xué)地質(zhì) ［M］.徐州：中國礦業(yè)大學(xué)出版社，2010

［8］ 胡小娟，李文平，曹丁濤等.綜采導(dǎo)水裂隙帶多因素影響指標(biāo)研究與高度預(yù)計 ［J］.煤炭學(xué)報，2012（4）