基于混淆器的安全對稱密碼方案*

袁 征，龔高翔

(1.北京電子科技學院，北京 100070； 2.西安電子科技大學 通信工程學院， 陜西 西安 710071)

密碼學中的對稱密碼算法具有速度快、容易實現、安全強度高、易于同步等特點，被廣泛應用在互聯網中。但是對稱密碼算法也存在密鑰更換困難、用同一密鑰加解密容易給敵手提供破解密鑰的信息和時間等缺陷。本文利用混淆器設計了一個對稱密碼方案。所謂混淆器就是輸入一個程序(例如，圖林機，或者回路)[1]，輸出一個與原始程序功能相同的新的程序的(有效的)算法，且輸出的程序還具有“難以識別性”。此概念要求混淆器表現的像一個“黑盒”。由于具有多比特輸出的點函數混淆器具有對稱密碼的特點和其它優(yōu)點[2]，本文利用多比特輸出的點函數混淆器構造的加密方案不僅具有很高的安全性，而且實現了“動態(tài)”密鑰[3]。

1 虛擬黑盒混淆與點函數混淆器

首先介紹混淆中最基礎的概念——虛擬黑盒混淆[4]，然后介紹具有多比特輸出點函數混淆器[2]。

1.1 虛擬黑盒混淆

一個算法O，其輸入為族c中的一個回路，輸出一個新的回路，被稱為族c的黑盒混淆器。如果算法O有如下三個特性，就被定義為虛擬黑盒混淆：

1)保留功能性：存在一個可以忽略的函數neg(n)，使得對于任意輸入長度n和每一個C∈Cn，有：

Pr[?x∈{0,1}n:O(C)(x)≠C(x)]≤neg(n)

(1)

式(1)是在隨機Oracle(預言機)和O的coin(投硬幣)上的概率。

2)多項式遞減性：存在一個多項式p(n)，使得對于所有有限多的輸入長度和每一個C∈Cn,混淆器O僅能把C擴大p:|O(C)|≤p(|C|)的一個因子。

3)虛擬黑盒特性(VBB)：對于任意多項式大小回路敵手A，存在一個多項式大小模擬器回路S和一個可以忽略的函數neg(n)，使得對于每個輸入長度為n和每個C∈Cn，有：

|Pr[A(O(C)) =1]-Pr[Sc(1n) =1]|≤neg(n)

(2)

式(2)是在敵手、模擬器和混淆器的coin(投硬幣)上的概率。

虛擬黑盒混淆器O是運行在多項式時間內的，所以是有效的[5]。

1.2 具有多比特輸出的點函數混淆

設I(k,m):{0,1}*∪{⊥}→{0,1}*∪⊥表示為函數：

(3)

若給定密鑰k，式(3)輸出消息m，否則輸出⊥。設Ι={I(k,m)|k,m∈{0,1}*}為所有這樣函數的族，被稱為具有多比特輸出點函數族，簡稱多比特點函數(MBPF)。

定義1(具有多比特輸出的點函數混淆MBPFO)[6]一個多比特點函數(MBPF)混淆器是一個概率多項式時間算法O，其輸入(k,m)值，描述為一個函數I(k,m)∈Ι，輸出一個回路C，記為O(I(k,m))。但是這里一直假設O把k和m作為描繪的輸入。滿足如下條件：

1)正確性：對于所有的(k,m)∈{0,1}*， |k|=n,|m|=poly(n)，所有的x∈{0,1}n，滿足：

Pr[C(x)≠I(k,m)(x)|C←O(I(k,m))]≤negl(n)

(4)

式(4)是混淆器算法的隨機性上的概率。

2)多項式遞減性：對于任意的k,m，回路C=O(I(k,m))的大小是在|k|+|m|上的多項式。

3)熵安全性：如果對于任意有1比特輸出的概率多項式時間敵手，任意多項式l(.)，存在一個概率多項式時間模擬器S，使得對于所有的聯合分布{Xn,Yn}n∈N，(其中Xn∈{0,1}n，Yn∈{0,1}l(n)，H∞(Xn)≥α(n))，滿足式(5)，就說該方案具有α(n)-熵安全性：

|Pr[A(O(I(k,m)))=1]-

Pr[SI(k,m)l(.)(1n)=1]|≤negl(n)

(5)

式(5)是(k,m)←(Xn,Yn)的隨機性、混淆器O的隨機性和A,S的隨機性上的概率。

如果對于所有的α(n)∈ω(log(n))，方案具有α(n)-熵安全，就說該方案具有完全熵安全性。完全熵安全性暗示著虛擬黑盒特性(VBB)，但反過來不一定。

2 構建一個基于混淆器的安全對稱密碼方案

本部分首先介紹具有多比特輸出點函數混淆器與對稱密碼之間的關系。把一個公共私鑰和一個隨機密鑰(公開的)作為輸入，通過一個敏感函數產生“動態(tài)”密鑰，然后構造出一個“隨機”的多比特輸出點函數混淆器，此混淆器具有“動態(tài)”密鑰的對稱密碼功能。

2.1 具有多比特輸出點函數混淆器(MBPFO)與對稱密碼之間的關系

此部分介紹了具有多比特輸出點函數混淆器暗示了一個非常強對稱密碼類型(也叫著數字鎖[7])。

定義2(錯誤密鑰檢測[8]) 如果對于所有的k≠k′∈{0,1}n，所有m∈{0,1}poly(n)，有Pr[Deck′(Enck(m))≠⊥]≤neg(n)，就說這個加密方案滿足錯誤密鑰檢測。

根據文獻[8]，有如下定理。

定理1 令α(n)∈w{log(n)}，對于α(n)-弱密鑰，存在滿足錯誤密鑰檢測的語義安全加密方案的充分必要條件是對于消息獨立，存在α(n)-熵安全MBPF混淆器。用“完全”代替“α(n)”，該定理也成立。

用定理1構造(MBPFO到對稱密碼)。設O為一個消息獨立的MBPF混淆器，定義(概率的)加密算法Enck(m)=O(I(k,m))和解密算法Deck(c)=C(k)，其中C被理解為一個多比特輸出點回路(MBPC)，k是從密鑰Dn域中選取的一個密鑰。

這里“MBPFO”和“對稱密碼”的概念是平等的：首先它們滿足相同的正確性，特別是給定密鑰，加密方案允許恢復消息；同樣式(3)中給定k，MBPFO允許恢復x。其次，它們有相似的保密要求，除非給定k，式(3)的函數I(k,m)(x)混淆隱藏了特殊的輸出m；同樣除非敵手擁有密鑰，對稱密碼隱藏了消息。但是，二者的不同是MBPFO的定義域是所有可能輸入的k，而對稱密碼不能定義在錯誤密鑰上，換句話說，至少在概念上認為MBPFO為對稱密碼的特殊形式，通過解密算法，錯誤密鑰被迅速檢測出來。

2.2 基于混淆器的安全對稱密碼方案

與以前的對稱密碼相比，我們的對稱密碼方案的加密算法被一個具有對稱密碼功能的多比特輸出的點函數混淆器所替代。而我們的加密方案的密鑰是“動態(tài)”的，改變了以前對稱密碼方案中密鑰的不變性。在敏感函數作用下產生的“動態(tài)”密鑰，增加了我們的對稱密碼方案的安全性。

用戶甲和乙協商確定多比特輸出點函數混淆算法O、私鑰k1和敏感函數Η，具體對稱密碼方案如下：

1)用戶甲：任意選擇一個公開的密鑰k2，并計算k=Η(k1,k2)；

2)用戶甲：用具有對稱密碼功能的多比特點函數混淆算法O和密鑰k，對需要混淆加密的明文m進行混淆加密，得到混淆后的密文c=Enck(m)=O(I(k,m))；

3)用戶甲：在公共信道上，把k2和c同時傳送給用戶乙；

4)用戶乙：接收到密文c和密鑰k2后，根據私鑰k1和k2，計算k=Η(k1,k2)；

5)用戶乙：用以上的解密算法和k，對密文c進行解密，得到明文m=Deck(c)=C(k)。

以上方案中，私鑰k1需要通過秘密通道交換協商，密鑰k2在混淆加密時隨機選擇。k1和k2的選擇相互無關，無論給出多少個k2，都不會推出k1；k1和k2對于Η(敏感函數)的敏感性，k1和k2的細微變化都會引起k=Η(k1,k2)的明顯變化，使產生的結果具有很好的擴散性與混淆性。

3 基于混淆器的對稱密碼方案的性能分析

3.1 對稱密碼方案的正確性

定理2 基于MBPFO的對稱密碼方案是正確的。

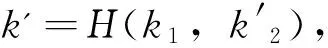
因為

Deck'(c)=C(k')，Enck(m)=O(I(k,m))

(6)

任取m∈{0,1}poly(n)，有：

m=Deck'(Enck(m))=Deck'(O(I(k,m)))

(7)

因為我們基于的多比特輸出的點函數混淆器(MBPFO)是完全熵安全的，所以我們的對稱密碼方案滿足錯誤密鑰檢測功能，即：若k≠k′∈{0,1}n，則：pr[Deck′(Enck(m))≠⊥]≤neg(n)，

所以，當且僅當k=k′時，m=Deck'(Enck(m))=Deck'(O(I(k,m)))=C(k)=m，正確。

3.2 “動態(tài)”密鑰的安全性分析

“一次一密” 密碼體制的密鑰是隨機產生的，其明文、密文和密鑰三者是相互獨立的，敵手不能從密文中獲得關于明文或者密鑰的任何消息，即使敵手獲得一些密文及所對應的明文，也只能得到相應的密鑰，而不能得到其它密文對應的明文或者密鑰。因此“一次一密”的密碼體制在理論上被認為是絕對安全的[10]。

我們的對稱密碼方案雖然與傳統的“一次一密” 密碼體制不同，但是通過隨機密鑰k2，可以實現類似于“隨機”的密鑰k。我們的對稱密碼方案還解決了傳統“一次一密”密碼體制中密鑰管理困難問題。實際上，如果函數Η滿足對私鑰k1和隨機密鑰k2的單射性質，也就是：

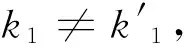
(8)

我們的對稱密碼方案的安全性最高。

由于敏感函數Η具有很強的敏感性，一般從混沌系統中選取[11]。在混沌系統中的特性之一就是對初值的敏感依賴性。這樣Η對私鑰k1和動態(tài)密鑰k2是敏感的，k1或k2的細微變化，k=Η(k1,k2)都會產生巨大的變化。這正如洛倫茲在一次演講中生動地指出：一只蝴蝶在巴西煽動翅膀，就有可能在美國的德克薩斯州引起一場風暴。由于密鑰在每次加密都在不斷地變化，從而使得密文與明文之間具有很高的非線性特性，從而提高了對稱密碼方案的安全性能。

敏感函數對初始密鑰和隨機密鑰敏感性的實驗分析。我們從敏感性很好的混沌系統中選取一個敏感函數H，敏感函數H定義如下：

H(k1,k2)=mod(abs(round(Fk1.T(t)×k2)),256)

(9)

其中，k1為敏感函數的初始密鑰；k2為隨機密鑰；T為一種采樣規(guī)定；Fk1,T(t)為采樣后的混沌信號；round是四舍五入運算，abs是取絕對值；mod是取余。敏感函數的輸出值是在[0,255]上的整數序列。

1)敏感函數對k1的敏感性分析：令Hi(k1,k2)為H(k1,k2)的第i個元素、Δk1為k1的誤差，敏感函數H產生一個長度為t的序列

s={s(1),...,s(t)}：s(i)=

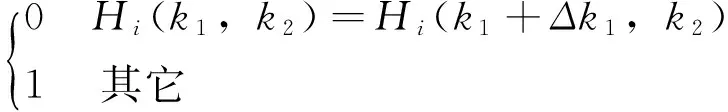
(10)

顯然，密鑰序列s表明了H(k1+Δk1,k2)和H(k1,k2)之間對應元素的變動情況。

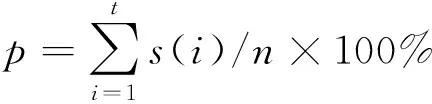
表1 敏感函數H對初始密鑰k1的敏感性 Table 1 Sensitivity of sensitive function H on initial key k1

由此實驗可知，初始密鑰k1的細微變化，敏感函數產生的密鑰序列都會發(fā)生99.5%的變化。

2)同樣，敏感函數對于隨機密鑰k2的敏感性分析也可以采用以上的p作為評估標準，只是序列定義成為：

(11)

通過實驗，同樣也可以得到，隨機密鑰k2的細微變化，序列密鑰都會發(fā)生99.5%以上的很大的變化。

綜上所述，從混沌系統選取的敏感函數H對密鑰k1和k2是非常敏感的，所以方案的安全性很高。

3.3 對稱密碼方案的安全性

定理3 如果O是一個滿足完全熵的MBPF混淆器，則O也滿足虛擬黑盒混淆。

說明此定理的具體證明思路方法是改編的條件到多比特集[9]，證明思路分為三步：

1)如果一個混淆器O滿足完全安全，則其滿足分布的不可辨別性。

2)如果一個混淆器O滿足分布的不可辨別性，則其滿足Oracle(預言機)不可辨別性。

3)如果一個混淆器O滿足Oracle(預言機)不可辨別性，則其滿足虛擬黑盒性能。

定理4 基于滿足完全熵的MBPFO的對稱密碼方案是安全的。

證明對稱密碼方案安全性主要依賴于滿足完全熵的多比特輸出的點函數混淆器(MBPFO)的安全性和“動態(tài)”密鑰的安全性。

根據前面定理3，我們對稱密碼方案基于的滿足完全熵的MBPFO，也滿足虛擬黑盒混淆，是安全的混淆器。

根據前面定理1，對于獨立消息，存在α(n)-熵安全的MBPFO，也存在有錯誤密鑰檢測的語義安全加密方案。令C為多比特輸出點回路(MBPC)，?k∈Dn，由該多比特輸出的點函數混淆器O到對稱密碼的表示是：

Enck(m)=O(I(k,m)),和Deck(c)=C(k)

(12)

根據文獻[8]，有以下結論：①對于α(n)-弱密鑰，存在CPA安全的、具有“錯誤密鑰檢測性”的對稱密碼方案的充分必要條件是：對于獨立消息，存在α(n)-熵安全的、自我可組合的MBPF混淆器；②對于α(n)-弱密鑰，存在密鑰獨立消息(KDM)的、具有“錯誤密鑰檢測性”的語義安全對稱密碼方案的充分必要條件是：對于獨立消息的標準概念，存在α(n)-熵安全的MBPF混淆器。

另外，我們所基于的混淆器還有如下優(yōu)點：①混淆后函數的難以識別，這給敵手攻擊增加難度，此性質可以增加安全性；②該混淆器可以同時對多個回路進行串行作用，大大提高了混淆器的運行速度。③在文[12]中，多比特輸出的點函數混淆器暗示非常強的對稱密碼，對于密鑰依賴消息和隨機弱密鑰是安全的。④該混淆器包含弱密鑰抵抗，以及具有密鑰依賴消息安全的[13]。

綜上所述，我們的基于滿足完全熵的MBPFO的對稱密碼方案選用的加密算法是具有很高安全性的多比特輸出的點函數混淆器，混淆本身還有結果難以識別等優(yōu)點；而只要密鑰k1和k2有細微變化，用敏感函數H得到的“動態(tài)”密鑰k都會產生99.5%以上的變化，所以我們的方案的安全性很高。

4 結 語

滿足完全熵的多比特輸出的點函數混淆器(MBPFO)等同于一個具有“錯誤密鑰檢測性”的語義安全的對稱密碼功能，因此本文提出了一個基于該混淆器的對稱密碼方案，方案具有虛擬黑盒性能，保證了混淆的安全性，可以抵抗各種混淆攻擊。用敏感函數產生該對稱密碼方案的“動態(tài)”密鑰， 敏感函數的輸入是私鑰k1(混沌系統的初始條件)和隨機密鑰k2，k1和k2中任意一個發(fā)生微小的變化，由敏感函數產生的“動態(tài)”密鑰k將發(fā)生99.5%以上的改變。加密者通過改變k2使得每次加密都用不同的密鑰k，從而實現類似“一次一密”的密碼體制功能，使得我們對稱密碼方案從密鑰和算法兩方面更加安全。

參考文獻：

[1] BOAZ B, ODED G, RUSSELL I, et al. On the (im)possibility of obfuscating program[M]. CRYPTO,2001: 1-18.

[2] CANETTI R,DAKDOUK R R. Obfuscating point functions with multibit output[C]∥EUROCRYPT, Lecture Notes in Computer Science, 2008,4965:489-508.

[3] 陳魯生，沈世鎰. 現代密碼學[M]. 北京：科學出版社,2002:36.

[4] GOLDWASSER S, ROTHBLUM G N.On best-possible obfuscation[C]∥Vadhan, S.P.ed. TCC 2007. LNCS, Springer, Heidelberg,2007,4392:194-213.

[5] 史揚.曹立明.王小平 混淆算法研究綜述[J].同濟大學學報:自然科學版,2005(6):813-819.

[6] NIR B,RAN C. On strong simulation and composable point obfuscation[C]∥CRYPTO, advances in Cryptology-CRYPTO 2010, 30th Annual Cryptology conference, Santa Barbara,CA,USA, August 15-19,2010. Proceedings,2010:520-537.

[7] NIR B,OMER P. Point obfuscation and 3-round zero-knowledge[EB/OL].(2011-09-21)[2012-03-28].http://eprint.iacr.org.

[8] CANETTI R, KALAI Y T, VARIA M. On symmetric encryption and point obfuscation[C]∥Micciancio, D. (ed.) TCC 2010. LNCS,Springer, Heidelberg,2010,5978:52-71.

[9] CANETTI R. Towards realizing random oracles: Hash functions that hide all partial information[C]∥CRYPTO,Lecture Notes in Computer Science, Springer, 1997,1294:455-469.

[10] SHANNON C E. Communication theory of secrecy systems[J]. Bell Systems Technical Journal, 1949,28:656-715.

[11] 廖曉峰，肖迪，陳勇,等.混沌密碼學原理及其應用[M]. 北京：科學出版社, 2009:2-18.

[12] BITANSKY N, CANETTI R. On strong simulation and composable point obfuscation[EB/OL].(2010-07-25)[2012-03-28]. http://eprint.iacr.org.

[13] HAITNER I,HOLENSTEIN T. On the (im)possibility of key dependent encryption[C]∥TCC, 2009:202-219.