全并聯直供式系統并聯方式研究

杜 川 王希文

（四川省建筑設計院，成都 610031）

隨著國民經濟和對外貿易的日漸增長，對鐵路運量的要求也持續提高，載運量的不斷增加和列車運行速度的提高使得牽引網負荷電流和網絡損耗增大，上下行牽引網電流分布不均更加嚴重，從而影響到電力機車的正常運行和鐵路運輸的經濟性[1]。

提高電氣化鐵路運能這一問題可以從兩方面入手：一方面大力發展運載能力強的高速鐵路，另一方面則對既有線路進行擴能改造[2]。目前國內的高速鐵路主要采用AT供電方式[3]，而在一些山區的電氣化鐵路中直供式全并聯方式已經相繼得到應用。為了更充分的利用牽引網具備的載流能力，本文即從牽引網載流能力的角度出發，對全并聯方式進行分析。

1 帶回流線的全并聯直供牽引網電流分布

為了對牽引網的載流能力進行分析，首先需要知道牽引網中各電流的分布情況。不失一般性，以圖 1所示帶回流線的復線全并聯直供牽引網電流分布作為后續的分析模型。為了方便分析，我們假設只有上行有機車負荷，而下行無機車負荷，鋼軌對地漏導為零，忽略導線的分布電容以及橫向連接線的阻抗，并認為所有導體都為均質導體且對地絕緣[5]。

本文主要考慮接觸網的電流分布。如圖1所示，通過上行和下行的接觸線回路、機車受流點以及并聯區末端廣義節點可得以下方程。

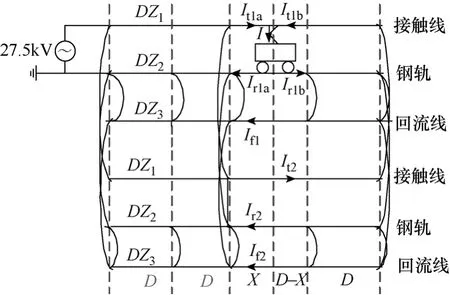
圖1 帶回流線的復線全并聯直供牽引網電流分布示意圖

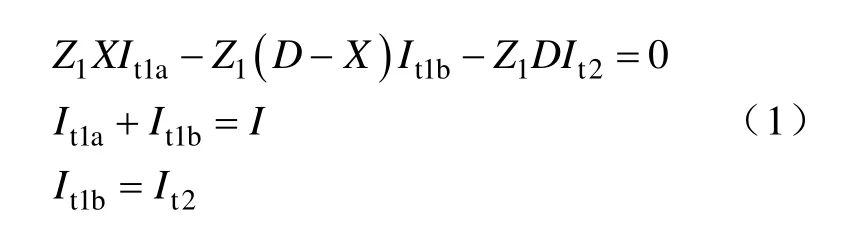
當機車取流I為已知時，可得到接觸網中電流分布如下：

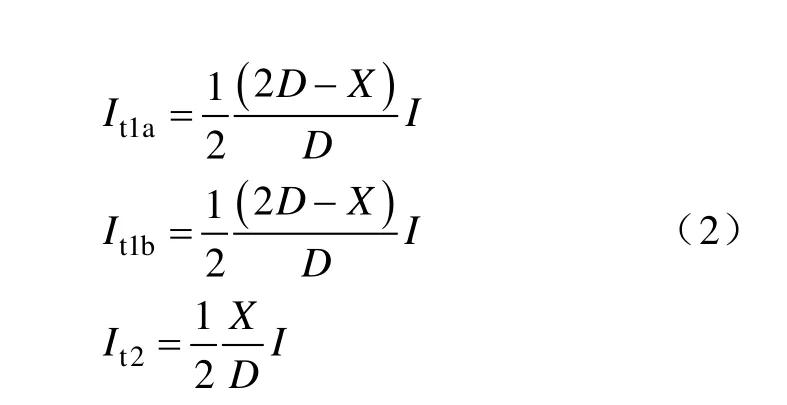
不同的全并聯方案對牽引網載流能力需求的改善是不一樣的，我們先分析牽引網中部僅有一次并聯的情況，其運行簡化示意圖如圖2所示。

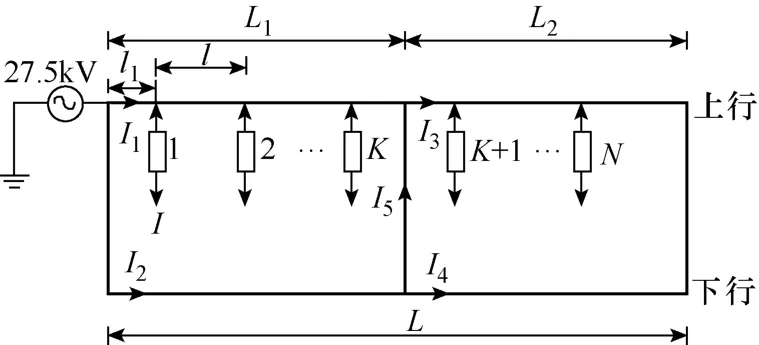
圖2 牽引網中部并聯一次的運行簡化示意圖

設并聯點距牽引變電所的長度為L1，距末端的長度為L2，供電臂長為L，上行總共有N列機車取流，其中運行在并聯點以前的機車有K列，追蹤間隔為l，第一列機車距牽引變所為l1，I1、I2、I3、I4分別為上下行各并聯區間流過的總電流，I5為橫連線上流過的總電流。由式（2）不難知道，單車運行時It1a即為機車從上行接觸網取得的電流，It1b即為機車從下行接觸網取得的電流，等于It2，D為并聯區間的長度，這里取L1或L2，由追蹤間隔可以表示任意一列機車K的位置為l1+(K?1)l。這樣即可得到各個電流的大小。

下行第一個并聯區間的總電流可表示為

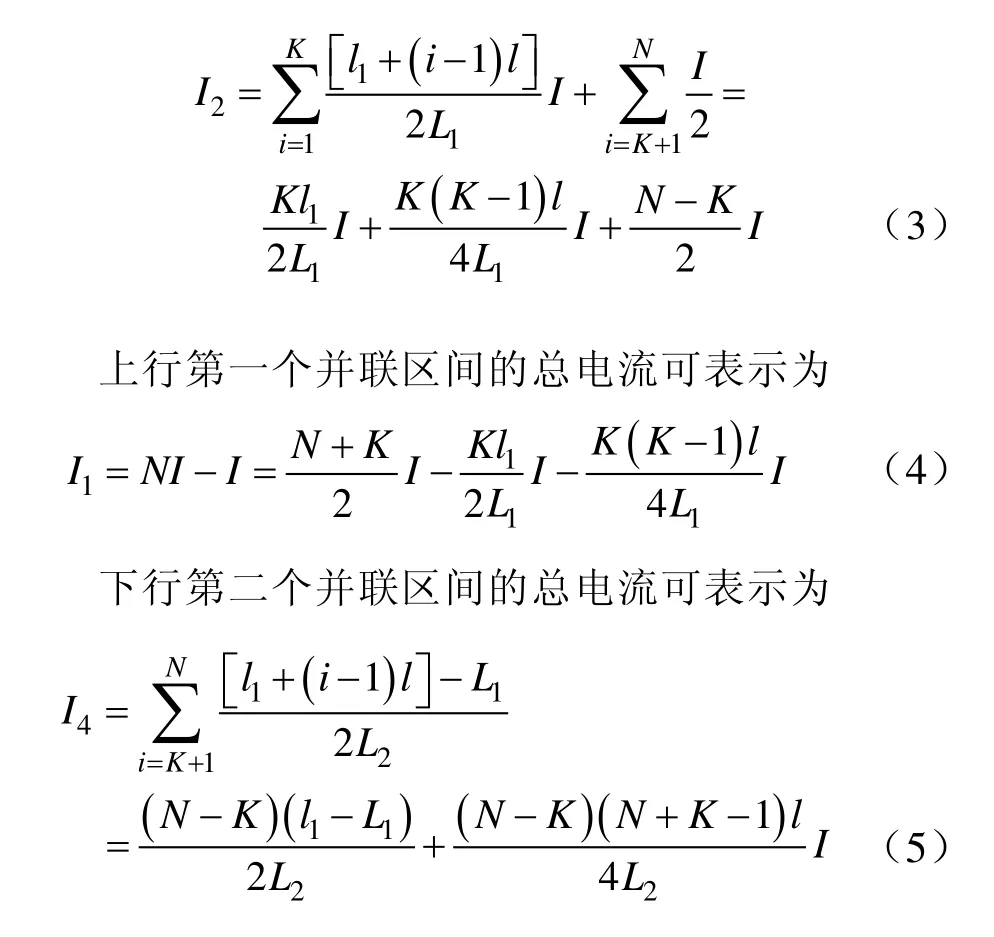
若并聯區間長度是追蹤間隔的整數倍時，即存在關系L1=Kl，L2=(N?K)l，上面各個電流即可化簡為

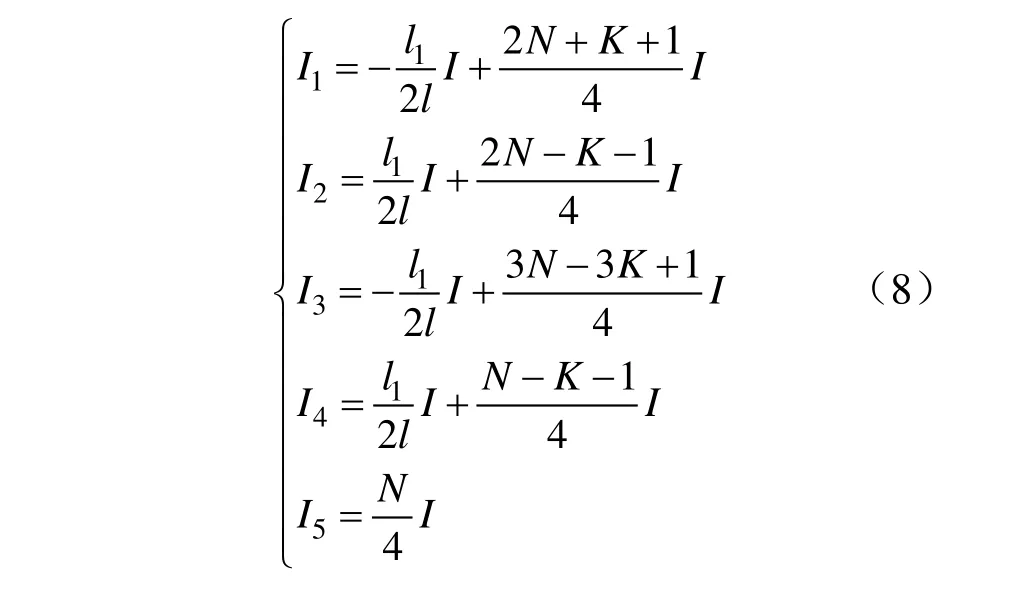
如此以來，只要知道了追蹤間隔以及第一列機車的位置，即可得到牽引網的載流需求。下面通過對不同的情況進行仿真，從而分析出一般規律。

2 仿真分析

本文利用Matlab/Simulink仿真軟件，結合實際牽引網供電系統進行仿真。假設供電臂長度為24km；選擇交—直—交機車作為負荷模型，其單車功率為 5MVA，功率因數 0.99。本文分三種情況進行仿真。

情況一：當追蹤間隔為12km，第一列機車離牽引變電所4km時，其運行示意圖如圖3所示。

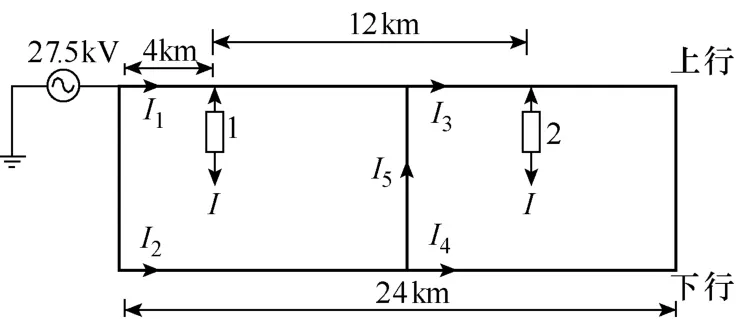
圖3 情況一運行示意圖

通過仿真各電流百分比與并聯點位置的關系，其結果如圖4所示。

由仿真結果可以看出，當并聯點位于距變電所4km時，牽引網的載流需求最高，約為總負荷電流的85%；當并聯點位于距變電所約5km時，此時牽引網的載流需求最低，約為總負荷的57%。

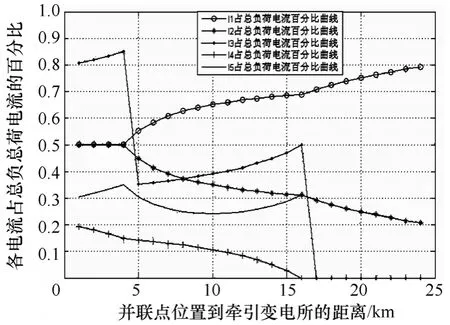
圖4 各電流百分比與并聯點位置的關系曲線

情況二：當追蹤間隔為 8km，第一列機車離牽引變電所4km時，其運行示意圖如圖5所示。

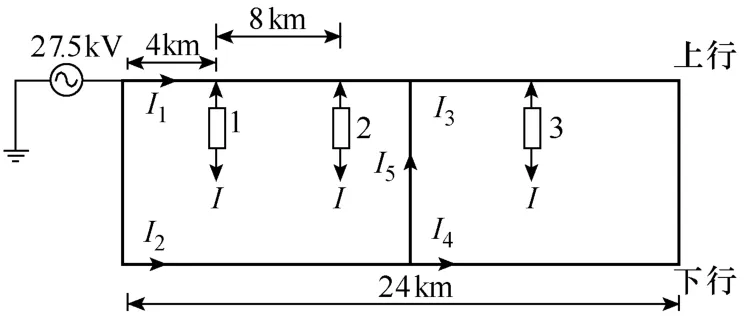
圖5 情況二運行示意圖

通過仿真各電流百分比與并聯點位置的關系，其結果如圖6所示。

由仿真仿真結果可以看出，與情況一結果大致相同，當并聯點位于距變電所4km時，牽引網的載流需求最高，約為總負荷電流的80%；當并聯點位于距變電所約5km時，此時牽引網的載流需求最低，約為總負荷的55%。

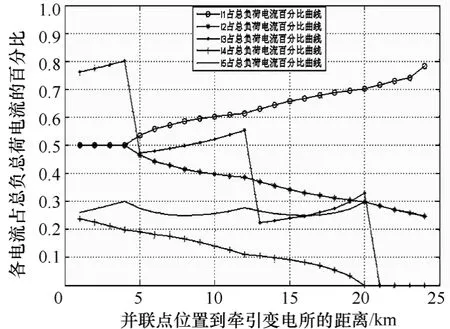
圖6 各電流百分比與并聯點位置的關系曲線

情況三：當追蹤間隔為 6km，第一列機車離牽引變電所4km時，其運行示意圖如圖7所示。

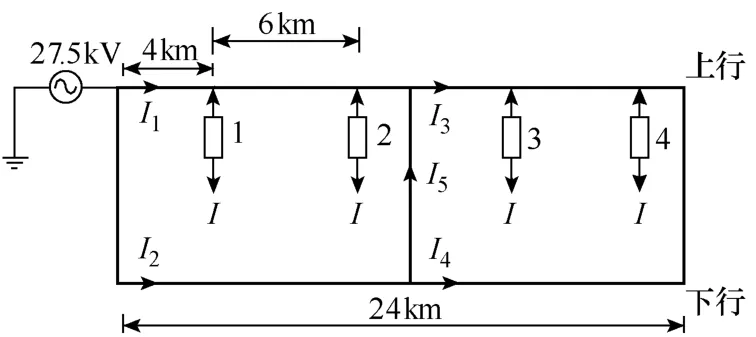
圖7 情況三運行示意圖

同樣通過仿真各電流百分比與并聯點位置的關系，其結果如圖8所示。

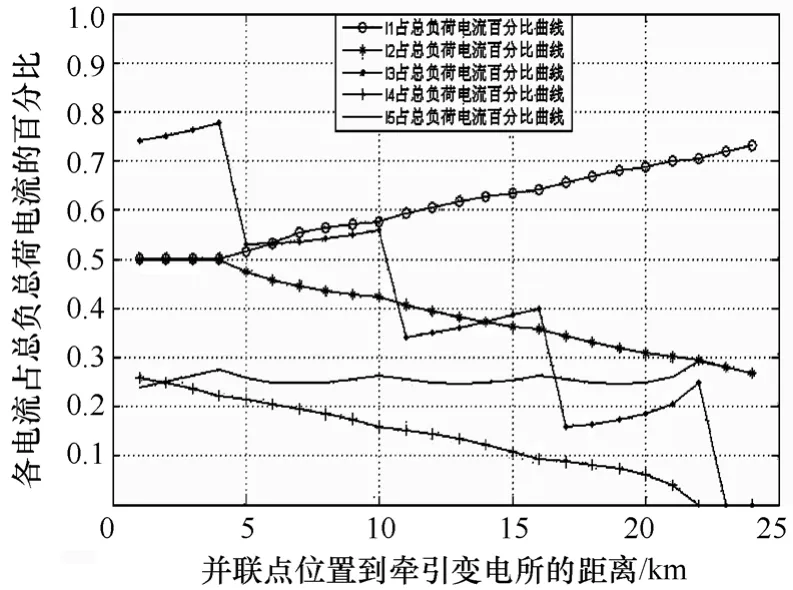
圖8 各電流百分比與并聯點位置的關系曲線

由仿真結果可以看出，當并聯點位于距變電所4km時，與前兩種情況的結果一樣，此時牽引網的載流需求最高，約為總負荷電流的78%；而牽引網最低載流需求與前兩種情況的結果有些差異，出現在并聯點距變電所約6km時，此時牽引網的載流需求約為總負荷的53%。

對上面三種情況下的仿真結果進行比較，相比于上下行分開供電時的 100%總負荷電流的牽引網載流需求，全并聯供電對牽引網的載流需求均有所改善。當并聯點位于供電臂首末兩端時，即與分區所末端并聯一樣，此時牽引網的載流需求約為總電流的75%。隨著并聯點從供電臂首端向末端移動，變電所上行出口電流即I1比例從 50%逐漸增至80%，而變電所下行出口電流即I2比例從50%逐漸減至 20%。隨并聯點位置的不同，流經并聯點的電流即I5比例變化很小，基本維持在25%～30%。

同時對三種情況的仿真結果進行分析可以發現，隨著并聯點位置的移動，當電流I1和電流I3所占總負荷電流比例恰好相等時，牽引網的載流需求最低，選擇在該處進行上下行并聯對牽引網的載流能力提高為最佳。

為了得到一般規律，假設上行負荷的追蹤間隔足夠小時，通過前面仿真可以看出，當I1=I3，即N=4K時，牽引網的載流需求最低，帶入式（8）可以得到如下結果，即并聯點位于供電臂首端處，能最有

效的利用牽引網載流能力，此時載流需求約為總負荷電流的56.25%，相比于分開供電提高了43.75%，比僅在分區所末端并聯提高了23.75%。

以上只分析了供電臂中部并聯一次的情況。不難理解，當供電臂上并聯點足夠多時，總負荷電流將得到充分的均衡，上下行將均勻分擔總負荷電流，此時牽引網的載流需求為總負荷電流的50%。與中部僅并聯一次的最優效果56.25%相比，改善并不明顯。

3 結論

本文從理論上分析了在只有上行有機車負荷時，帶回流線的全并聯直供式系統接觸網電流分布，并給出了中部僅并聯一次時，牽引網的載流需求計算式。通過對三種不同的負荷取流情況進行仿真分析和對比，得到了并聯點位置對牽引網載流能力改善的一般規律，為直供式系統的全并聯方案選擇提供了參考。

[1] 曹建猷.電氣化鐵道供電系統[M].北京:中國鐵道出版社, 1993.

[2] 李群湛,賀建閔.牽引供電系統分析[M].成都:西南交通大學出版社, 2006.

[3] 譚秀炳.交流電氣化鐵道牽引供電系統[M].成都:西南交通大學出版社, 2007.

[4] 鄧云川.關于山區電氣化鐵道牽引供電系統問題的討論[J].電氣化鐵道, 2004, 2萬公里論文集: 188-191.

[5] 繆耀珊.上下行AT牽引網在ATP實行并聯的電能節約[J].電氣化鐵道, 2004(6): 1-3.

[6] 繆耀珊. AT網絡上下行接觸網互為正饋線方式簡介[J].電氣化鐵道, 2005(1): 1-7.

[7] 楚正宇,張長梅.電氣化鐵道直供分區所電氣負荷的分析[J].鐵道工程學報, 2009(6): 94-97.

杜 川 畢業于西南交通大學電氣工程學院，碩士，現于四川省建筑設計院任助理工程師，從事電氣設計工作。