兩千年前的數學奇跡
王綱懷


在銅鏡這個特殊的文物載體上,華夏祖先創造了世界數學史上的奇跡。通過本文,我們可以穿越時空去尋覓:兩千年前為等分圓周的國人,在用尺規作圖時,對數字特別是素數的情懷、喜愛、探索、挑戰。
高斯(1777年至1855年)是德國著名的大數學家、物理學家、天文學家,他是近代數學奠基者之一,在歷史上影響之大可以和阿基米德、牛頓、歐拉并列。他在少年時代就對歐幾里德作圖理論產生了濃厚的興趣,1796年3月30日,終于發現了正十七邊形(正十七邊形之數字17,是素數系列中的一個。要在圓周上用尺規等分除3、5以外的素數,迄今僅由高斯解決了17等分,其他素數在目前皆屬不能解決的數字難題。素數亦稱“質數”。大于1的整數,除了它本身和1以外,不能被其他正整數所整除的,稱為“素數”。)的尺規作圖(初等平面幾何只研究直線形和圓以及由它們組合而成的圖形,并且限定以直尺和圓規為作圖的工具。)法。他曾要求在他去世以后,能將正十七邊形刻在他的墓碑上。雖然這個要求未被滿足,但是在高斯出生地布倫瑞克為他建立的紀念碑底座上有一個正十七邊形,應該說正十七邊形的尺規作圖是數學王子高斯一生成就的奠基石。1855年2月23日,高斯在哥廷根天文臺逝世之后,漢諾威王命令為高斯制作一個紀念章,上面鐫刻有“獻給數學王子”的字樣,從那以后,高斯就以“數學王子”著稱于世。
殊不知,早在1700年至2300年前的中國銅鏡紋飾面上,就已經出現了包括素數17在內的一個圓周等分的數字系列。由此,我們會驚奇地發現,華夏祖先在數學領域上的偉大創造力。
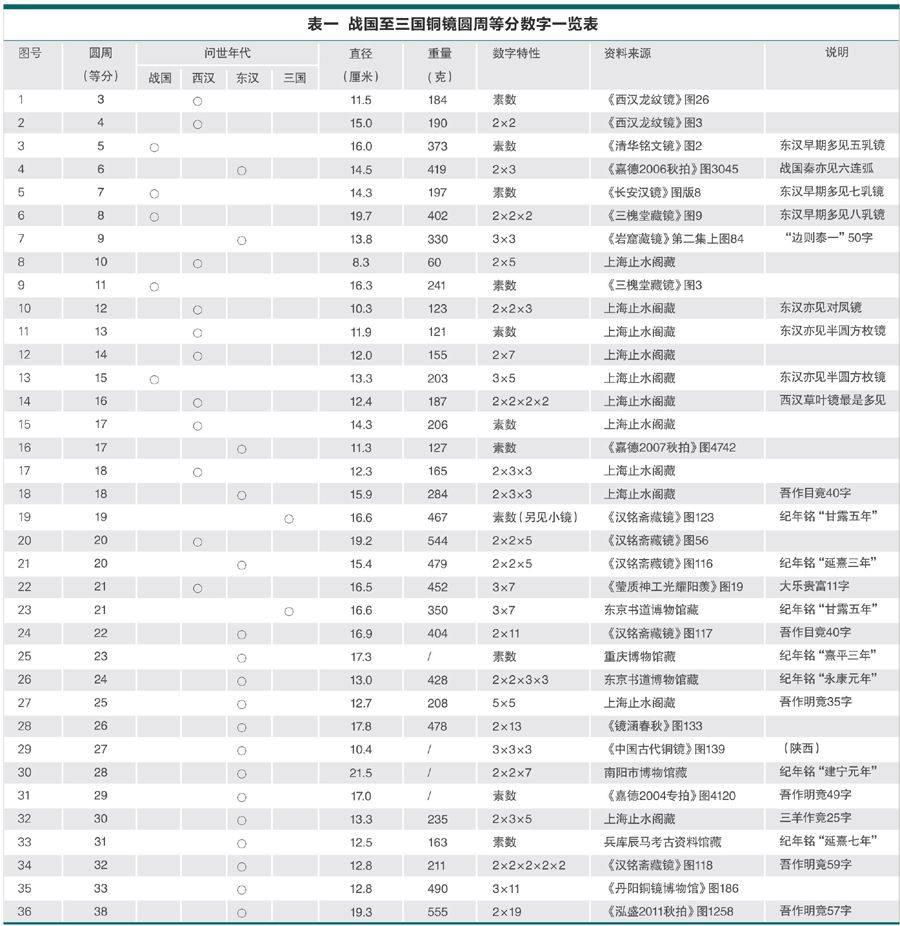
在二十余年的收藏經歷中,筆者時有發現:從戰國至三國的600年間,中國古代銅鏡有著諸多不同的圓周等分數字。經過多年的尋覓查找,癸巳之春,終于找全了從3到33這些數字的連續系列(詳見表一)。
一、據表一可知,數字18(含18)以下者共有18個,按年代與主紋分,有以下多種:
1.戰國——三龍連弧鏡(如:圖13為15連弧)
2.戰國——五山鏡(如:圖3為5等分)
3.戰國——素地連弧鏡(如:圖9為11連弧)
4.戰國秦至西漢——蟠螭紋連弧鏡(如:圖5、6為7、8連弧)
5.西漢早中期——龍紋鏡(如:圖1、2為3、4等分)
6.西漢早中期——連弧鏡(如:圖10、11、12、14、15、17)
7.西漢早中期——草葉鏡、圈帶鏡(連弧多見16,少見18、20)
8.東漢早中期——多乳神獸鏡(乳釘可見5、6、7、8,數字9僅現鈕區)
9.東漢晚期——連弧鏡(如:圖7為9連弧)
二、據表一可知,數字19(含19)以上者共18個,多見于東漢三國,少見于西漢。
1.數字19、20、21重復見于西漢、東漢、三國魏。
2.迄今所知,數字22(含22)以上者,多在東漢變形四葉獸首鏡之中。
3.存世還見大于33的連弧數,如:38(圖36)、48、62等。
三、據表一可知,數字17至21為過渡區,不同的年代皆有出現。
四、新莽時期幾乎皆為四靈博局鏡,似不見有圓周等分的情況。
在表一的36個數字系列中,共有3、5、7、11、13、17、19、23、29、31等10個素數。其間,數字3、5可以用尺規解決,數字17已被德國大數學家高斯破解,還剩7、11、13、19、23、29、31等7個素數,不知漢人如何解決?目前,只能是“知其然而不知其所以然”。我們猜想,即使古人可以用“近似法”這樣既簡易又繁瑣的原始方法,然亦保存了漢人面對不同素數這諸多數學難題的歷史記錄。
戰國晚期至三國魏共約600年。在銅鏡這個特殊的文物載體上,華夏祖先創造了世界數學史上的奇跡。通過本文,我們可以穿越時空去尋覓:2000年前為等分圓周的國人,在用尺規作圖時,對數字(特別是素數)的情懷、喜愛、探索、挑戰。

