無超調不限階數的M型次多容慣性標準傳遞函數

楊 平，陳式躍

（1.上海電力學院電力與自動化工程學院，上海 200090；2.上海量值測控儀器科技有限公司,上海 200090）

0 引 言

在眾多的控制器設計方法中，標準傳遞函數設計法[1]的簡捷性最引人注目。只要已知受控過程模型和確定了期望標準傳遞函數，那么控制器可通過簡單的代數運算來設計。標準傳遞函數設計法的核心是取控制系統的期望傳遞函數為選定的標準傳遞函數。最早提出也是最常用的標準傳遞函數是ITAE標準傳遞函數[2]。比ITAE標準傳遞函數晚8年提出的Butterworth標準傳遞函數[3]可算是僅次于ITAE標準傳遞函數的第2種常用標準傳遞函數。近年來，有關標準傳遞函數本身的研究也出現了一些新進展。在我國，已有不少研究[4-8]對兩種常用標準傳遞函數提出改進。這些改進研究所改變的主要是標準傳遞函數的系數數值。所采用的改進方法有：縮短積分時間域、重新優化計算、選用遺傳算法來優化等。改進的效果主要體現在超調量的減少。與改進研究不同，文獻[9]則提出了一種新標準傳遞函數，稱為多容慣性（multiple capacity process，MCP）標準傳遞函數。這種新的標準傳遞函數具有系統無超調和不限系統階數的特點，并且在工程應用上的通用性更強。不過，文獻[9]的闡述還不夠完善，只給出了1型的多容慣性標準傳遞函數。本文的研究是文獻[9]工作的繼續，將給出任意系統階數的M型次的多容慣性標準傳遞函數，并且更深入地分析了多容慣性標準傳遞函數的動態特性和探討了其工程應用方法。

1 M型次多容慣性標準傳遞函數構建方法

根據基本的控制理論[1]，控制系統的穩態準確性取決于控制系統的型次。若要使某控制系統在階躍輸入下無穩態誤差，則要求該系統的型次至少大于0。若要求系統在斜坡輸入下也無穩態誤差，則要求系統的型次至少大于1。所以，標準傳遞函數應該有不同的系統型次之分。常見的ITAE標準傳遞函數就有1型和2型兩種，而且這兩種函數的同冪項系數是不同的。文獻[9]只給出了1型的多容慣性標準傳遞函數的構建方法。現給出適用于任意系統型次的多容慣性標準傳遞函數的通式：

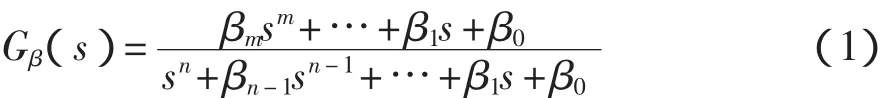
式中：n——多容慣性標準傳遞函數分母多項式的階數，也是系統的階數；

m——多容慣性標準傳遞函數分子多項式的階數；

βi——多容慣性標準傳遞函數多項式的系數。

可以注意到，分母多項式和分子多項式的同冪項系數是相同的，這一點與ITAE標準傳遞函數是相同的。但是，與ITAE標準傳遞函數不同的是，多容慣性標準傳遞函數的多項式系數并不隨系統型次的改變而改變。因此，一旦系統階數和慣性單元時間常數確定，多容慣性標準傳遞函數的多項式系數就確定了，并與所期望的系統型次無關。

式（1）所描述的多容慣性標準傳遞函數系統的型次為

也就是說，多容慣性標準傳遞函數分子多項式的階數m應由所期望的系統型次來確定，即

多容慣性標準傳遞函數的多項式系數βi，可用式（4）計算：

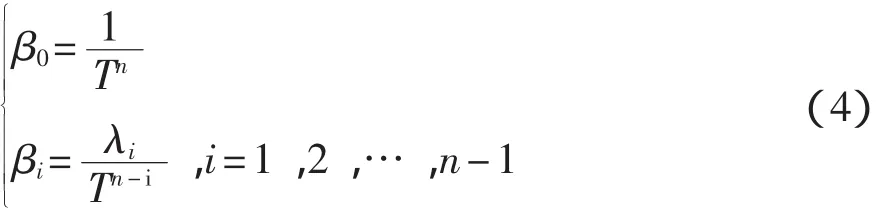
式中：T——慣性單元時間常數；

{λi，i=1，2，…，n-1}——代數二項式系數。

導出多容慣性標準傳遞函數的多項式系數βi的計算式（式（4））的思路是視系統為多個慣性單元串聯而成。設m=0，令

可據代數二項式定理導出

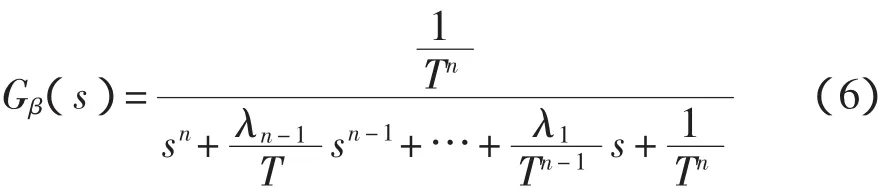
再整理系數并推廣至m≠0，即得式（4）。

慣性單元時間常數T的確定公式如式（7）所示。該式為經驗公式，依據是一階慣性環節的過渡過程時間ts為慣性時間T的3倍（按達到終態值的95%計算），即ts=3T；以及n階慣性環節的過渡過程時間ts可按ts=3nT估計[10]。

根據代數學中的二項式定理，可求得代數二項式系數{λi，i=1，2，…，n-1}如表 1 所示。由系統階數n可確定表1中的行序。表1所示的三角形數陣為著名的楊輝三角形數陣中不含1的內核部分。每行系數值的推算都遵循一個簡單的規則：（1）左右兩端的系數值為階數n；（2）中間的每個系數值為上一行相鄰的兩個系數值之和。例如，n=4行的系數值6可用n=3行的相鄰系數3+3得出，n=5行的系數值10可用n=4行的相鄰系數4+6得出，以此類推。表1只給出15階及以內的各系數值。事實上，依據上述簡單的推算規則，很容易推算出任意高的系統階數數值下的系數值。

表1 多容慣性標準傳遞函數中的系數λi

2 多容慣性標準傳遞函數的系統型次論證

上節所述的多容慣性標準傳遞函數（式（1））的系統型次是否為M可如下論證：

對于系統Gβ（s），設輸入為R（s），輸出為Y（s），則有誤差函數E（s）（見式（8））。代入Y（s）和Gβ（s），則可導出的誤差函數的計算式（式（10）），進而導出穩態誤差的計算式（式（11））。

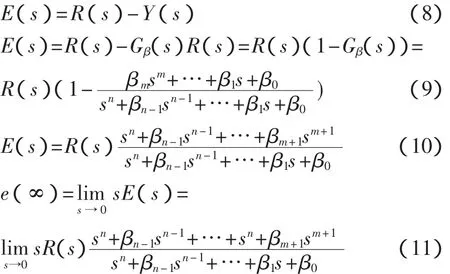
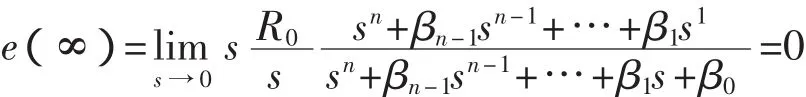
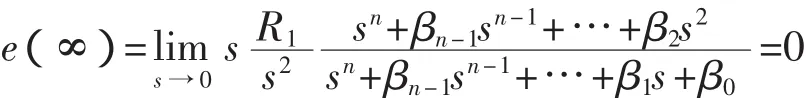
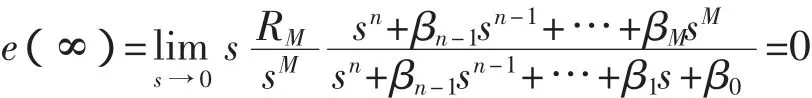
由此可見，由多容慣性標準傳遞函數定義的系統Gβ（s），只要取m=M-1，則Gβ（s）的系統階數為M。

3 多容慣性標準傳遞函數特性分析

3.1 1型系統的階躍響應

設系統型次M=1，設慣性單元時間T=1，分別取系統階數為2，4，6，則有1型多容慣性標準傳遞函數為

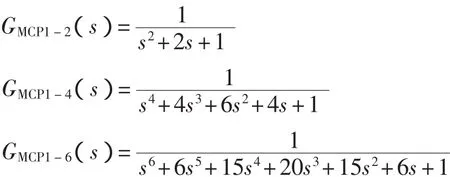
再設慣性單元時間T=0.5，系統階數n=6，有1型多容慣性標準傳遞函數為

為了比較，取自然振蕩頻率ωn=1，據文獻[1]中表4-5，算得1型6階的ITAE標準傳遞函數為

利用Matlab/Simulink動態系統仿真平臺，可得上述5種系統的單位階躍響應和誤差響應如圖1和圖2所示。按達到終態值的95%為線，從誤差響應圖上可測得5種系統的調整時間值如表2所示。

從圖1和圖2以及表2可看出：（1）在慣性單元時間T=1條件下，多容慣性標準傳遞函數所述系統的調整時間ts與系統階數n成正比關系，基本符合式（7）所述關系；（2）多容慣性標準傳遞函數所述系統的響應沒有超調；（3）在系統階數n=6條件下，ITAE標準傳遞函數所述系統的調整時間ts可能比多容慣性標準傳遞函數所述系統長（T=1時），也可能比多容慣性標準傳遞函數所述系統短（T=0.5時）。換言之，通過調整T值的大小可獲得系統調整時間的期望值。

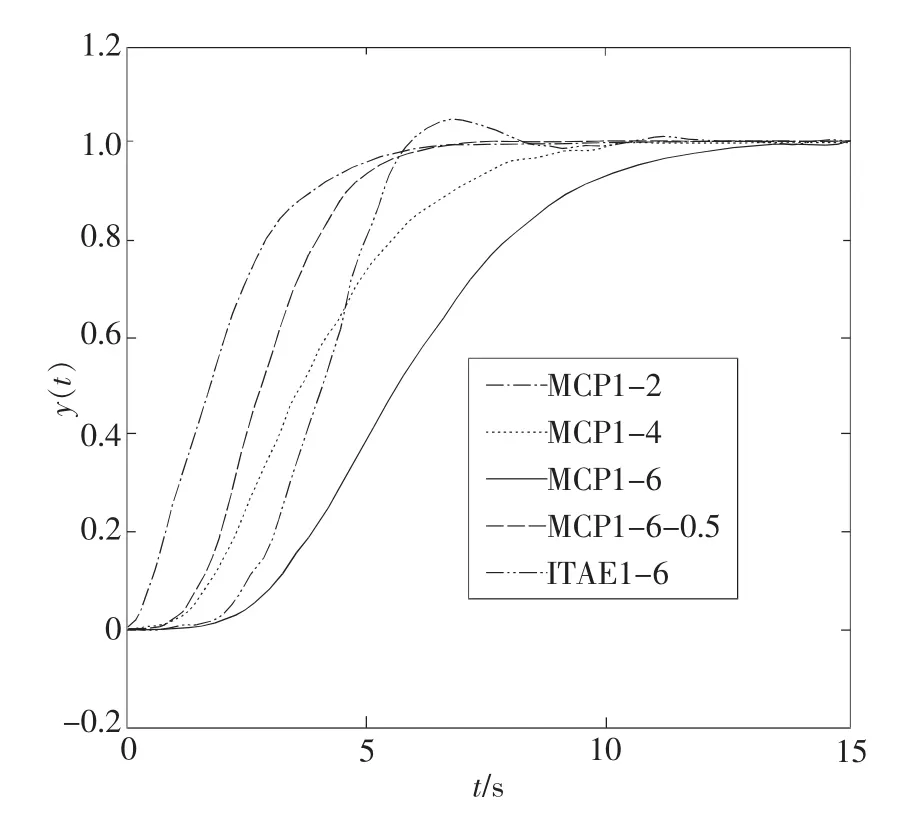
圖1 1型標準函數系統的階躍響應

圖2 1型標準函數系統的階躍響應誤差

表2 t s的計算和實測

表2不但給出了5種系統的調整時間測得值，還給出了對應的計算值。比較這些數值，可知實測值均小于計算值，而且是階數越高，差值越大。不過從留有余地的保守性設計角度出發，這種誤差還是可以接受的。

3.2 2型系統的斜坡響應

設系統型次M=2，設慣性單元時間T=1，分別取系統階數為2，4，6，則有2型多容慣性標準傳遞函數為

再設慣性單元時間T=0.5，系統階數n=6，有2型多容慣性標準傳遞函數為

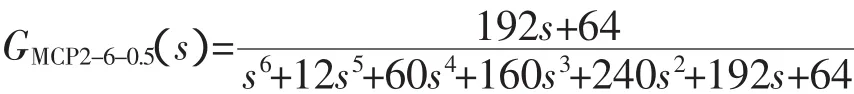
為了比較，取自然振蕩頻率ωn=1。據文獻[2]（Graham&Lathrop）中的ITAE標準傳遞函數數據，算得6階的2型ITAE標準傳遞函數為

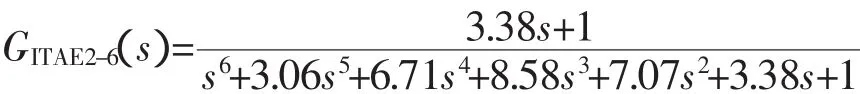
利用Matlab/Simulink動態系統仿真平臺，可得上述5種系統的單位斜坡響應和誤差響應如圖3和圖4所示。

從圖3和圖4同樣可看出：多容慣性標準傳遞函數所述系統的斜坡響應也像階躍響應一樣沒有超調；其過渡過程時間與階躍響應中定義的調整時間相當；在n=6條件下，ITAE標準傳遞函數所述系統的過渡過程時間比多容慣性標準傳遞函數所述系統時的要長，比T=0.5時要短。

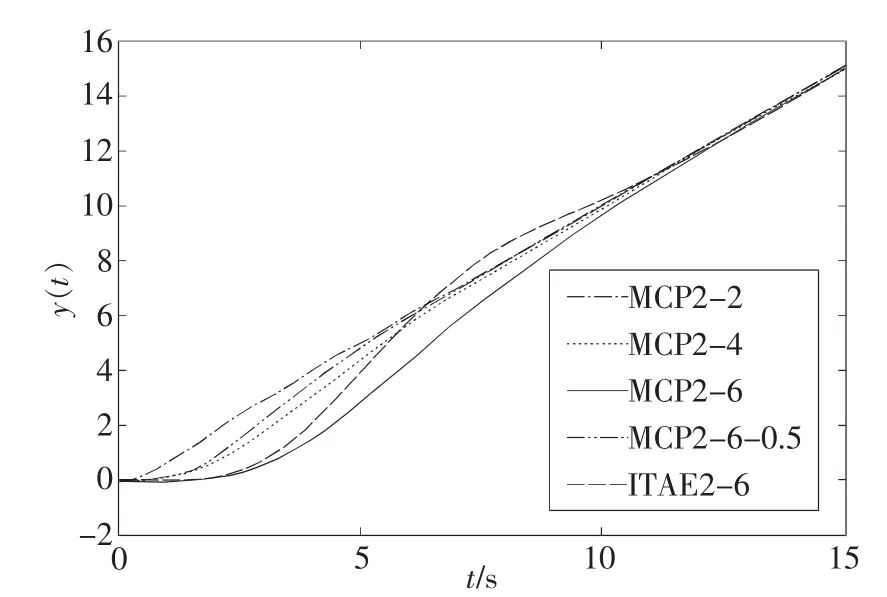
圖3 2型標準函數系統的斜坡響應

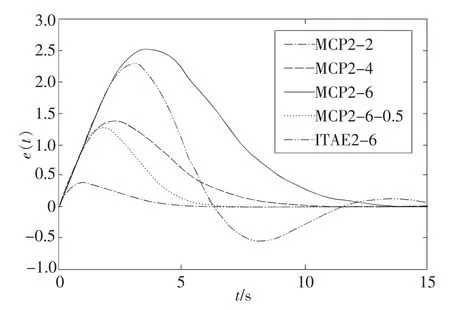
圖4 2型標準函數系統的斜坡響應誤差

4 多容慣性標準傳遞函數的應用探討

在文獻[11]中，專門討論了應用標準傳遞函數設計控制器的理論方法，考慮了串聯校正型、反饋校正型和狀態反饋型控制器的設計問題。并且針對1型標準傳遞函數無零點的特點，分別導出了串聯校正型、反饋校正型和狀態反饋型控制器的設計約束條件。還針對有零點的被控過程提出了應用直接設計法和補償法兩種解決方案。

在文獻[12]中，專門討論了應用多容慣性標準傳遞函數設計狀態反饋型控制器的問題，也是應用無零點的1型標準傳遞函數。由于狀態反饋型控制器不會增加系統零點，所以更易滿足無零點約束條件。此外，在文獻[12]中所述的被控過程本身的階數高達9階，若采用ITAE標準傳遞函數，則找不到數據，而用多容慣性標準傳遞函數，其不限階數的優勢盡現。

M型次的多容慣性標準傳遞函數的提出，打破了1型多容慣性標準傳遞函數的應用局限，為應用標準傳遞函數設計控制器提供了更大的設計空間。例如，針對2型標準傳遞函數，控制器的設計約束條件將從無零點變為可有一個零點，所設計系統的型次也從1型提高至2型。

以下以管式檢定爐的溫度控制為例，應用1型多容慣性標準傳遞函數設計一個串聯校正型控制器。

考慮圖5所示的典型的串聯校正型控制系統。其中，Gc（s）是控制器傳遞函數，Go（s）是被控過程傳遞函數，R是系統的設定值輸入，Y是系統輸出。系統總的傳遞函數W（s）如式（12）所示。

圖5 串聯校正型控制系統

應用直接設計公式式（13）可得控制器Gc（s）。

假設已知被控過程管式檢定爐的數學模型[13]如式（14）所示，這是一個有零點的被控過程。

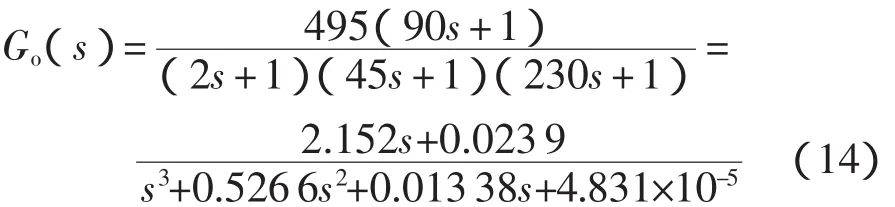
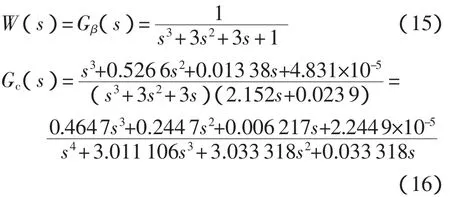
利用Matlab中的simulink平臺，可搭建相應的仿真試驗系統。將利用直接設計公式設計的多容慣性標準傳遞函數控制器Gc（s）置入試驗系統，并與一個常規的PID控制系統（設PID參數為Kp=0.6，Ti=2.04，Td=4）同時進行階躍響應試驗，可獲得如圖6所示的階躍響應曲線。其中，短劃線是期望的標準傳遞函數響應，實線曲線是PID控制響應，點劃線是所設計的控制系統響應。顯然，所設計的控制系統響應曲線與標準傳遞函數響應曲線完全重合，其無超調量和調整時間短的特性遠比PID控制響應優越。

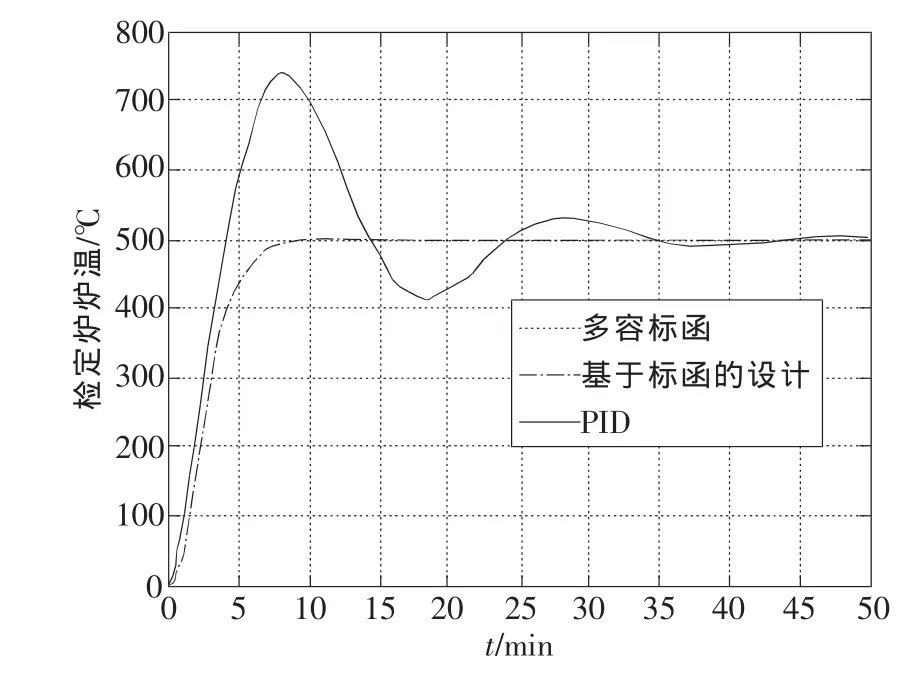
圖6 檢定爐溫度控制響應

5 結束語

與ITAE標準傳遞函數相比，以上提出的通用的多容慣性標準傳遞函數具有無超調和不限系統階數的鮮明特點。通用多容慣性標準傳遞函數的系統型次為M已得到論證。而且，構建任意數值的系統型次的多容慣性標準傳遞函數非常容易。多容慣性標準傳遞函數所表達的系統的階躍響應和斜坡響應特性分析，充分展示了無超調特性和調整時間與3nT成正比的關系。應用通用的多容慣性標準傳遞函數進行控制器的設計方法討論表明，利用控制器直接設計公式和狀態反饋極點配置是兩種常用的簡單和有效的應用方法。

[1]楊平，翁思義，郭平.自動控制原理－理論篇[M].北京：中國電力出版社，2009：147-155.

[2]Graham D，Lathrop R C.The Synthesis of optimum transient response criteria and standard forms[J].A IEE Trans，1953（72）：273.

[3]Schultz W C，Rideout C V.Control system performance measures：past，present and future[J].IRE Trans Automatic Control，1961，26（22）：.

[4]楊益群，項國波.新的ITAE最佳傳遞函數標準型[J].信息與控制，1999，26（4）：259-265.

[5]李鎮銘.環路法及最佳狀態反饋系統設計[M].北京：國防工業出版社，1988：120-134.

[6]張志涌，劉瑞楨.對經典ITAE傳遞函數標準型的研究[J].福州大學學報，1977，25（3）：120-121.

[7]李鐘慎.位移無靜差最優傳遞函數的研究[J].自動化博覽，2007（2）：82-84.

[8]洪健，李鐘慎.改進的Butterworth最佳傳遞函數標準型[J].計算技術與自動化，2005，24（2）：13-15.

[9]楊平，余潔，孫宇貞.多容慣性標準傳遞函數的建立與比較[J].上海電力學院學報，2011，27（5）：512-514，518.

[10]李旭.過熱汽溫的動態特性與控制[J].動力工程，2007，27（2）：23-28.

[11]楊平.控制器的標準傳遞函數設計方法[J].化工自動化及儀表，2010，37（11）：9-13.

[12]楊平，張玲芳，于會群.鍋爐汽溫狀態反饋控制器的標準傳遞函數設計方法[J].熱力發電，2011，40（1）：35-39.

[13]楊平.管式電阻爐的動態特性[J].上海電力學院學報，1986（2）：25-30.