貢湖湖區(qū)風(fēng)浪要素計(jì)算方法探討

唐馨婷 劉曙光 高 怡

1.同濟(jì)大學(xué)土木工程學(xué)院水利工程系，上海 200092；

2.水利部太湖流域管理局水文水資源監(jiān)測局，江蘇 無錫 214024

湖泊，是陸地表面洼地積水形成的水域?qū)拸V、流動(dòng)緩慢的水體形式，也是人類開展生產(chǎn)、生活活動(dòng)的主要區(qū)域之一。水作為湖泊中傳遞物質(zhì)和能量的載體，通過水體運(yùn)動(dòng)的基本形式，實(shí)現(xiàn)了湖泊中的物質(zhì)的輸移以及能量的轉(zhuǎn)換[1]。貢湖是太湖東北部的一個(gè)湖灣，水面面積為146km2，湖區(qū)內(nèi)重要水源地有無錫南泉水廠、錫東水廠和蘇州金墅港水源地。目前貢湖灣建有貢湖水質(zhì)自動(dòng)站和風(fēng)浪站，自2006年以來，取得了大量的水質(zhì)和風(fēng)浪監(jiān)測數(shù)據(jù)。

隨著社會(huì)經(jīng)濟(jì)的全面發(fā)展，人類對水資源的需求量越來越大、對水質(zhì)的要求越來越高，然而，隨著我國國民經(jīng)濟(jì)的快速發(fā)展，太湖水質(zhì)富營養(yǎng)化嚴(yán)重、水華頻發(fā)，水污染問題越來越嚴(yán)重，貢湖水源地的供水安全受到了嚴(yán)重威脅。

近年來對以太湖為代表的大型淺水湖泊的研究表明，強(qiáng)烈的水動(dòng)力作用是導(dǎo)致水-沉積物界面不穩(wěn)定、沉積物再懸浮和營養(yǎng)鹽內(nèi)源釋放、生長層內(nèi)部結(jié)構(gòu)和生物數(shù)量變化、光學(xué)吸收、衰減等物理、化學(xué)、生物過程的重要驅(qū)動(dòng)力[2-4]。而在影響底泥內(nèi)源釋放的水動(dòng)力作用中，風(fēng)浪是最主要的作用力之一。因此，開展湖泊風(fēng)浪的研究，對防洪減災(zāi)工作、發(fā)展湖區(qū)的經(jīng)濟(jì)建設(shè)具有重要的科學(xué)意義[1]，對貢湖湖區(qū)風(fēng)浪要素計(jì)算方法的研究刻不容緩。

1 存在的問題

目前，計(jì)算風(fēng)浪要素有許多種方法，有些是經(jīng)驗(yàn)的，有些是半經(jīng)驗(yàn)半理論的，也有一些是純理論的[5]。在太湖風(fēng)浪特征研究方面，喬樹梁等人[6]曾于1992年和1993年的8～11月間，在無錫馬山附近的湖面上，進(jìn)行了風(fēng)浪觀測，并且根據(jù)實(shí)測資料，系統(tǒng)地分析了湖泊風(fēng)浪的特性，進(jìn)而提出了湖泊風(fēng)浪要素的計(jì)算方法：

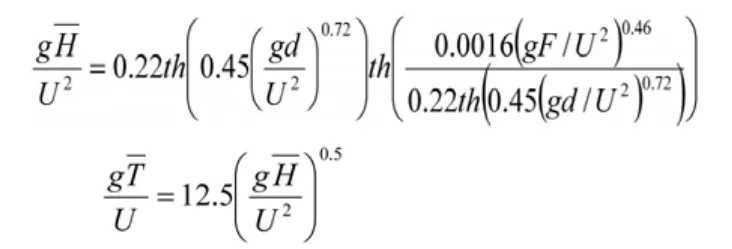
該公式在認(rèn)識(shí)太湖風(fēng)浪特征及計(jì)算太湖風(fēng)浪要素方面發(fā)揮了重要作用[2]。然而，通過湖泊風(fēng)浪要素計(jì)算公式計(jì)算出來的結(jié)果，與貢湖湖區(qū)風(fēng)浪觀測站實(shí)測資料對比發(fā)現(xiàn)（見表1）：該經(jīng)驗(yàn)公式計(jì)算值與實(shí)測值相差較大。當(dāng)風(fēng)區(qū)長度達(dá)到50km時(shí)，最高誤差可達(dá)到60%以上。因此可以推測，風(fēng)浪資料具有較明顯的地區(qū)性，風(fēng)浪的發(fā)展，除了受到水深、風(fēng)區(qū)長度以及風(fēng)速的直接影響外，還受到地形以及水生植物種類的影響[5,7]。并且，由于當(dāng)時(shí)觀測手段的不同、設(shè)備精確度的限制、觀測數(shù)據(jù)的整理方法以及觀測點(diǎn)距離湖岸較近且為單點(diǎn)觀測等因素的影響[5,7]，其結(jié)果是否適用貢湖湖區(qū)有待進(jìn)一步的討論和分析。

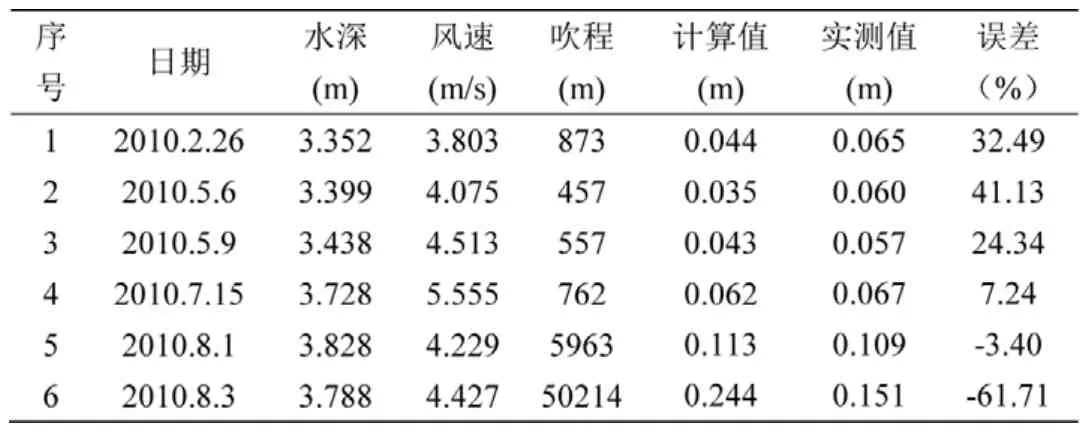
表1 風(fēng)浪要素實(shí)測與計(jì)算波高統(tǒng)計(jì)

2 研究現(xiàn)狀

目前適合淺水的風(fēng)浪要素計(jì)算方法主要有：美國的SMB法、小風(fēng)區(qū)風(fēng)浪公式、青島海洋大學(xué)法、莆田實(shí)驗(yàn)站法、淺水湖泊風(fēng)浪公式和日本的井島公式等。

其中，莆田實(shí)驗(yàn)站法是由河海大學(xué)洪廣文等根據(jù)福建莆田實(shí)驗(yàn)站觀測資料，考慮了風(fēng)速、風(fēng)區(qū)長度和水深的影響，提出的一個(gè)適用于深、淺水的風(fēng)浪要素計(jì)算方法，該方法已為我國水利部《碾壓式土石壩規(guī)范》所采用[1]，其公式為：

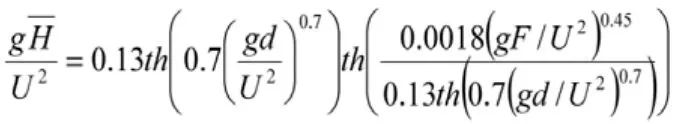
截止目前研究表明，不同湖泊的風(fēng)浪可以以莆田實(shí)驗(yàn)站公式為基礎(chǔ)進(jìn)行風(fēng)浪要素?cái)M合計(jì)算。趙利平等[1]以洞庭湖風(fēng)浪實(shí)測資料為依據(jù)，主要對目前國內(nèi)外常用的風(fēng)浪要素計(jì)算方法進(jìn)行了比較，并且在莆田實(shí)驗(yàn)站公式的基礎(chǔ)上反復(fù)調(diào)試，得出適合于洞庭湖區(qū)的風(fēng)浪要素計(jì)算公式；曹勇等[8]對淀山湖對淀山湖風(fēng)浪開展現(xiàn)場觀測，以莆田實(shí)驗(yàn)站公式為基礎(chǔ)，對測定結(jié)果進(jìn)行擬合得出淀山湖趙田湖水域風(fēng)浪平均波高的經(jīng)驗(yàn)計(jì)算公式。

3 研究方法

3.1 風(fēng)浪要素觀測

貢湖湖區(qū)上的風(fēng)浪觀測站每秒鐘產(chǎn)生4個(gè)風(fēng)浪監(jiān)測數(shù)據(jù)，包括風(fēng)速、風(fēng)向、波高、水深等風(fēng)況及風(fēng)浪要素資料。具體的站點(diǎn)坐標(biāo)位置如下（見圖1）：

貢湖站（120 °23 ’45 .4”，31°26’38.0”）

大浦口站（119 °55 ’52 .3”，31°15’57.8”）

平臺(tái)山站（120 °06 ’20 .2”，31°13’54.5”）

3.2 相關(guān)影響因子的確定

風(fēng)浪一旦生成，周圍的不同影響因子會(huì)對它產(chǎn)生不同的影響，其中主要的影響因子有：風(fēng)況（包括：風(fēng)速、風(fēng)向、風(fēng)時(shí)和風(fēng)區(qū)長度）、水深和海流等[5]。

根據(jù)《堤壩工程設(shè)計(jì)規(guī)范》（GB50286-98），當(dāng)研究區(qū)域的風(fēng)區(qū)長度≤100km時(shí)，可以不考慮風(fēng)時(shí)的影響[8]。貢湖風(fēng)區(qū)長度小于100km，因此風(fēng)時(shí)不作為計(jì)算該湖區(qū)風(fēng)浪要素的主要影響因子。

因此，根據(jù)相關(guān)規(guī)定及前人的研究基礎(chǔ)，本文擬定風(fēng)速、水深、風(fēng)區(qū)長度為貢湖湖區(qū)風(fēng)浪主要影響因素。

4 擬合結(jié)果及驗(yàn)證

4.1 擬合

首先設(shè)定參數(shù)a1、a2、a3、a4、a5，風(fēng)浪計(jì)算公式可以用如下形式表示：

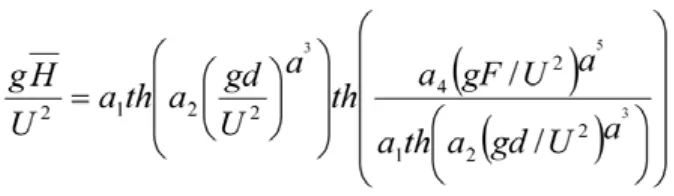
利用數(shù)值計(jì)算軟件，通過最小二乘法，以貢湖湖區(qū)風(fēng)浪站實(shí)測資料為基礎(chǔ)，對參數(shù)a1、a2、a3、a4、a5進(jìn)行非線性擬合，計(jì)算得出參數(shù)的最佳估計(jì)值（表1）。因此，可以得出貢湖湖區(qū)風(fēng)浪要素的計(jì)算公式為：

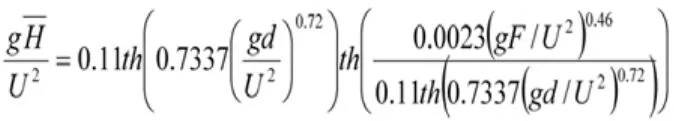
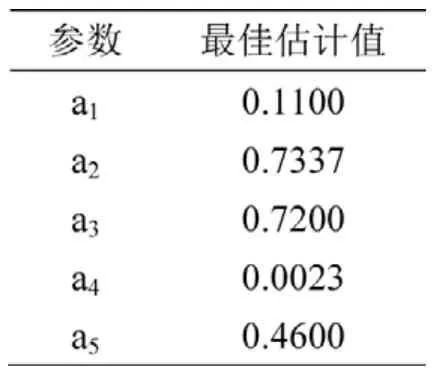
表1 參數(shù)估計(jì)表

由圖2可以看出，通過對該公式的計(jì)算值和實(shí)測波高值得對比，擬合值與實(shí)測值的誤差基本上在±30%以內(nèi)，擬合程度較好。

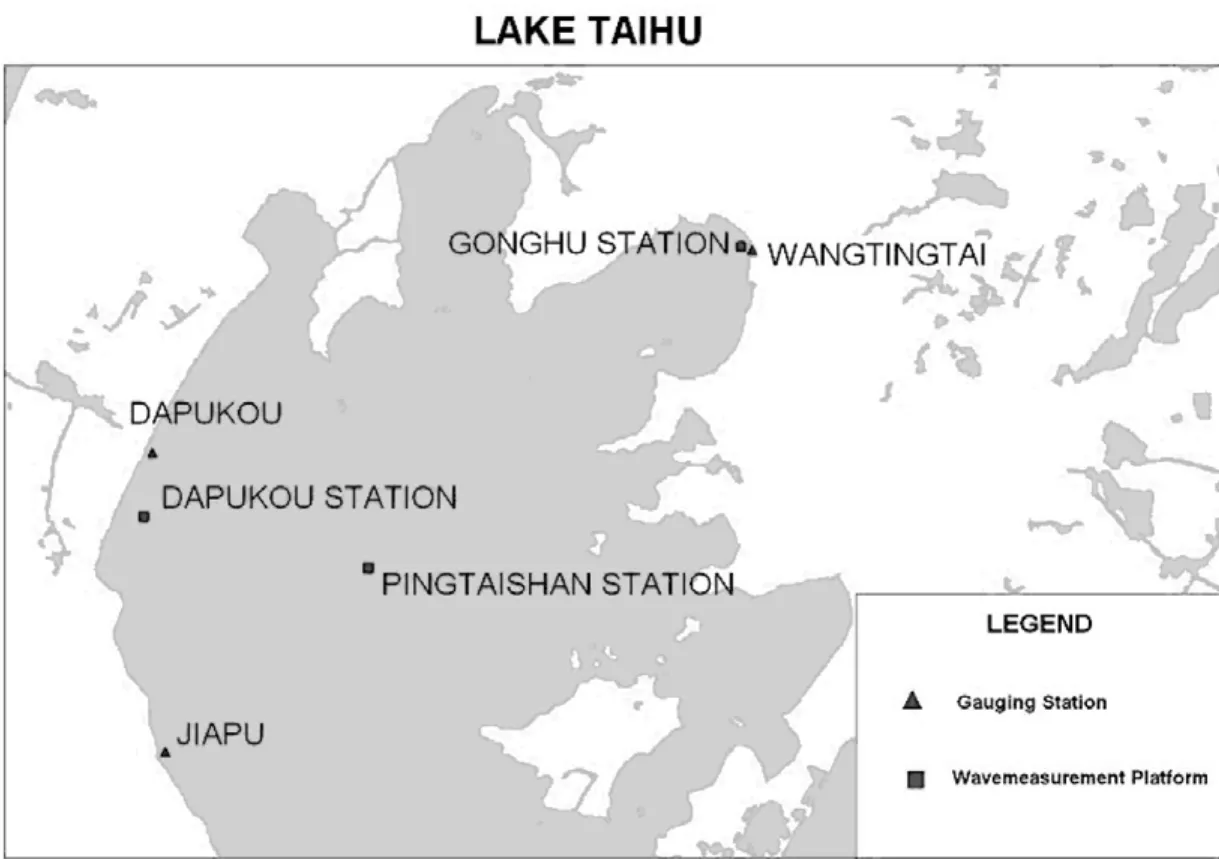
圖1 太湖風(fēng)浪觀測站分布

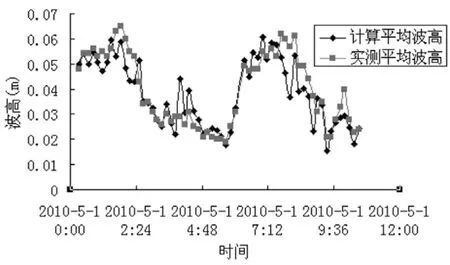
圖2 波高擬合值與實(shí)測值對比

圖3 擬合校驗(yàn)結(jié)

4.2 驗(yàn)證

為驗(yàn)證擬合公式的準(zhǔn)確度，對2010年10月14日風(fēng)浪站觀測數(shù)據(jù)進(jìn)行采集，并利用上述擬合公式進(jìn)行計(jì)算，得到觀測時(shí)段內(nèi)的太湖風(fēng)浪要素計(jì)算值，并用實(shí)測值對計(jì)算結(jié)果進(jìn)行驗(yàn)證。根據(jù)統(tǒng)計(jì)（圖3），實(shí)測值與計(jì)算值的誤差基本在±30%以內(nèi)，擬合效果較好。因此證明所得出的擬合關(guān)系式適合貢湖湖區(qū)風(fēng)浪實(shí)際情況，可用于計(jì)算貢湖風(fēng)浪的平均波高。

5 結(jié)語

本研究在考慮了風(fēng)速、水深以及風(fēng)區(qū)長度這三個(gè)風(fēng)浪成長主要影響因子的前提下，通過對貢湖風(fēng)浪觀測平臺(tái)的觀測數(shù)據(jù)進(jìn)行擬合及率定，得到了適合于貢湖湖區(qū)的風(fēng)浪要素計(jì)算經(jīng)驗(yàn)公式為：

分析結(jié)果表明，不同湖區(qū)由于其水下地形以及水環(huán)境條件的差異，應(yīng)根據(jù)研究區(qū)域具體情況選用適合該區(qū)域的風(fēng)浪計(jì)算公式。本文以貢湖風(fēng)浪平臺(tái)實(shí)測資料為基礎(chǔ)，在莆田試驗(yàn)站風(fēng)浪要素計(jì)算公式的基礎(chǔ)上，對該公式進(jìn)行擬合，并通過對修正后的計(jì)算公式所得到的計(jì)算值與實(shí)測值進(jìn)行比較，發(fā)現(xiàn)計(jì)算值與風(fēng)浪要素實(shí)測值吻合度較好。該公式可完善現(xiàn)有的太湖水動(dòng)力學(xué)模型，掌握在不同風(fēng)浪作用下的沉積物再懸浮特征與水體營養(yǎng)鹽濃度變化情況，從而為太湖底泥生態(tài)疏浚和突發(fā)性水污染事件預(yù)警提供依據(jù)。

[1]趙利平，沈浩，沈小雄.洞庭湖區(qū)風(fēng)浪要素計(jì)算的探討[J].長沙交通學(xué)院學(xué)報(bào)，2004(20)

[2]李一平，逄勇，劉興平等.太湖波浪數(shù)值模擬[J].湖泊科學(xué)，2008，20(1)：117-122

[3]秦伯強(qiáng)，朱廣偉，張路等.大型淺水湖泊沉積物內(nèi)源營養(yǎng)鹽釋放模式及其估算方法——以太湖為例[J].中國科學(xué)，2005，35(z2)：33-44

[4]FAN C X，ZHANG L，QU W C. Lake sedements resuspension and casused phosphate release-A simulation study[J]. Journal of Environmental Science，2001，13(4)：406-410

[5]滕學(xué)春，吳秀杰，董吉田.淺水風(fēng)浪要素計(jì)算方法[J].黃渤海海洋，1985，3(3)

[6]喬樹梁，杜金曼，陳國平等.風(fēng)浪特征及風(fēng)浪要素的計(jì)算[J].水利水運(yùn)科學(xué)研究，1996，3：189-198

[7]胡維平，胡春華，張發(fā)兵等.太湖北部風(fēng)浪波高計(jì)算模式觀測研究[J].湖泊科學(xué)，2005，17(1)：41-46

[8]曹勇，孫從軍，高陽俊等.淀山湖水域風(fēng)浪要素計(jì)算研究[J].長江流域資源與環(huán)境，2011，20(1)：39-43