預定相遇態勢的魚雷二次轉角射擊通用模型與算法
李長文, 李本昌, 初 磊
?
預定相遇態勢的魚雷二次轉角射擊通用模型與算法
李長文, 李本昌, 初 磊
(海軍潛艇學院 科研部, 山東 青島, 266042)
為了解決預定相遇態勢二次轉角射擊參數的計算問題, 考慮魚雷可能的變速及特殊彈道過程, 建立了可滿足不同射擊方式需求的通用數學模型, 給出了牛頓迭代算法的相關公式。用數值實驗的方法對模型及算法的正確性進行了驗證, 結論表明模型及算法可滿足直航、聲自導、尾流自導、齊射、目標選擇等射擊參數計算的需求。
魚雷; 預定相遇態勢; 二次轉角; 射擊參數
0 引言
對于非線導雷射擊, 魚雷射擊的目的實際上應為滿足特定的命中態勢, 所謂命中態勢即假設無誤差條件下與魚雷固連的遮蓋中心及與目標固連的瞄準點相遇時刻的態勢。當對命中角不作要求時, 可以用一次轉角射擊實現, 若對命中角有要求, 一般必須采用二次轉角射擊實現。
對魚雷命中角有要求的情形包括: 尾流自導的進入角、有利于聲自導探測的命中角、攻擊舷別與目標舷別不同的情形等。當考慮預設命中角時, 同時還必需考慮魚雷完成二次轉角及自導開機等特殊彈道至遮蓋中心與瞄準點(假設無誤差無自導條件下)相遇的直航距離, 以滿足搜索彈道的目標選取及遮蓋可能的誤差等需要, 所謂預定相遇態勢就是指規定命中角以及這個距離。
關于預定相遇態勢的二次轉角射擊的意義和作用, 參見文獻[1]。本文將就這一問題進行抽象, 試圖建立一個通用模型, 并研究求解的算法。
1 二次轉角射擊輸入輸出參數及描述模型
1.1 目標及瞄準點
艦艇為一個有一定長度L的運動目標, 規定其參考坐標系原點O為艦艉,x-軸正方向為艉艏線方向,y軸正方向為艦艇在水平面上的正右方向,z軸正方向為豎直向下方向。瞄準點是與這個運動的參考系固連的一個點, 對于只考慮水平面上運動的情形,點位于xOy面上, 其對應的復數為

式中:為瞄準點到艦艉的距離;X為瞄準點在水平面上關于目標的舷角;X= 0或p對應的瞄準點位于目標正前方或正后方。對于聲自導魚雷射擊, 通常取= 0,X的取值無影響, 對于直航魚雷通常取= 0.5L,X= 0, 對于尾流自導魚雷射擊, 通常取= 0.5(Vt–L),X=p,t為尾流持續時間。
1.2 遮蓋中心
魚雷為一個有一定長度的運動目標, 規定其參考坐標系原點O為前端點,x-軸正方向為艉艏線方向,y軸正方向為魚雷在水平面上的正右方向,z軸正方向為豎直向下方向。遮蓋中心是與這個運動的參考系固連的一個點, 其作用為, 進行射擊參數計算時, 在假設無誤差無自導條件下, 遮蓋中心將與瞄準點相遇。對于只考慮水平面上運動的情形,點位于xOy面上, 對應的復數為

式中:R為遮蓋中心到魚雷的距離;為遮蓋中心相對魚雷的舷角。對于聲自導魚雷, 若取半徑為半頂角為的聲自導扇面的形心為遮蓋中心, 則R= 2sin/ ( 3),= 0。對于直航或尾流自導魚雷, 遮蓋中心即魚雷, 相當于R= 0。
1.3 射擊態勢
所謂射擊態勢是指潛艇采用目標運動要素時刻(稱為0時刻)潛艇位置點與目標位置點構成的相對態勢。潛艇位置點為對目標的觀測站, 這個點到魚雷出管位置點的距離以0表示, 假設潛艇發射魚雷前作等速直航運動, 其設定(速率, 航向)以(,)表示, 真實速率(速率, 航向)以(0,0)表示。
目標位置點為目標艦艉, 0時刻的目標運動要素以(方位, 距離, 速率, 航向)表示。目標運動要素有真值與觀測值之分, 真值是客觀存在的, 基于真值進行仿真研究, 所得結論是客觀的, 即可用重復試驗的方法進行驗證的, 因此可用于魚雷效能評估。目標運動要素觀測值一般是由純方位等方法解算的, 一定條件下可以看成真值、系統誤差、隨機誤差通過特定系統的輸出, 目標運動要素觀測值是魚雷射擊現場決策的起點, 主要用于計算射擊參數, 分別以(0,0,0,0)和(,,,)表示目標(方位, 距離, 速率, 航向)真值和觀測值。
目標距離是指目標方位線上的距離, 目標方位有實際方位與可觀測方位之分, 可觀測方位是指由觀測設備給出的目標聲信號的到達方位, 由于聲速有限的延遲作用, 可觀測方位不等于實際方位, 其差異程度與目標聲源到觀測站的距離密切相關, 若采用目標運動要素時刻的方位取當前時刻的可觀測方位, 則應考慮聲速的作用, 假設聲音傳播相當于速率V的勻速直線運動, 則無誤差條件下0時刻目標實際位置點為O=e+(/V)e。由于目標運動要素一般是通過對目標的觀測解算的, 解算過程中可以假設作為運動要素的目標方位和距離為實際方位和距離, 因此, 可以不再考慮聲速的作用, 無誤差條件下0時刻的目標實際位置點為O=e, 下面將運用這一假設。
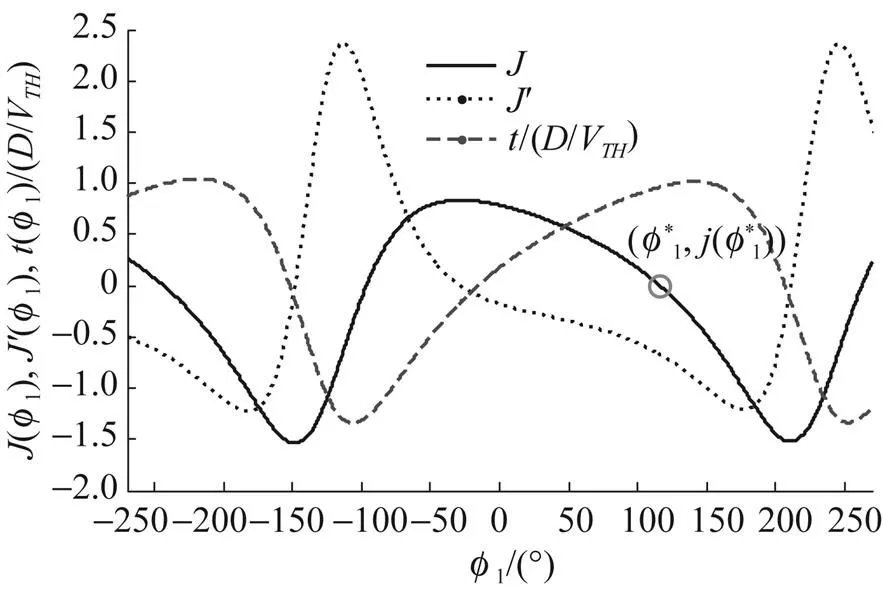
用于射擊參數計算的決定發射魚雷時刻潛艇與目標的相對態勢還可以用潛艇相對目標的距離觀測值、速率觀測值、舷角觀測值、潛艇速率設定值以及目標相對潛艇舷角設定值X表示, 這時, 給定目標方位對應的目標航向、潛艇航向的觀測值可表示為= rb(––p),= rb(–X)。rb()為自定義函數, 其作用為將角變為[–p,p) 上與終邊相同的角, 計算公式為: 若 mod(, 2p) 為達成發射魚雷的目的, 需要為魚雷設計相應的彈道, 這就要考慮魚雷的彈道邏輯。為便于表達, 此處不考慮魚雷初始彈道可能的復雜變速、變深、以及特殊彈道在時空上的作用, 下面的假設只是用于說明一些方法的學術研究, 不能用于實際目的。 假設魚雷出管后在水平面上投影點的運動為直線或圓周運動, 自0時刻至魚雷出管的時間以0表示, 魚雷出管后經時間01完成一些變速變深等運動, 速率穩定于V1, 在水平面上航行的距離為, 之后以角速率1執行水平面上的一次轉角1的勻速圓周運動, 轉角運動結束后直航, 至初次變速時刻進行V1到V的變速, 初次變速時刻以魚雷出管后的時間表達,的設定值應與初次變速前的魚雷彈道邏輯相容, 假設變速運動在水平面上為直線運動, 變速時間為(V1,V)、水平面上航行的距離為(V1,V), 變速運動完成后魚雷以速率V進行水平面上的等速直航。至二次轉角時刻以角速率2執行二次轉角2的勻速圓周運動, 二次轉角完成后執行一些規定的特殊彈道, 完成這個特殊彈道所用時間以表示,= 0表示無特殊彈道。對于> 0的情形, 特殊彈道完成后魚雷在水平面上前進的距離、位置點偏離原航向的角、航向偏離原航向的角、航速以L,,C,V表示。 一次轉角射擊即二次轉角等于0的二次轉角射擊。無論一次轉角射擊或二次轉角射擊, 總假設魚雷完成特殊彈道后直航距離H, 遮蓋中心與瞄準點滿足無誤差的相遇條件,H≥0 為一個預設定參數。射擊參數的計算是為了達到無誤差條件下使遮蓋中心與瞄準點相遇的目的, 相遇時刻魚雷航向的反方向相對目標航向的角稱為命中角。 若給定相遇態勢, 以表示預定命中角, 一般只能用二次轉角射擊實現。若不給定相遇態勢, 以=?表示, 可用一次轉角射擊實現遮蓋中心與瞄準點的相遇, 無誤差條件下的命中角由射擊態勢及魚雷彈道邏輯決定。 2為1,的函數, 若不限制二次轉角范圍, 則可取 此函數關于1連續可導, 且¢2(1) = –(), 其中 二次轉角射擊參數計算的輸出參數主要有一次轉角1、二次轉角2、二次轉角時刻2或對應的魚雷航程、執行特殊彈道時刻t或對應的魚雷航程、特殊彈道結束時刻t¢或對應的魚雷航程、無誤差及自導運動假設下遮蓋中心與瞄準點相遇時刻以及魚雷到達目標航向線的時刻t或魚雷航程等。輸入參數有: 1) 射擊態勢(,,,,X)、發射延遲-0; 2) 潛艇觀測站到魚雷出管位置點的距離0、魚雷彈道參數V1,1,,1,(V1,V),(V1,V),V,2,,L,,C,V; 3) 瞄準點(,X)、遮蓋中心(R,)、預定相遇態勢(,H)。 假設無誤差條件下0時刻發射的魚雷于時刻到達位置點(), 同時遮蓋中心與瞄準點以預定相遇態勢相遇。根據前面的論述, 二次轉角射擊參數計算的關鍵是建立確定 (1,)的方程。 如圖1,時刻目標及瞄準點為 O() =e+e(5) 魚雷特殊彈道結束時刻為t¢=–H/V, 開始時刻即二次轉角結束時刻為t=t¢–, 二次轉角運動開始時刻為 2=t– |2|/2=–H/V–– |2|/2(7) 1= (0+0+)e(8) 式中:R1=V1/1。魚雷V1?V變速開始時刻為t=0+, 結束時刻為t¢=t+(V1,V), 相應的魚雷位置點為 自t¢開始, 魚雷以速率V直航, 至2時刻開始二次轉角, 于2¢時刻完成二次轉角運動, 時刻應滿足2–t¢=–_– |2|/2≥0, 其中 _=0++(V1,V) ++H/V(12) 在這一條件下,2,2¢時刻魚雷位置點為 其中,R2=V/2。t時刻魚雷位置點為 時刻魚雷位置點()遮蓋中心為 =對應的方程為 上式兩邊同除以e, 利用X與-、-與X--p為終邊相同的角, 以及esgn(x)p/2= sgn(), 可得 此為確定(1,)的方程, 時刻還應滿足條件 若滿足這些關系的(1,)一般不唯一, 應取值最小的那一組(*1,*)作為射擊參數。 記 則前面確定(1,)的方程即 = (/V)[(1) /(1)] (23) 以Im、Re表示復數的虛部、實部, 因為為實數, 所以= (/V)Re((1)/(1)), 且 Im((1)/(1)) = 0 (24) 此為一次轉角1所滿足的方程。若限制1?(–3p/2, 3p/2 ), 則(*1,*)為 min= (/V)Re[(1)/(1)] s.t.(1)≥_+ |2(1) | /2 (1) = Im[(1) /(1)] 1?(– 3p/2, 3p/2) (25) 的解, 射擊參數存在的條件為*<¥, 這就是給定相遇態勢的二次轉角射擊參數模型。 函數(1)在 (–3p/2, 3p/2)內一般有3個0點, 滿足要求的不超過2個, 一般只有1個, 因此解這個優化問題的關鍵是解方程(1) = 0。 式中, 起點11可取[,]的左或右端點, 迭代結束條件為|1n|≥3p/2, 或|(1n)|≤, 或≥N, 對于= 10– 15的情形, 可取最大迭代次數N= 10。 函數(1)導數的計算公式為 函數(1)的公式中符號函數及絕對值函數的導數以其廣義導數表示, 即sgn¢() = 2(), ||¢= sgn(),()為Dirac-函數。則 利用這些公式可以實現¢(1)的計算。 若1= 0, 則魚雷出管后不進行一次轉角, 可稱為直進射擊, 射擊方向為潛艇航向, 這個航向相對采用目標運動要素時刻目標方位線的角= rb(–) = –X稱為直進射擊的提前角。 對于不預設相遇態勢的情形,2= 0, 魚雷發射后將一直直航。在前面的公式中令1=2= 0,X= –, 可得 記 則 所以 式中,滿足方程|(V/)+|2= |– (/)|2, 即 即不預設相遇態勢的直進射擊提前角及相遇時刻可用上述解析公式計算。 為驗證以上公式及算法的正確性, 對于用以上方式計算的射擊參數, 可以用動畫形式顯示各時刻潛艇、魚雷、目標的位置及航向, 關鍵是(*1)時刻遮蓋中心與瞄準點是否重合且滿足預定相遇態勢。下面設定一個特殊彈道用于測試, 假設自t時刻開始, 魚雷以速率V直航l, 之后直航變速至V, 變速運動的時間為(V,V), 航程為(V,V), 之后以角速率轉向, 轉向運動完成后直航l, 然后轉以角速率轉向, 轉向運動完成后直航l。 數值實驗發現, 以上這些公式及算法是正確的, 考慮到(1)/(/V) 與(1)有相同的符號與極值點, 且(1),¢(1),(1)/(/V)是無量綱的, 為便于直觀理解求解1*的算法, 可以將它們的圖像畫在以1為橫坐標(單位為度)縱坐標無量綱的一個直角坐標系內, 其典型圖像見圖2。 圖3為另一次實驗的至*時刻的魚雷彈道平面圖, 輸入參數為:=19kn,= 50°,= 50 cab,0= 2 s,X= 50°,= 5 kn,0= 25 m,= 100 m,= 20 s,V1= 25 kn,1= 10°/s,1= 15°/s,l=l=l= 500 m,= – 50°,= 100°,=15°/s,V= 50 kn,= 1000 m,X= –90°,R= 938.9574 m,= –45°,H= 1000 m,= –150°, 假設魚雷的變速運動為加速率0.5 m/s2的勻變速直線運動。計算的射擊參數為1*= 62.7804°,2*= 91.2196°,*= 515.5107 s。畫圖所用初始方位= 0, 這些參數的選取只是為了驗證公式及算法, 并非出于實用的目的。改變相關參數, 可以產生比較復雜的態勢。 圖2 計算射擊參數的圖像 圖3 魚雷彈道平面圖 兩雷平行航向齊射的目的是實現無誤差條件下魚雷二次轉角完成后的航向線平行且各雷分別命中“目標”的艦艏及艦艉, 所謂“目標”是指一段抽象的區域, 其長度為目標或目標及其尾流長度的一定倍數。在不考慮魚雷變速、變向、變深等條件下, 有一組傳統的計算兩雷一、二次轉角等射擊參數的公式, 文獻[2]指出, 這些公式計算的射擊參數不能實現無誤差條件下各雷分別命中艦艏及艦艉的設想[3-6]。考慮魚雷可能的變速、變向、變深等彈道過程, 必須重新設計兩雷平行航向齊射參數的計算方法。 平行航向齊射的實質是預先設定命中角的二次轉角射擊, 這個預先設定的命中角就是假想的中線魚雷一次轉角射擊的命中角, 將兩雷齊射看成兩次預定相同命中角的單雷射擊, 選擇兩條魚雷的瞄準點分別為目標艦艏及艦艉, 利用前面的方法計算射擊對數, 就可實現平行航向齊射的目的。假想的中線魚雷的射擊瞄準點及發射延遲理論上可以隨便選取, 一般可選擇目標中點作為其瞄準點, 2條魚雷發射時刻的中間時刻作為其發射時刻。 以上將潛艇魚雷轉角射擊在一般意義下進行了抽象的研究, 其目的是建立一個通用模型, 使其適用于不同射擊或攻擊方式的需求。為此對瞄準點、遮蓋中心、預定相遇態勢、特殊彈道等進行了一般的參數化描述, 這些參數的特定取值可對應于傳統的射擊參數計算方法。 利用以上模型及算法可以很簡單地編制一個動畫實驗程序, 對以上公式及算法進行驗證。有目的的設置參數的不同取值, 可以就特定的攻擊態勢對所關心的問題進行直觀地實驗研究。 用復數表示平面上的向量或點, 使公式推導十分簡潔, 不容易出錯且易于檢查, 還有利于編程實現。用支持復數運算的軟件(Matlab等), 上述計算的編程很簡單, 若用不支持復數運算但支持運算符重載的語言(VC++, VC#等)編程, 可先編寫一個支持復數運算的類, 以實現復數的相關計算。若用不支持運算符重載的語言(Ja等)編程, 或不預先編寫一個支持復數運算的類, 就需要將前面的公式改寫成虛部及實部的分量形式。為便于檢查, 這些公式中復數的實部只用余弦, 虛部只用正弦。 (1),(1)的分量形式可以很方便地給出。 Re(1) = cos1+ (/V)cos(X–) (38) Im(1) = sin1+ (/V)sin(X–) (39) ¢(1)的分量形式為 利用分量形式, 復數的輻角及大小可用arg= atan2(Im, Re), || = [(Im)2+ (Re)2]1/2計算, 復數相乘及相除對應的復數的虛部及實部可借助于輻角進行, 其公式為 Im(12) = |1||2|sin(arg1+ arg2) (42) Re(12) = |1||2|cos(arg1+ arg2) (43) Im(1/2) = |1||2|sin(arg1– arg2) (44) Re(1/2) = |1||2|cos(arg1–arg2) (45) [1] 李本昌, 李長文. 預定相遇態勢的潛射魚雷射擊及其技術方法[J]. 指揮控制與仿真, 2013, 35(2): 5-8.Li Ben-chang, Li Chang-wen. Firing and Technical Method Based on Given Meeting Situation of Sub-laun- ched Torpedo[J]. Command Control & Simulation, 2013, 35(2): 5-8. [2] 李長文, 王鵬. 一種新的兩雷平行航向齊射參數計算方法[J]. 潛艇學術研究, 2012, 30 (5): 46-48. [3] 夏佩倫, 劉勇, 陳志鵬. 直航魚雷齊射命中間隔的計算與分析[J]. 魚雷技術, 2010, 18(4): 308-311.Xia Pei-lun, Liu Yong, Chen Zhi-peng. Calculation and Analysis of Hit Spread for Straight Running Torpedo Salvo[J]. Torpedo Technology, 2010, 18(4): 308-311. [4] 李本昌, 梁濤. 尾流自導魚雷的齊射及其建模[J]. 火力與指揮控制, 2008(6): 128-130. Li Ben-chang, Liang Tao. Method and Model on Salvo Launching Wake-guided Torpedoes[J]. Fire Control & Command Control, 2008(6): 128-130. [5] 趙正業. 潛艇火控原理[M]. 北京: 國防工業出版社, 2003. [6] 張靜遠. 魚雷作戰使用與作戰能力分析[M]. 北京: 國防工業出版社, 2005. General Model and Algorithm of Two-time Turn Angle Shooting of Torpedo for Predetermined Encountering Situation LI Chang-wen, LI Ben-chang, CHU Lei (Office of Science Research Department, Navy Submarine Academy, Qingdao 266042, China) To compute the parameters of two-time turn angle shooting of a torpedo for predetermined encountering situation, a general model satisfying the requirements of different shooting modes is constructed by considering possible special trajectory and torpedo velocity change. The formulas for Newton iteration algorithm are given. The correctness of the proposed model and algorithm is validated by numerical experiment, and the results indicate that the model and algorithm can satisfy the computation requirements of the shooting parameters for straight running, acoustic homing, wake homing, salvo, target selection, etc. torpedo; predetermined encountering situation; two-time turn angle; shooting parameter TJ630 A 1673-1948(2012)04-0306-07 2013-04-25; 2013-05-11. 李長文(1962- ), 男, 副教授, 研究領域為軍事運籌. (責任編輯: 許 妍)1.4 魚雷彈道邏輯及參數假設
1.5 預定相遇態勢
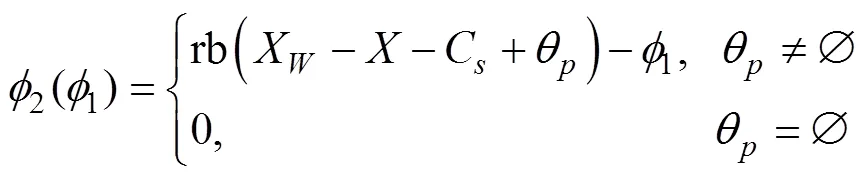
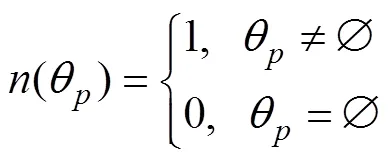
1.6 二次轉角射擊輸入輸出參數
1.7 二次轉角射擊的描述模型



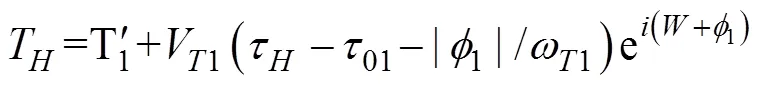

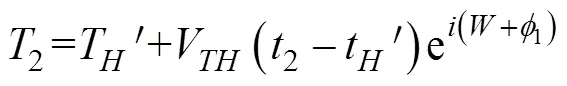
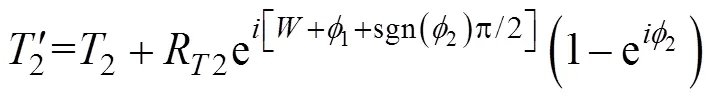
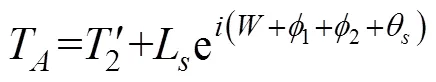



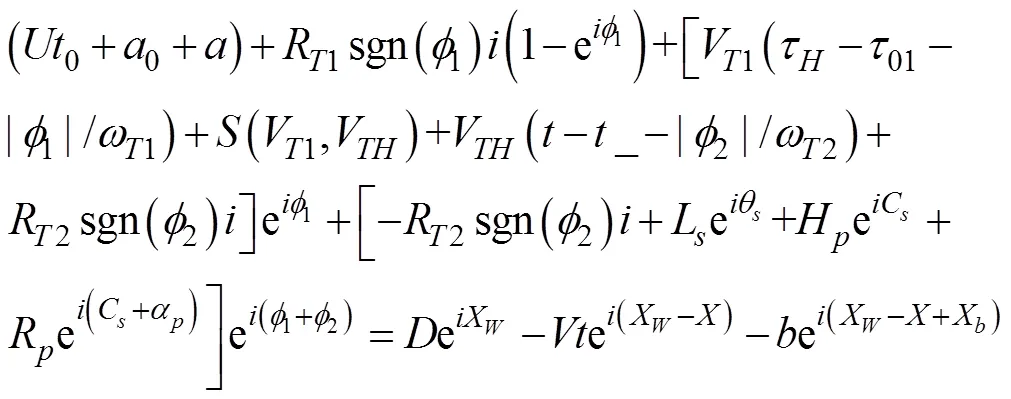
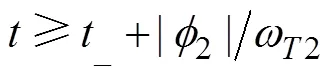
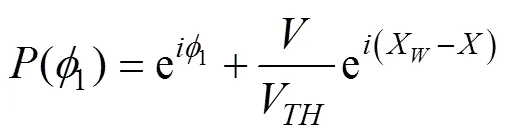
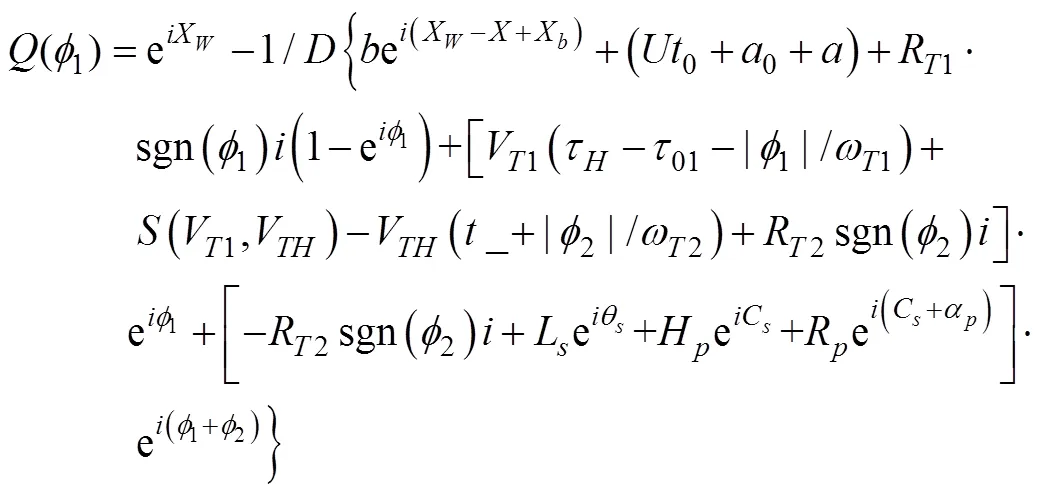
2 射擊參數計算方法
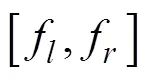
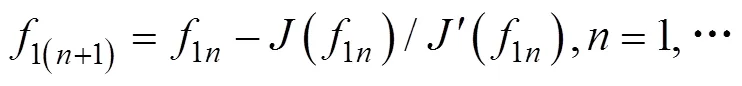
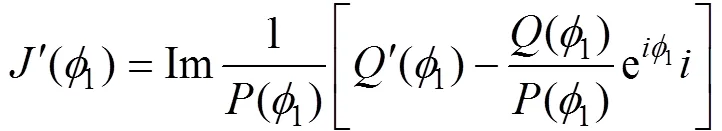

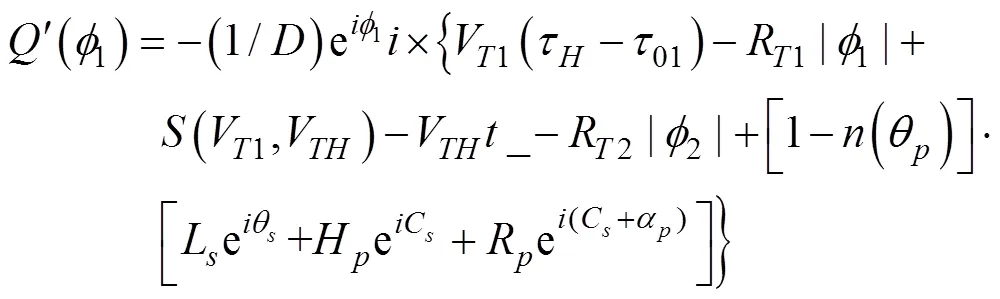
3 不預設相遇態勢的直進射擊提前角
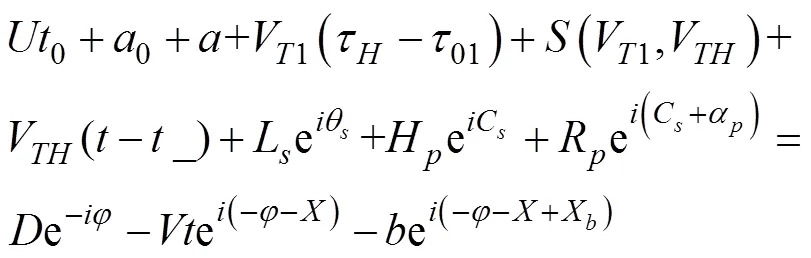
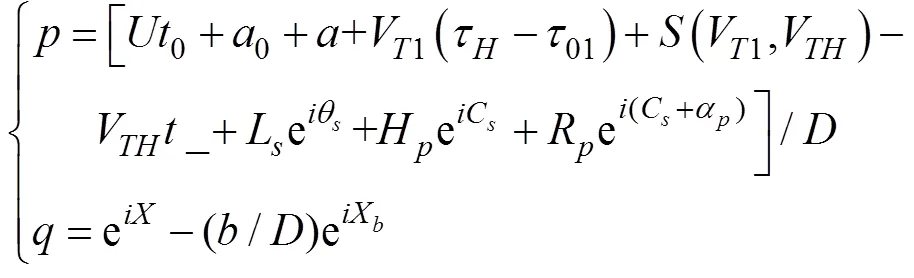
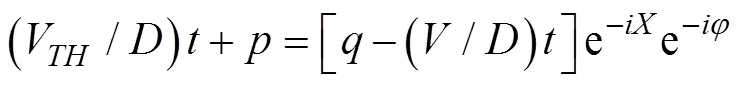


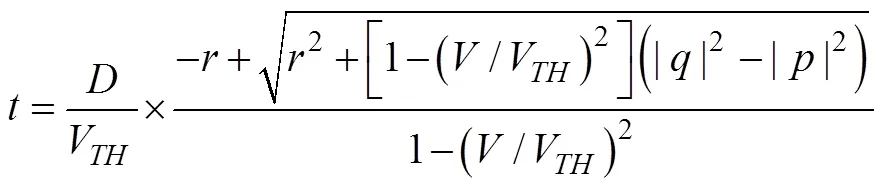
4 公式驗證及算法實驗

5 平行航向齊射參數的計算
6 結束語





