高速鐵路測量中高斯平面坐標與斜軸墨卡托平面坐標的轉換

田林亞，祖力比亞·阿布都熱西提，張勇，熱比亞·依馬爾

(河海大學地球科學與工程學院，南京 210098)

近些年來，中國的高速鐵路建設得到了快速的發展。高速鐵路作為一種精密工程，對工程測量各個環節都提出了更高的要求。例如，根據《客運專線無砟軌道鐵路工程測量技術暫行規定》的技術要求，高速鐵路測量的平面坐標系應采用獨立坐標系，建立坐標系時應滿足投影的長度變形不超過10 mm/km。對于大致呈東西走向的線路來說，如果采用高斯投影方法建立獨立坐標系，就需要劃分多個投影帶進行投影才能滿足上述要求，這樣就產生了多個獨立的坐標系，產生了坐標系不統一和鄰帶坐標的換算等問題。如果采用斜軸墨卡托投影方法建立坐標系，投影時將圓柱面相切于線路中心線附近，這樣既可以保證投影的長度變形值不大于10 mm/km，且可以獲得統一的坐標系。本文主要研究高斯平面坐標向斜軸墨卡托平面坐標的轉換模型，并結合實際工程數據進行計算與分析。

1 由高斯平面坐標計算斜軸墨卡托平面坐標的模型

墨卡托投影是一種保角圓柱投影，它以圓柱作為投影面，將經緯線先投影到圓柱面上，再將圓柱面展開成平面。圓柱面與地球相切，當切線處于斜位的狀態下時便為斜軸墨卡托投影，如圖1所示。

圖1 斜軸墨卡托投影

采用斜軸墨卡托投影時，如果把地球視為橢球，計算過程將極其繁瑣與不便，在幾百千米的范圍內把地球視為半徑相同的圓球是可行的，如果線路太長，則可以采用分段處理的方法。值得注意的是，在大范圍內把地球看做圓球來處理所產生的誤差將是不容忽略的。

1.1 投影圓球體的選取

斜軸墨卡托投影中，投影圓球的定位應滿足:參考圓球體的中心位于國家空間直角坐標系的Z軸上;定向應滿足參考圓球體三維坐標系的Z軸與國家空間直角坐標系的Z軸重合，X軸和Y軸分別與國家空間直角坐標系的X軸和Y軸平行。

設線路中某個已知點在國家坐標系中的高斯平面坐標為(B，L)，由高斯投影反算公式(1)可計算該點在國家坐標系中的大地坐標(B，L)。

式中，l為經差，Bf為垂足緯度，ηf、tf分別為按 Bf值計算的相應量。

再根據式(2)，由該點的國家大地坐標(B，L，H)計算其空間直角坐標(X，Y，Z)。

現假設參考圓球體中心O'位于國家參考橢球中心O下方，如圖2所示，O'O的長度為S，那么線路上該點在以O'為原點的空間直角坐標系中的坐標為(X，Y，Z+S)。定義圓球的半徑為 R，R根據式(3)計算得到。

圖2 參考圓球體示意

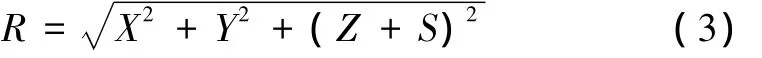
根據式(3)可列出如下誤差方程式

式中，S0和 R0分別為 S和 R的初始值，R0

當線路中有2個以上已知點時，可通過最小二乘法求得dS和dR，從而計算出S和R。

1.2 計算任意一點相對于參考圓球體的大地坐標

因為地球參考圓球的定向、定位與地球參考橢球的定向、定位原理是一樣的，所以在計算任意一點位于參考圓球體上的大地坐標(φ1，λ1，H1)時，可采用式(6)計算得到。

式中，φ1為緯度，λ1為經度，H1為大地高。

1.3 計算任意一點相對于圓球體和斜軸的大地坐標

如圖3所示，假設AB為線路走向上的兩點。首先在球面上建立以A點為極點、以AP為極軸的球面坐標系，根據球面三角公式可推得式(7)，并可計算出線路上任意一點的極坐標(θ，ρ)。

圖3 斜軸投影大地坐標計算示意

其次，確定斜軸圓球。以過AB的大圓弧為中央子午線，則沿線任意一點各點在斜軸圓球上以A為極點、AB 為極軸的極坐標 θ'和 ρ'為

式中，θB為B點的 θ坐標。

最后，計算任意一點在斜軸圓球上的大地坐標。取極點A為工程獨立坐標系的原點，則極點A在斜軸圓球上的經緯度為(0，0)。根據球面三角公式可得到由極坐標計算大地坐標的計算公式:

式中，(φ2，λ2)為所求點在斜軸圓球上的經緯度。

1.4 參考圓球體的投影正算

投影正算就是根據投影條件將參考圓球面上的大地坐標(φ2，λ2)換算成投影面上的平面坐標(xm，ym)。基于斜軸圓球體的投影正算與高斯投影正算類似，等角投影的條件是

式中，r為平行圈半徑，M為卯酉圈半徑。當投影球體為圓球時，其條件式可表達為

參考高斯投影正算公式，由于 xm是經度差λ2的偶函數，ym是λ2的奇函數，可假設

其中，a0、a1、a2、a3…為只包含 φ2的函數，且 φ2、λ2應化為弧度形式，對式(12)求偏導得

將式(12)、式(13)分別代入式(10)中，由于在起點處有λ2=0，則點(0，φ2)投影后的平面坐標為(R·φ2，0)，即 xm=a0=R·φ2，因此解得各個系數為

式中，(φ2，λ2)為所求點在斜軸圓球上的經緯度，R為圓球半徑。將上述系數代入式(11)，便可求得任意一點的斜軸墨卡托平面坐標(xm，ym)。

2 實例計算與分析

如圖4所示，設某條高速鐵路線路長400 km，寬15 km，大致呈東西走向，首級平面控制網中的6個控制點采用GPS測量，并將測量成果轉換為北京54坐標系中的平面坐標，為了控制投影的長度變形值不大于10 mm/km，分成6個高斯投影帶進行投影，其高斯平面坐標及投影變形見表1。

圖4 線路及控制點略圖

表1 高斯平面坐標及投影變形

從表1數據可以看出，將線路首級平面控制網分成6個投影帶進行投影和平差計算，每個控制點到相應投影帶中央子午線的投影長度變形都小于10 mm/km，滿足了有關高速鐵路測量規范的要求，但是分成6個投影帶分別進行投影計算，就形成了6個獨立平面坐標系，產生了坐標系不統一的問題，在相鄰點的綜合使用過程中，不僅需要頻繁的換帶計算，還可能存在較大的投影變形。

如果采用斜軸墨卡托投影方法來建立平面坐標系，并且取點 ZX1為起點，取點 ZX6為終點，取點ZX1和點ZX6所在圓弧為斜軸墨卡托的投影中線，根據本文探討的坐標轉換方法和流程，采用C號.NET編寫相應的坐標轉換計算程序，將表1中的高斯平面坐標換算成斜軸墨卡托平面坐標，結果見表2。

表2 斜軸墨卡托平面坐標及投影變形

從表2的數據可以看出，斜軸墨卡托投影產生的長度變形遠小于高斯投影產生的長度變形。ZX5距離投影中線的距離為12 km，投影變形最大，但是遠小于10 mm/km。采用斜軸墨卡托投影，這6個控制點同屬一個坐標系，坐標系也得到了統一。

另外，對斜軸墨卡托投影進行有關計算表明:當線路長度為幾百千米時，為了使所有的投影變形小于10 mm/km，線路至投影中線的最大橫向距離應小于25 km;如果線路長度達到幾千千米或者最大橫向距離超過25 km，應該將線路分成幾段進行投影，且相鄰投影帶之間應有適當的重疊區域。

3 結論

對于呈東西走向的高速鐵路，在建立平面坐標系時應特別注意投影的長度變形問題。當線路較長時，為了控制長度投影變形，可以采用高斯分帶投影，但也因此產生了坐標系不統一問題，如果分帶過多，在控制點坐標的使用中也帶來了坐標換帶計算的麻煩。采用斜軸墨卡托投影，可有效地解決高斯分帶投影導致的一些問題。

本文對高斯平面坐標向斜軸墨卡托平面坐標的轉換模型進行了研究，詳細地闡述了坐標轉換的方法及其流程。對某條長約400 km的高速鐵路測量數據，先采用高斯分帶投影的方法進行控制點坐標及投影變形的計算，認為分6個帶投影可以滿足投影變形不大于10 mm/km的要求，但同時也產生了6個獨立坐標系。采用斜軸墨卡托投影和本文研究的坐標轉換方法，不僅顯著地減小了投影變形，也將6個高斯帶中的坐標轉換到1個斜軸墨卡托投影帶中，使6個控制點的坐標系統得到了統一。計算、分析和實際應用表明，本文研究的方法是正確的。

［1］盧建康，劉華.高速鐵路精密工程測量技術體系的建立及特點［J］.鐵道標準設計，2010(S1):70-73.

［2］李全海.斜圓柱投影及其對 GPS空間坐標的轉換模型［J］.同濟大學學報，2002(1):106-110.

［3］陸鵬程，林冬偉.斜軸墨卡托投影模型及其應用分析［J］.鐵道勘察，2010(4):26-29.

［4］呂慧玲.斜軸墨卡托投影方法在鄭西客專中的應用研究［J］.測繪信息與工程，2009(34):26-28.

［5］陳光金.鐵路精測網對橋隧施工測量的影響分析［J］.鐵道標準設計，2010(S1):82-84，117.

［6］王衛紅，劉云東.武廣客運專線滿足無砟軌道控制測量的方案探討［J］.鐵道標準設計，2006(S1):197-200.

［7］李曉娥.任意帶高斯正形投影平面直角坐標系統在武廣客運專線勘測設計中的應用［J］.鐵道標準設計，2006(S1):195-196.

［8］郭紀明，孔元祥.控制測量學(上下冊)［M］.武漢:武漢大學出版社，2007.

［9］張正祿，等.工程測量學［M］.武漢:武漢大學出版社，2005.

［10］王解先，伍吉倉，高小兵.斜軸墨卡托投影及其在高鐵建設工程中的應用［J］.工程勘察，2011(8):69-72.

［11］李付偉，劉靈杰，王曉智.斜軸墨卡托投影的長度變形分析［J］.河南科技，2012(2):80-81.

［12］劉家臣.高速鐵路精密工程控制測量精度研究［J］.測繪與空間地理信息，2011(12):216-218.