鐵路曲線限界加寬研究
周兵和
(中鐵第四勘察設計院集團有限公司線站處,武漢 430063)
1 限界加寬有關規定及存在問題
1.1 曲線限界加寬有關規定
(1)《鐵路技術管理規程》對鐵路曲線地段限界加寬值的計算公式及加寬方法規定為
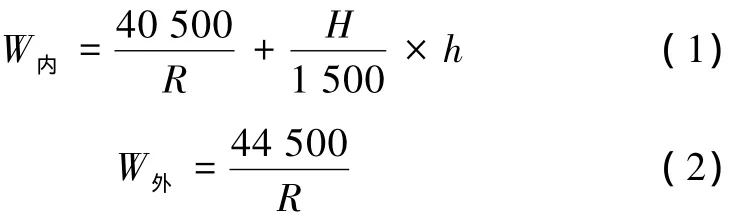
式中 R——曲線半徑,m;
H——計算點距軌頂高度,mm;
h——外軌超高,mm。
(2)《鐵路技術管理規程》及《高速鐵路設計規范(試行)》規定:曲線上建筑限界的加寬范圍,包括全部圓曲線、緩和曲線和部分直線,采用階梯加寬方法,即緩和曲線中點前13 m至緩圓點之間加寬值規定為與圓曲線地段相同,緩和曲線中點前13 m至直緩點前22 m之間加寬值規定為圓曲線地段加寬值的二分之一。
(3)《站場與樞紐》對無緩和曲線的曲線變加寬地段的加寬值計算方法為
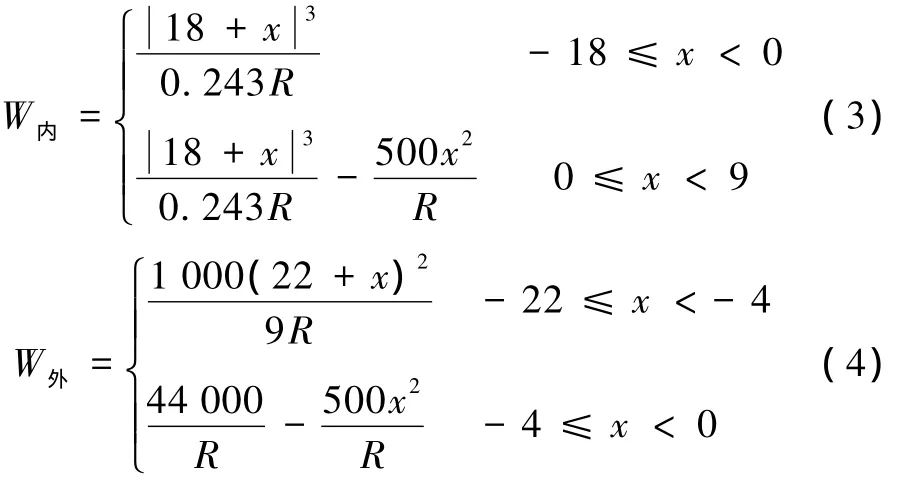
式中 R——曲線半徑,m;
x——計算點位置,直圓點為0點,m。
1.2 現有加寬規定存在的問題
(1)緩和曲線、緩和曲線與曲線、緩和曲線與直線間的變加寬范圍無適用的計算公式。
(2)階梯加寬法沒有體現變加寬地段的加寬規律,規定的結論偏于粗簡,部分地段冗余值過大。
(3)階梯加寬法不能滿足個別控制點限界精確計算的要求。
(4)階梯加寬法不能適應曲線站臺間距加寬設計要求。階梯狀站臺難被各方認同,且將導致站臺間距冗余過大,不必要地加大車體與站臺間隙。
(5)無緩和曲線的站內曲線加寬值的計算公式,未考慮與超高加寬的綜合,且其線型復雜,在工程設計中應用性不是很強,存在簡化的空間。
有緩和曲線或無緩和曲線的鐵路曲線的限界加寬,在現有規范中過于籠統,在工程設計中容易引起困擾,有必要進行深入研究,形成可供參考的加寬方法和計算公式。
2 影響曲線限界的因素
曲線地段影響限界加寬的因素有曲線超高、曲線半徑和軌距加寬。
(1)曲線軌距加寬:《鐵路技術管理規程》規定,曲線軌距加寬值在 R<300 m時為15 mm,R<350 m時為5 mm,R在350 m及以上時,軌距加寬為0 mm。可知軌距加寬發生在 R<350 m的曲線,且加寬值較小,對限界加寬的影響很小,一般都忽略該因素的影響。
(2)超高加寬:曲線超高地段,外側軌面高于內側軌頂,車體向曲線內側傾斜,產生限界加寬。曲線內側,超高加寬為正值,且與計算點高度成正比。曲線外側,超高加寬為負值,負加寬值最大值(絕對值最小)發生在車底板處。
(3)曲線加寬:車輛中心線由前后輪軸點位控制,曲線地段車體中心線與線路中心線不一致,前后輪軸之間車體向曲線內側偏移,車體兩端向曲線外側翹出。因曲線地段車輛中心線的偏移產生的加寬簡稱曲線加寬。在圓曲線范圍,內側加寬最大值發生在車體中心點處,外側加寬最大值發生在車體兩端。
3 內側限界加寬分析
3.1 有緩和曲線時內側限界加寬分析
3.1.1 緩和曲線前后內側超高加寬分析
在緩和曲線地段、由無超高地段駛入緩和曲線地段、以及由緩和曲線地段駛向圓曲線地段期間,車輛前后輪位置的超高值不相同,車體前后傾斜不一致,后輪處加寬值最小,前輪處最大,之間呈線性遞增關系。
車輛由無超高~變超高~恒定超高地段的過程中,前后輪間車體因側傾引起的偏移量的幾何位置不斷發生偏移,如圖1所示。
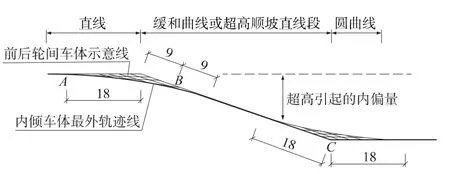
圖1 曲線上車輛偏心加寬示意(單位:m)
可分三段來對內側超高加寬值進行計算。
第一段:A點至B點,即緩和曲線起點前18 m、后9 m,用直線AB來近似表達。
第二段:由 B點至 C點,加寬值線性增加至最大值。
第三段:C點之后,超高加寬值穩定為最大值。
計算公式為
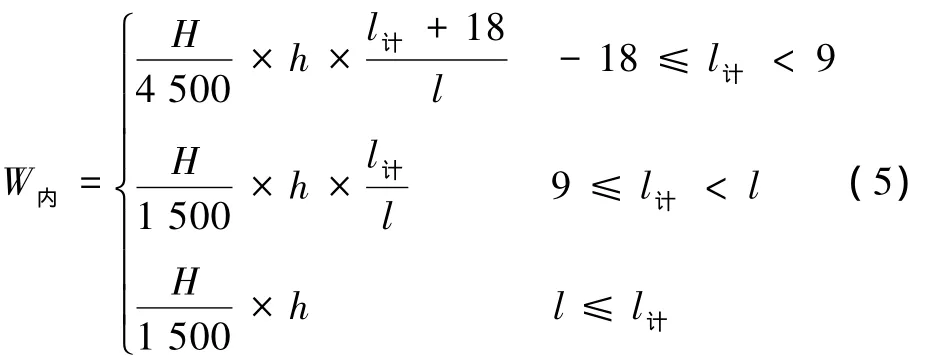
式中 R——曲線半徑,m;
l——緩和曲線長,m;
h——曲線超高,mm;
l計——計算點位置,m。
3.1.2 緩和曲線前后內側曲線加寬分析
圓曲線地段,內側偏移量穩定不變,但在緩和曲線地段,以及直緩點、緩圓點前后,內偏量值隨曲率半徑不斷變化。通過在R-1 000 m、l-120 m曲線上的運行模擬,得出內側加寬值及分析圖表,詳見表1和圖2。
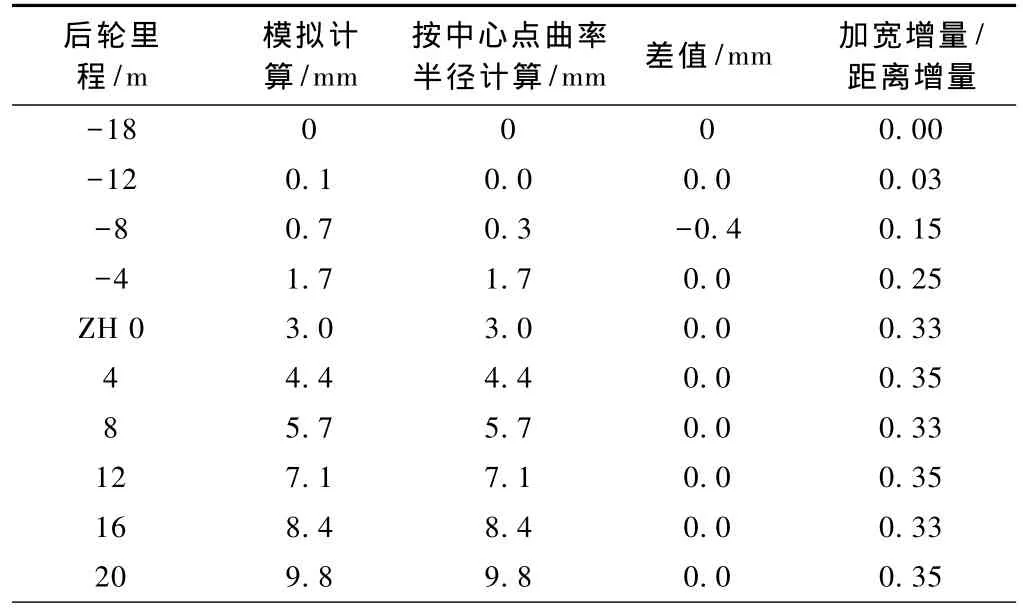
表1 曲線內側加寬值模擬計算及結果分析
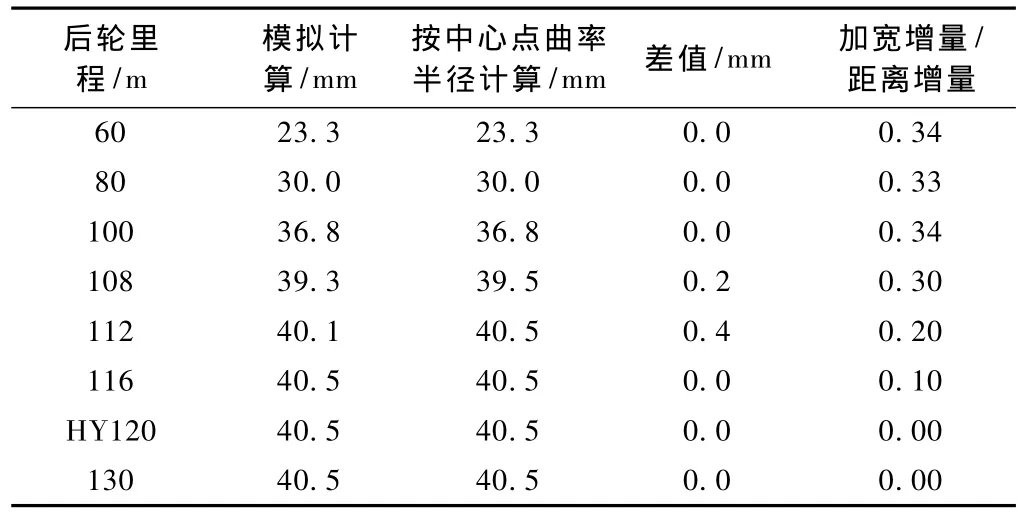
續表1
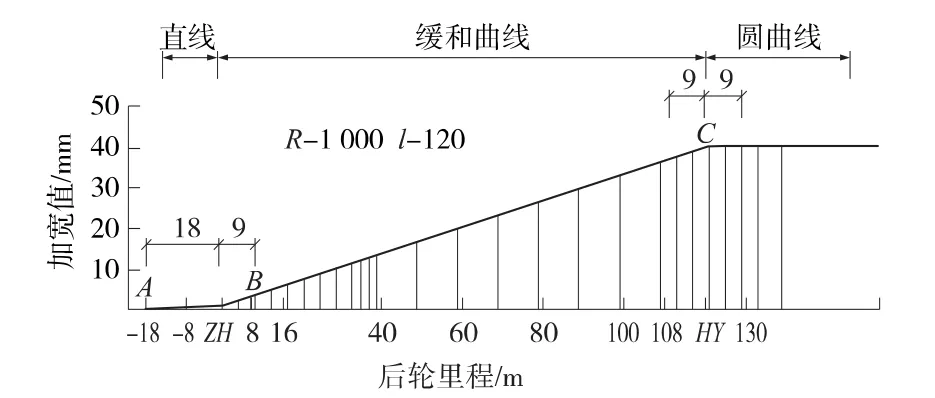
圖2 車輛內側加寬值分布示意(單位:m)
結合以上圖表,得出緩和曲線前后加寬值可按如下三段來確定。
第一段:A點至B點,即前輪進至直緩點~后輪進至直緩點期間,加寬值呈凹形曲線分布,且加寬值較小,示例結果B點加寬值小于7 mm。為簡化計算,用直線AB來近似表示。
第二段:B點至C點。B點~C點之前9 m(軸距的1/2)期間,加寬值隨里程線性增加,經圖形分析,該加寬值可近似為車輛中心處曲率半徑的加寬值,模擬計算結果證實其差值基本為0 mm。C點前9 m范圍加寬值呈一凸形曲線,近似用其切線邊來表示。故該B點~C點范圍的加寬值可用直線BC來近似表示。
第三段:C點之后,即車輛中心進入緩圓點后,可用以C為起點的水平線來表示。
計算公式為
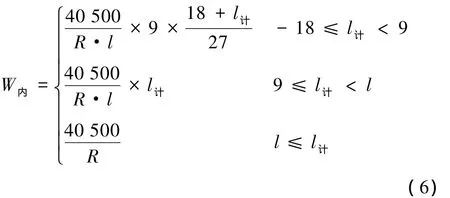
式中 R——曲線半徑,m;
l——緩和曲線長,m;
h——曲線超高,mm;
l計——計算點位置,m。
3.1.3 有緩和曲線時內側限界綜合加寬
綜合以上內側超高加寬和緩向曲線前后的內側曲線加寬分析,有緩和曲線時鐵路曲線內側綜合加寬可按以下三段進行計算。
第一段:前輪進至直緩點~后輪進至直緩點期間,綜合加寬值均從0 mm開始線性遞增。
第二段:后輪進至直緩點~車輛中心進入緩圓點期間,綜合加寬線性遞增至最大加寬值。
第三段:車輛中心進入緩圓點之后,綜合加寬值穩定為最大值。
計算公式為
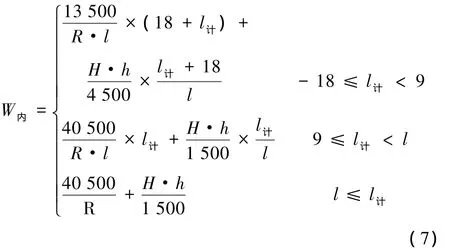
式中 R——曲線半徑,m;
l——緩和曲線長,m;
h——曲線超高,mm;
l計——計算點位置,m。
3.2 無緩和曲線時內側限界綜合加寬
無緩和曲線的鐵路曲線,其超高順坡直線段等同緩和曲線功能,可參考前述緩和曲線的分析結果進行內側加寬計算;無緩和曲線的鐵路曲線的內側曲線加寬,可參考前述《站場及樞紐》中圓曲線變加寬地段的加寬方法和公式(3)計算。兩者綜合,可分四段計算。
第一段:前輪進入超高順坡起點~后輪進入超高順坡起點期間,超高加寬值由0 mm開始線性遞增。若前輪進入圓曲線,則還需增加圓曲線引起的加寬。
第二段:后輪進入超高順坡起點~車輛中心進入直圓點期間,超高加寬值線性遞增,遞增率受超高順坡率控制。若前輪進入圓曲線,還需增加圓曲線引起的加寬。
第三段:車輛中心進入直圓點~車輛中心進至直圓點后9 m期間,超高加寬變化規律同第二段,曲線加寬值快速增加,為三次拋物線與二次拋物線的差值。
第四段:車輛中心進至直圓點后9 m之后,即后輪駛過直圓點后,曲線加寬與超高加寬穩定為最大值。
計算公式為
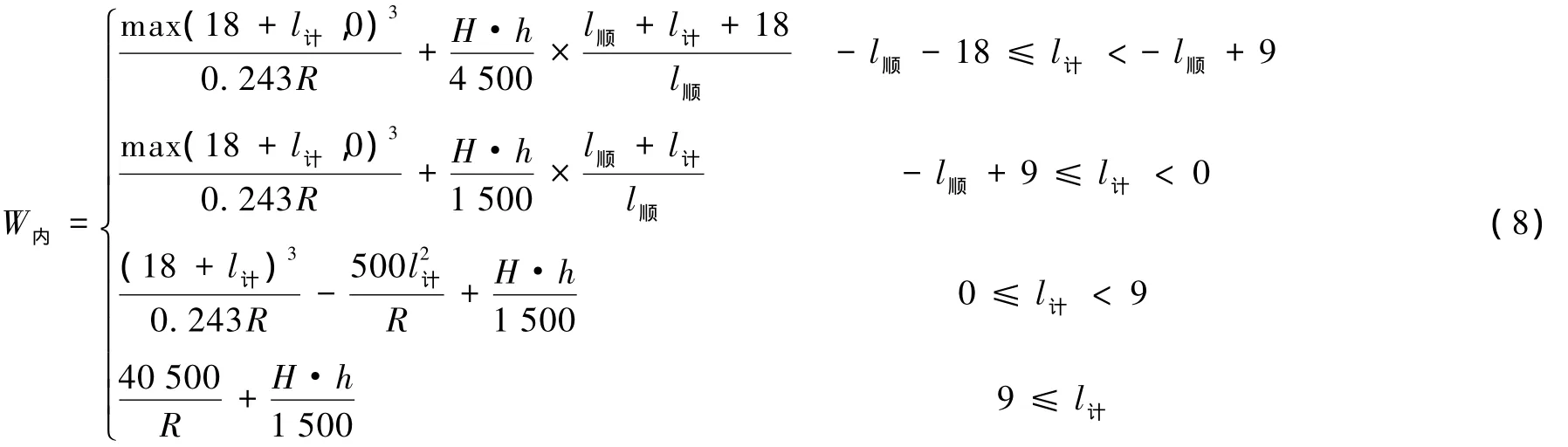
式中 R——曲線半徑,m;
l順——超高順坡長度,m;
H——計算點距軌面高度,mm;
h——曲線超高,mm;
l計——計算點位置,m。
鐵路曲線不帶緩和曲線時,一般為等級相對較低的站內聯絡線或岔后連接曲線。其超高值一般不超過25 mm。以R-800 m、超高20 mm、超高順坡長度15 m為例,疊加繪制其曲線加寬與超高加寬的分布曲線,如圖3所示。
可知順坡起點之前18 m處的A點至直圓點之前9 m處的B點(前輪處于直圓點)之間的加寬值較小且不斷增大,可用直線AB來表示;B點至直圓點之后4.5 m處C點(直圓點處于后輪與車輛中心之間中點位置)之間加寬值遞增幅度加大,可近似用直線BC來表示;C點之后,可用一水平直線來表示。示例數據中近期加寬直線的最大冗余值為+7 mm,發生在里程-5 m處。
故在允許少量冗余的情況下,無緩和曲線時曲線內側加寬公式(8)可簡化為
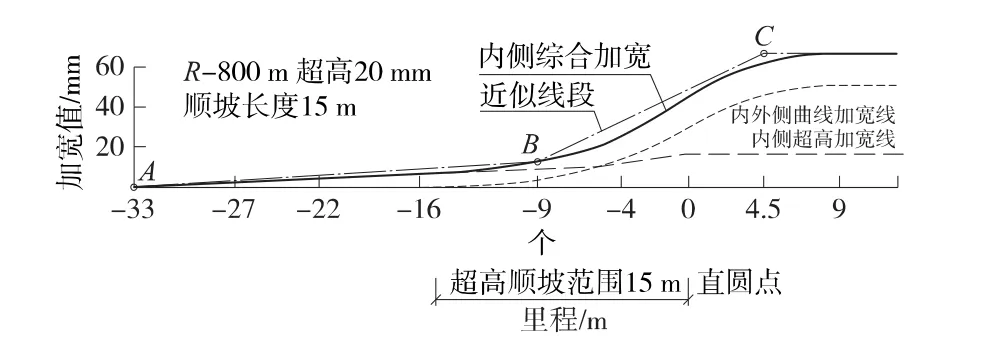
圖3 圓曲線內側加寬值分布示意
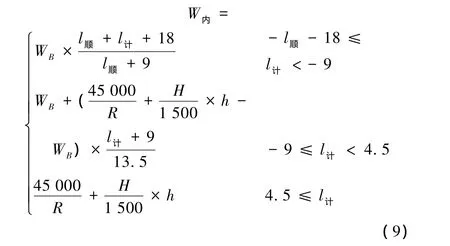
式中
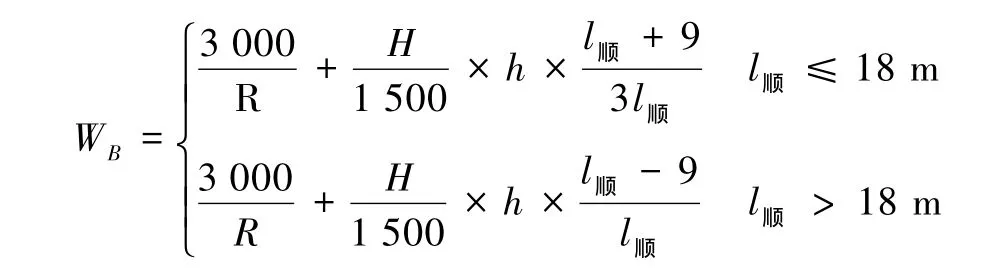
式中 R——曲線半徑,m;
l順——超高順坡長度,m;
h——曲線超高,mm;
l計——計算點位置,m。
4 外側限界加寬分析
4.1 有緩和曲線時外側限界加寬分析
4.1.1 緩和曲線前后外側超高加寬分析
外軌超高導致車體內傾,引起限界向內側偏移,對外側限界實際起到負加寬作用,因不會導致侵限,往往被忽略掉。因外側超高負加寬值隨超高值增大而增加,若一律忽略掉,將會產生較大的加寬冗余。
外側超高負加寬的最大值(絕對值最小)受車輛底板高度1 210 mm控制。
車輛頭、尾兩端外側負加寬值分別受前、后輪處超高值控制,在其由無超高~變超高~恒定超高地段運行過程中,車輛頭部和尾部超高負加寬示意如圖4所示。
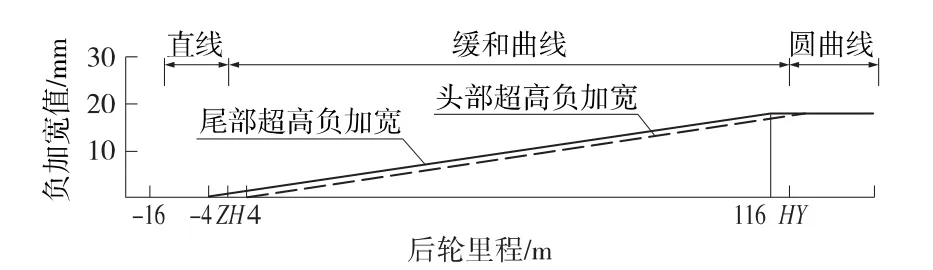
圖4 車輛頭尾超高負加寬值分布示意
從圖4可以看出,可用尾部加寬值來代表車輛的超高負加寬,公式如下
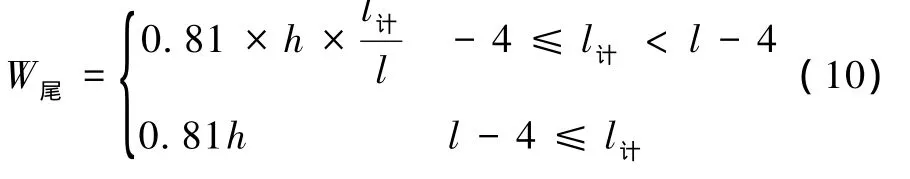
式中 h——曲線超高,mm;
l計——計算點位置,m;
l——緩和曲線長,m。
4.1.2 緩和曲線前后外側曲線加寬分析
圓曲線地段,車輛兩端外偏量相同,但在緩和曲線地段,以及直緩點、緩圓點前后,兩端外偏量值隨曲率半徑不斷變化。通過對車輛在R-1 000 m、l-120 m曲線上進行運行模擬,得出其頭尾兩端加寬值及相關的分析數據及圖表,詳見表2和圖5。
從圖5可看出,尾部加寬軌跡線包絡了頭部加寬軌跡線,可以用尾部加寬來代表外側曲線加寬,并可分三段來計算。
第一段:A點至B點,即前輪駛至直緩點~車尾到達直緩點期間,加寬值呈凹形曲線分布,且加寬值較小,為簡化計算,擬用直線AB來近似表示。
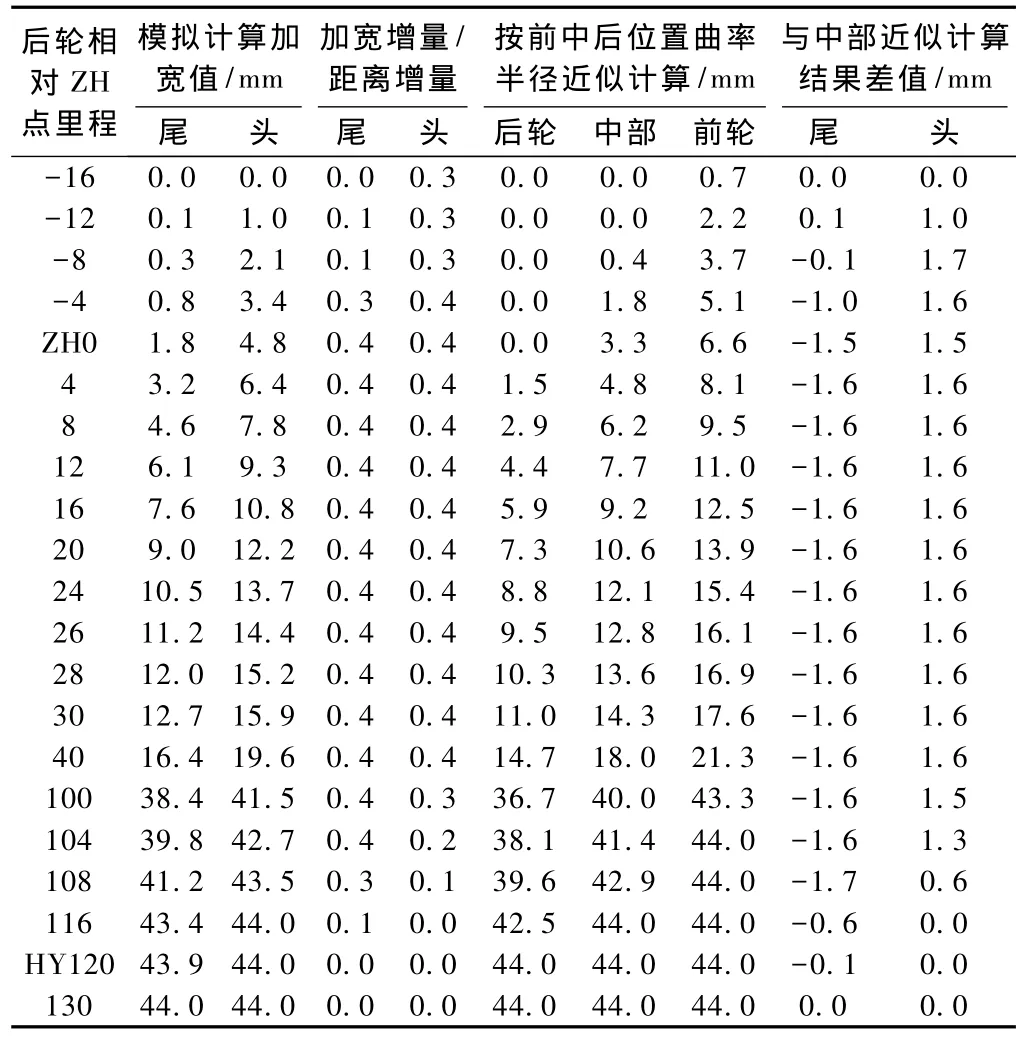
表2 外側加寬模擬計算及結果分析
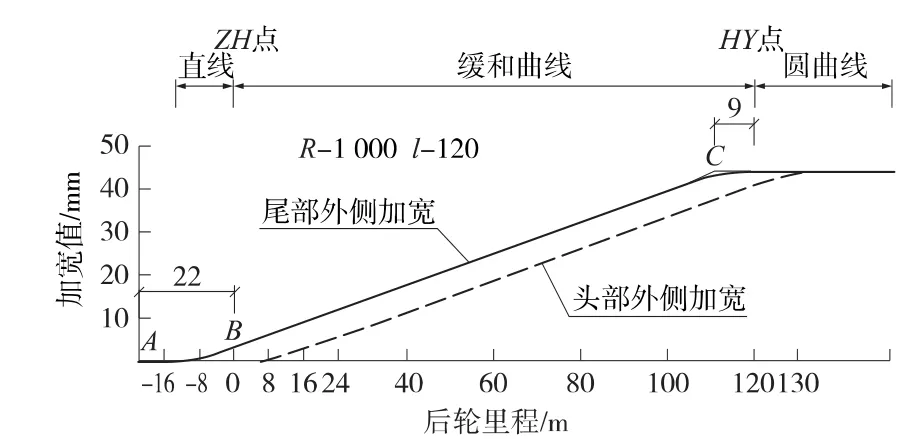
圖5 車輛頭尾外側加寬值分析示意(單位:m)
第二段:B點至C點,即車尾駛過直緩點~車尾距緩圓點9 m(軸距的1/2)期間,尾部加寬值隨車尾的位置線性增加。經幾何分析(圖6),尾部加寬值略小于車輛中心處曲率半徑的加寬值,模擬計算的示例結果顯示,該差值為1.6 mm,差值很小,故在許可少量冗余的前提下,可用車輛中心處曲率半徑的加寬來近似表示。
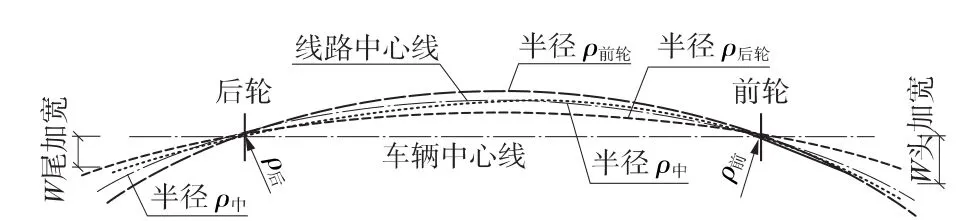
圖6 曲線上車輛偏心加寬示意
第三段:C點之后,加寬值穩定為最大加寬值。
得出加寬計算公式為
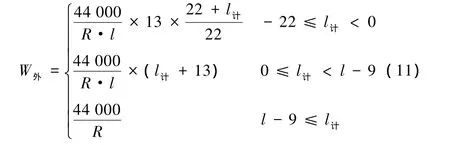
式中 R——曲線半徑,m;
l——緩和曲線長,m;
h——曲線超高,mm;
l計——計算點位置,m。
4.1.3 有緩和曲線時外側限界綜合加寬
綜合曲線外側超高加寬和曲線加寬數值及分析結果,可得出有緩和曲線時鐵路曲線外側綜合加寬值分布結果,如圖7所示。
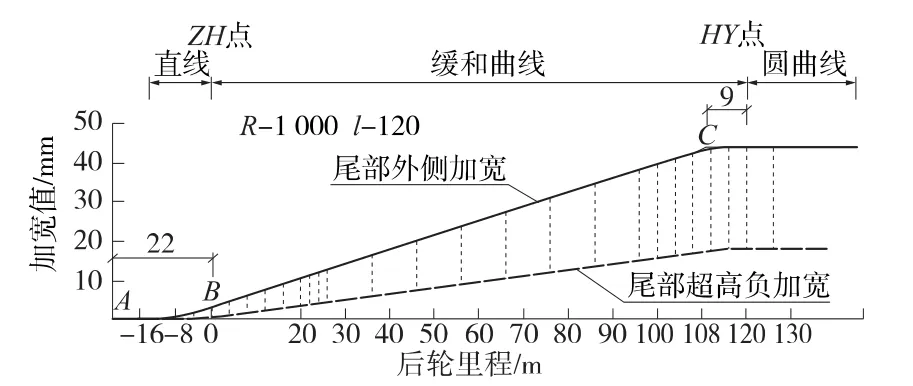
圖7 車輛外側綜合加寬值分布示意(單位:m)
第一段:前輪駛至直緩點A~車尾到達直緩點期間B,該區段無超高負加寬,只有曲線加寬,加寬值從0 mm開始線性遞增。
第二段:車尾駛過直緩點~車尾距緩圓點前9 m(軸距的1/2)期間,綜合加寬值隨里程變化線性遞增。
第三段:車尾駛過緩圓點前9 m之后,綜合加寬穩定為最大值。
各段計算公式為
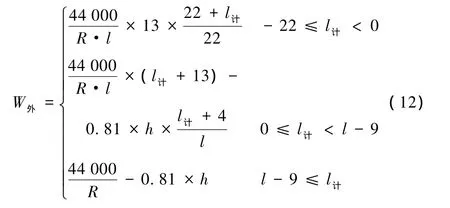
式中 R——曲線半徑,m;
l——緩和曲線長,m;
h——曲線超高,mm;
l計——計算點位置,m。
4.2 無緩和曲線時外側限界綜合加寬
無緩和曲線的鐵路曲線,其超高順坡直線段可視為緩和曲線,超高負加寬值可參考前述緩和曲線地段外側加寬方法計算。無緩和曲線的圓曲線外側加寬,可參考《站場及樞紐》圓曲線外側變加寬計算方法計算。兩者綜合,可分三段計算。
第一段:后輪進入超高順坡起點~后輪駛至直圓點期間,超高負加寬值隨里程線性遞增。期間若前輪駛入圓曲線,則還需疊加外側曲線加寬。
第二段:后輪駛過直圓點~車尾駛過直圓點期間,超高負加寬為固定值,曲線加寬值逐漸增大。
第三段:車尾駛過直圓點后,綜合加寬值穩定為固定值。
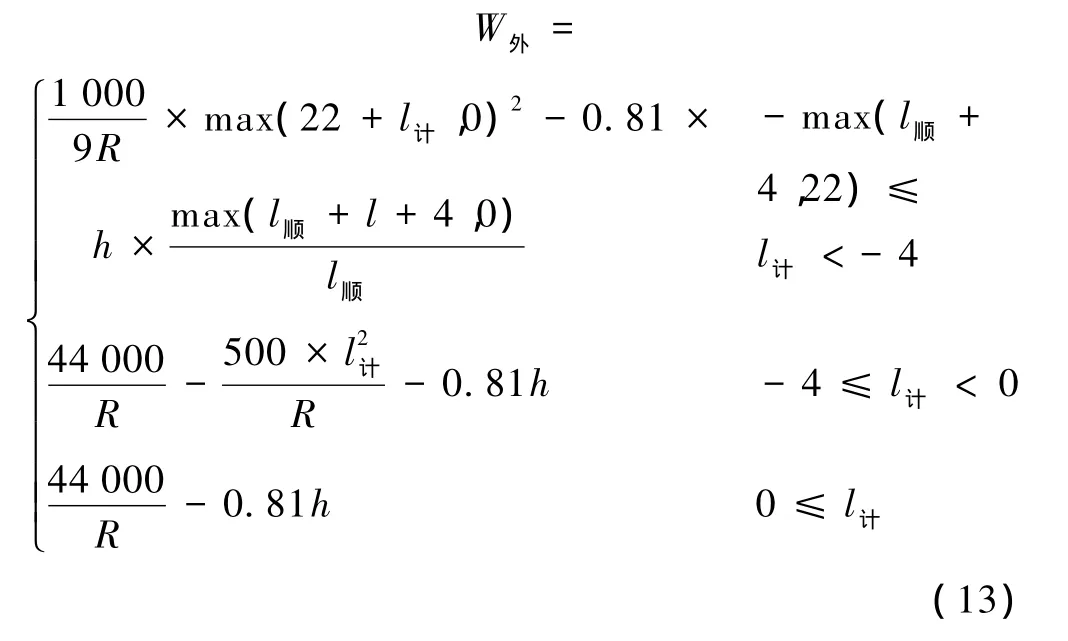
式中 R——曲線半徑,m;
l順——超高順坡長度,m;
h——曲線超高,mm;
l計——計算點位置,m。
無緩和曲線時的鐵路曲線,一般為站內聯絡線或岔后連接曲線,其超高值一般不超過25 m。以 R-800 m、超高20 mm、超高順坡長度15 m為例,疊加繪制其曲線加寬與超高加寬曲線,如圖8所示。
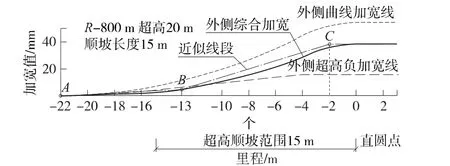
圖8 圓曲線外側加寬值分布示意
可知直圓點之前22 m處的A點至直圓點之前13 m處的B點(車輛中心處于直圓點時)之間的加寬值較小且逐漸增大,可用直線AB來近似;B點至直圓點之前2 m處的C點(直圓點處于后輪與車尾之間中點位置時)之間加寬值遞增幅度加大,可近似用直線BC來表示;C點之后,可用一水平直線來表示。近似線段產生的最大冗余值為+5 mm,發生在里程-7 m處。故在許可少量冗余、超高順坡長度不超過22 m時,無緩和曲線的鐵路曲線外側加寬公式可簡化為
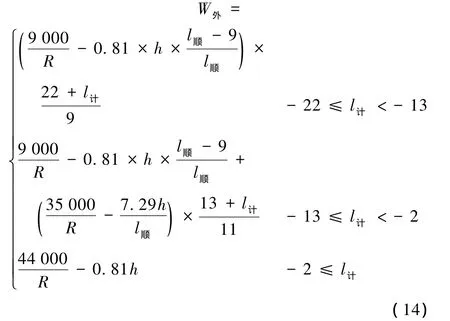
式中 R——曲線半徑,m;
h——曲線超高,mm;
l順——超高順坡長度,m;
l計——計算點位置,m。
5 曲線限界加寬研究結論
綜合曲線內側和外側限界加寬分析,歸納出曲線限界加寬辦法如下。
(1)有緩和曲線時
外側加寬:①直緩點前22 m的直線段范圍,由0 mm線性增加至Wq;②直緩點~緩圓點前9 m處的緩和曲線范圍內,由Wq線性增加至Wo;③之后緩和曲線及圓曲線地段均按Wo加寬。示意如圖9所示,計算公式見(15)、(16)。
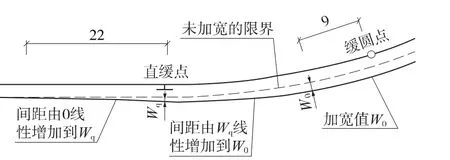
圖9 有緩和曲線時外側限界加寬示意(單位:m)
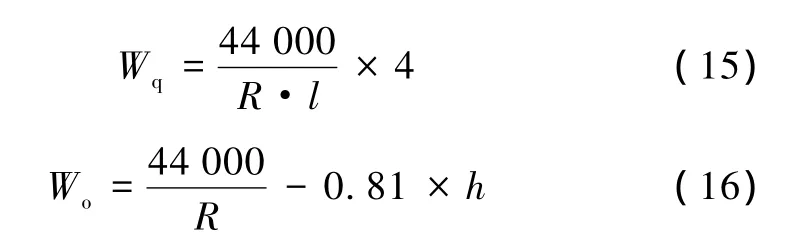
內側加寬:①直緩點之前18 m的直線段及之后4 m的緩和曲線范圍內,由0 mm線性增加至Wq;②直緩點之后4 m~緩圓點前9 m的緩和曲線范圍內,由Wq線性增加至Wo;③之后的緩和曲線及圓曲線地段均按Wo加寬。示意如圖10所示,計算公式見(17)、(18)。
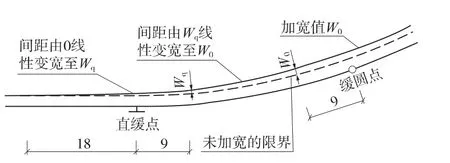
圖10 有緩和曲線時內側限界加寬示意(單位:m)
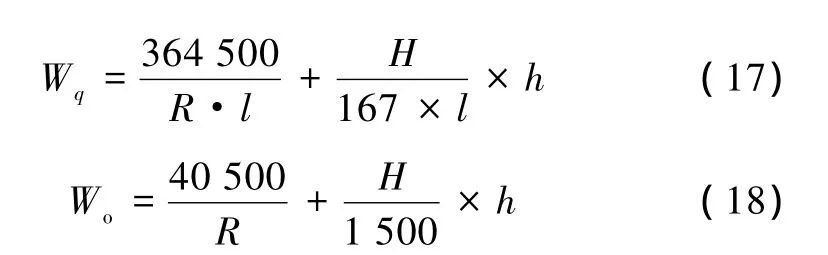
式中 R——曲線半徑,m;
l——緩和曲線長度,m;
H——計算點距軌頂高度,mm;
h——曲線超高,mm。
(2)無緩和曲線時
外側加寬值:①直圓點前22 m~直圓點前13 m的直線范圍,由0 mm線性增加至 Wq;②直圓點前13 m~直圓點前2 m的直線范圍,由Wq線性增加至Wo;③直圓點前2 m范圍內的直線以及之后的圓曲線地段均按Wo加寬。示意如圖11所示,計算公式見(19)、(20)。
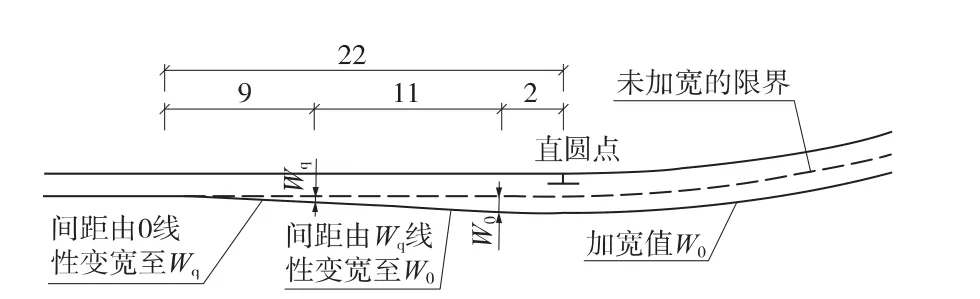
圖11 無緩和曲線時外側限界加寬示意(單位:m)
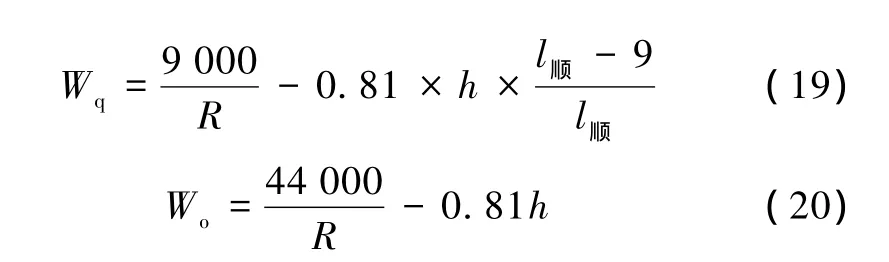
內側加寬值:①超高順坡起點前9 m~直圓點前9 m的直線范圍,由0 mm線性增加至Wq;②直圓點前9 m的直線段~直圓點后4.5 m范圍的圓曲線范圍,由Wq線性增加至Wo;③直圓點后4.5 m之后的圓曲線地段均按Wo加寬。示意如圖12所示,計算公式見(21)、(22)。
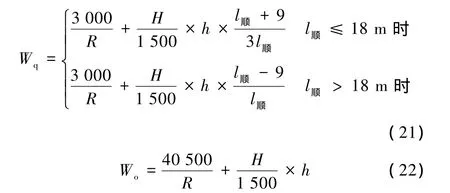
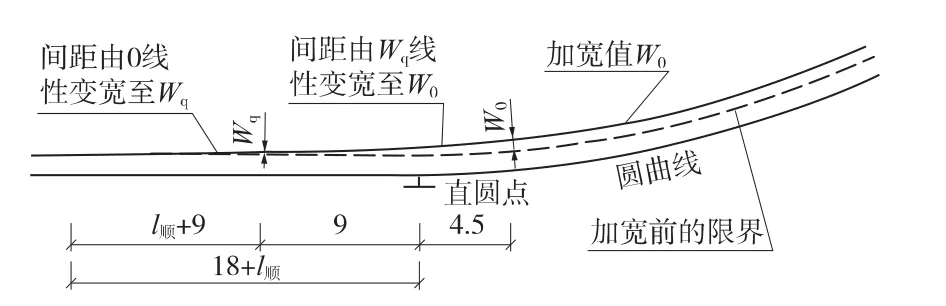
圖12 無緩和曲線時內側限界加寬示意(單位:m)
式中 R——曲線半徑,m;
l——緩和曲線長度,m;
l順——超高順坡長度,m;
H——計算點距軌頂高度,mm;
h——曲線超高,mm。
無緩和曲線時,變加寬地段留有少量冗余,如進行信號機警沖標等精度要求高的計算時,內側加寬計算可采用公式(8),外側加寬計算可采用公式(13)。
6 結語
本文對鐵路曲線限界加寬進行了深入研究,按有緩和曲線和無緩和曲線的不同情況,形成了曲線限界加寬計算的公式及示意圖,謹供鐵路工程設計人員參考。
[1]中華人民共和國鐵道部.鐵路技術管理規程[S].北京:中國鐵道出版社,2007:233-239.
[2]TB10621—2009 高速鐵路規范(試行)[S].
[3]鐵建設[2005]140號,新建時速200~250公里客運專線鐵路設計暫行規定[S].
[4]鐵建設[2005]285號,新建時速200公里客貨共線路設計暫行規定[S].
[5]GB50090—2006,鐵路線路設計規范[S].
[6]GB50091—2006,鐵路車站及樞紐設計規范[S].
[7]鐵道第四勘察設計院.鐵路工程設計技術手冊站場與樞紐[M].北京:中國鐵道出版社,2004:596-597.
[8]GB50157—2003,地鐵設計規范[S].

