半導體制造中具有重入加工工藝的雙臂組合設備的調度研究*

付 虎，伍乃騏，喬 巖

（廣東工業大學機電工程學院，廣東廣州 510006）

0 緒論

在半導體制造業中，組合設備已經被廣泛的用來加工晶圓。它是一種集成設備。因此使用組合設備，可獲得一個更具靈活性，可重構，非常有效率的加工環境[1-2]，可以帶來更高的產量[3]，縮短生產周期[3-5]，更好的利用空間[2，5]以及降低生產成本[5]。由于空間的限制，一臺組合設備由幾個加工模塊（processing module，PM）、一個傳輸模塊（transport module，TM，機械手）和兩個真空鎖（loadlocks）組成。帶單只機械手的叫單臂組合設備，帶雙只機械手的叫雙臂組合設備，如圖1 所示。當組合設備運行時，機械手將待加工的晶圓從真空鎖卸載下來，按照已知的加工工藝依次送到一個或多個加工模塊，最后將完成所有加工工序的晶圓送回真空鎖中[6]。由于組合設備有兩個真空鎖，當一個真空鎖中的一批晶圓加工完后，系統開始加工另一個真空鎖中的晶圓，這樣真空鎖可以連續不斷地向系統載入晶圓，使得系統絕大多數情況下處于穩定的運行狀態。

圖1 具有雙臂機械手的組合設備示意圖

為了調度組合設備，許多學者已經在對系統建模與系統執行過程評估方面做了大量的工作[7-9]。文獻[10]指出，交換策略可以有效的簡化機械手的任務，從而減小系統的生產周期。

但在實際生產中，晶圓加工過程經常需要重入加工，例如原子層沉積工藝（atomic layer deposition，ALD）。文獻[11]指出，晶圓需要在某些加工步驟中加工多次，這使得晶圓需要多次由該加工步驟加工。文獻[12]給出了尋找最優調度的一個算法，此算法由解析表達式組成，因此非常有效。對于具有重入加工工藝的雙臂組合設備，文獻[13]提出了3-晶圓周期性調度方法。為了改善系統的運行過程及降低生產周期，文獻[14]提出了2-晶圓周期性調度方法，并證明在一些條件下2-晶圓周期性調度方法優于3-晶圓周期性調度。

然而，文獻[13]假設在局部循環中，最后一步是局部循環的瓶頸工序，并沒有指出當其他加工模塊是瓶頸工序時系統的生產周期是多少。同時文獻[14]也沒有給出當不能比較2-晶圓周期性調度方法與3-晶圓周期性調度方法時的調度系統優劣性。基于以上疑問，本文基于3-晶圓周期性調度方法，分析了一般情形下具有重入加工工藝的雙臂組合設備的生產周期，并通過仿真的方法判斷在任何條件下2-晶圓周期性調度方法與3-晶圓周期性調度方法的優劣。這對實際的生產系統是非常有意義的。

1 3-晶圓周期調度方法

為了調度具有重入加工工藝的雙臂組合設備，首先需要描述機械手的動作。其發生的事件描述如下。用mij表示機械手從PMi移動到PMj。用mLi表示機械手從真空鎖移動到PMi。用miL表示機械手從PMi移動到真空鎖。符號l表示機械手的載入動作。符號unl 表示機械手的卸載動作。si表示機械手在PMi處做一次交換（Swap，即卸載→旋轉→載入）。這些符號總結在表1 中。除此之外，還需要描述系統的動態運行過程。這樣，令Γi={Wd（q）}，i?N3表示在加工模塊PMi中的晶圓，Wd（q）表示了第d 個晶圓正在加工第q 道工序。Γ4={Wd（q）}表示了第d 個晶圓在機械手上準備加工第q 道工序。這樣，可以用M={Γ1，Γ2，Γ3，Γ4}表示系統的狀態。例如M={W3（1），W2（2），W1（3），W4（1）}表示第一、二和三枚晶圓分別在加工模塊PM3、PM2和PM1中加工其第3道、第2道和第1道工序。同時，第4枚晶圓在機械手上準備加工第一道工序。由于第一道工序必須在加工模塊PM1中進行，意味著機械手在加工模塊PM1旁等待。由此，可以通過狀態的變化描述系統的動態特性。

不失一般性，假設系統的穩態周期性調度從狀態M1={W3（1），W2（2），W1（3），W4（1）}開 始，然后系統的狀態如下：M1→M2={W4（1），W3（2），W1（3），W2（3）}→M3={W4（1），W1（4），W2（3），W3（3）}→M4={W4（1），W2（4），W3（3），W1（5）}→M5={W4（1），W3（4），W1（5），W2（5）}→M6={W4（1），W3（4），W2（5），W5（1）}→M7={W5（1），W4（2），W3（5），W6（1）}→M8={W6（1），W5（2），W4（3），W7（1）}→M9={W7（1），W6（2），W4（3），W5（3）}。可以看到，狀態M1和M8是等同的，因此，通過M1到M8形成一個周期。對于上述系統動態運行，從M1到M2、M8到M9，機械手執行順序為σ1={s1→m12→s2→m23}。從M2到M3，σ2={s3→m32→s2→m23}。從M3到M4、M4到M5重復執行σ2。σ2形成一個循環叫做局部循環。σ3={s3→m3L→l→unl→mL1}使得M5到達M6。σ4={s1→m12→s2→m23→s3→m3L→mL1}使得M6到達M7、M7到達M8。σ4形成以一個循環叫做全局循環。σ1與σ3之疊加和σ4相同。因此，從M2至M9有三個局部循環和三個全局循環，構成一個周期。在這個周期中，三個晶圓完成。因此，這是一個叫作3-晶圓周期性調度方法。同時每個機械手的動作所花費的時間見表1。

表1 系統活動的時間表示

引理3.1：基于3-晶圓調度策略的帶重入加工工藝的雙臂組合設備，如果Π1≤3Πlocal+ψ1ψ1>Π1，并且ψ1>ΠL，那么系統的生產周期為

引理3.2：基于3-晶圓調度策略的帶重入加工工藝的雙臂組合設備，如果Π1≤3Πlocal+ψ1ψ1≤Π1，并且ψ1>ΠL，那么系統的生產周期為

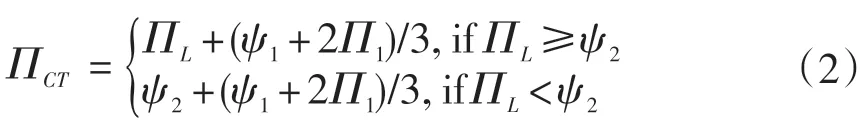
引理3.3：基于3-晶圓調度策略的帶重入加工工藝的雙臂組合設備，如果Π1≤3Πlocal+ψ1，Π1≥ΠL，ΠL≥ψ1，χ=Π1-ΠL，那么系統的生產周期為

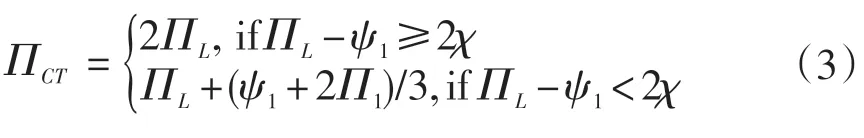
2 2-晶圓周期調度方法

當ΠL-ψ1＜2χ，3-晶圓的調度方法可能不是最優調度[13]。因此，文獻[14]提出了2-晶圓的周期性調度方法以縮短系統的生產周期。由于在條件Π3>Π2與Π3＜Π2下，2-晶圓調度策略有明顯的不同，所以分為Π3>Π2與Π3＜Π2兩種情況來討論。

調度1：假設Π3>Π2且A3≥A2+2μ+α+β，在此條件下運用2-晶圓調度方法，系統的狀態變化過程如下：M1=（{W4（1）}，{W3（2）}，{W2（5）}，{W5（1）}）→M2=（{W5（1）}，{W4（2）}，{W3（3）}，{}）→M3=（{W5（1）}，{W4（4）}，{W3（5）}，{}）→M4=（{W5（1）}，{W4（4）}，{W3（5）}，{W6（1）}）→M5=（{W6（1）}，{W5（4）}，{W4（5）}，{W7（1）}）→M6=（{W7（1）}，{W6（2）}，{W5（3）}，{}）.“{}”表示機械手為空。可以看到，狀態M1和M5是等同的。這樣M1到M5形成一個周期。對于上述系統動態運行，從M1到M2，機械手的運行順序σ1={s1→m12→s2→m23→s3→m3L→l}，此過程花費的時間為3λ+3μ+β 。從M2到M3，σ2={mL2→unl→m23→s3→m32→l→waiting at PM2→unl→m23→s3→m32→l}，這個過程形成了兩個局部循環。σ3={m2L→unl→mL1}使得M3到達M4，花費的時間為2μ+α 。σ4={s1→m12→s2→m23→s3→m3L→l→unl→mL1}使得標識從M4到達M5。σ5={s1→m12→s2→m23→s3→m3L→l}使得M5到達M6，時間花費與σ1一樣。注意到σ3和σ5組成了一個全局循環。因此σ3，σ4，和σ5組成了兩個全局循環。所以可以得到從σ2到σ5包含2 個局部循環和2 個全局循環，并且有兩個晶圓加工完成，稱這種調度方法為2-wafer調度方法。

調度2：假設Π2>Π3且A2≥A3+2μ+α+β ，此時系統演變過程如下：M7=（{W4（1）}，{W3（2）}，{W2（5）}，{W5（1）}）→M8=（{W5（1）}，{W4（2）}，{W3（3）}，{}）→M9=（{W5（1）}，{W4（4）}，{W3（5）}，{}）→M10=（{W5（1）}，{W4（4）}，{W3（5）}，{W6（1）}）→M11=（{W6（1）}，{W5（4）}，{W4（5）}，{W7（1）}）→M12=（{W7（1）}，{W6（2）}，{W5（3）}，{}）。從系統的狀態變化過程可以看到，標識M1和M5是等同的。這樣從M1到M5形成一個周期。對于上述系統動態運行，從M7到M8，σ7=σ1。從M8到M9，σ2={mL3→unl→m32→s2→m23→l→waiting at PM3→unl→m32→s2→m23→l}，這個過程形成了兩個局部循環。σ9=σ3使得M9到達M10。σ10=σ4使得M10到達M11。σ11=σ1使得M11到達M12。注意到調度2與調度1的區別在于σ2和σ8。和調度1 類似，σ9和σ10組成了一個全局循環。σ9，σ10和σ11組成了兩個全局循環。所以可以得到從σ8到σ11包含2 個局部循環和2 個全局循環，并且也有兩個晶圓加工完成。

類似于3-晶圓調度方法，兩個局部循環所花 的時間為Πlocal，這樣很明顯，當Π1≤2Πlocal+ψ1+μ 時，晶圓W6（1）在標識M4（調度1），或者在標識M10（調度2）中可不需任何等待時間就可以被機械手載入到加工模塊PM1中。而在實際生產中，條件Π1≤2Πlocal+ψ1+μ 總是滿足的。

當Π3>Π2而 A3＜A2+2μ+α+β或者，當Π2>Π3而A2＜A3+2μ+α+β 時，根據文獻[6]的研究成果此時并不能判斷3-晶圓與2-晶圓哪種調度方法更好。這樣開發了仿真算法可有效的計算出2-晶圓調度方法下，系統的生產節拍。這樣通過與3-晶圓調度方法下，系統的生產節拍相比較，可判斷哪種調度方法更優。

令Ti表示仿真時間鐘，初始時刻為T0=0。基于盡早加工策略，有對具有重入加工工藝的雙臂組合設備的仿真程序如下。

調度算法1：當Π3>Π2，基于調度1，系統的仿真算法如下：

1）T1=μ+β；m12→l（機械手將晶圓W1（2）載入到PM2）

2）T2=μ+α+μ；m2L→unl→mL1

3）T3=max{A1–（T1+T2），0}；在PM1處等待

4）T4=λ；s1（機械手在PM1處做一次交換并將晶圓W3（1）載入到PM1）

5）T5=μ；m12

6）T6=max{A2–（T2+T3+T4+T5），0}；在PM2處等待

7）T7=λ；s2（機械手在PM2處做一次交換并將晶圓W2（2）載入到PM2）

8）T8=μ+β；m23→l（機械手將晶圓W1（3）載入到PM3），此時系統的狀態（{W3（1）}，{W2（2）}，{W1（3）}，{}）

9）T9=μ；m32

10）T10=max{A2–（T8+T9），0}；在PM2處等待

11）T11=α+μ；unl→m23

12）T12=max{A3–（T9+T10+T11），0}；在PM3處等待

13）i=0

14）While i≤5

15）T13+i=λ；s3（機械手在PM3處做一次交換并將晶圓W2（3）載入到PM3）

16）T14+i=μ+β；l（機械手將晶圓W1（4）載入到PM2）

17）T15+i=A2；在PM2處等待

18）T16+i=α+μ；unl→m23

19）T17+i=max{A3-（T14+i+T15+i+T16+i），0}；在PM3處等待

20）T18+i=λ；s3（機械手在PM3處做一次交換并將晶圓W1（5）載入到PM3）

21）T19+i=μ+β；l{W2（4）}——此時系統的狀態（{W3（1）}，{W2（4）}，{W1（5）}，{}）

22）T20+i=μ+α+μ+λ；m2L→unl→mL1→s1（機械手在PM1處做一次交換并將晶圓W4（1）載入到PM1）

23）T21+i=μ；m12

24）T22+i=max{A2-（T20+i+T21+i），0}；在PM2處等待

25）T23+i=λ；s2（機械手在PM2處做一次交換并將晶圓W3（2）載入到PM2）

26）T24+i=μ；m23

27）T25+i=max{A3-（T19+i+T20+i+T21+i+T22+i+T23+i+T24+i），0}；在PM3處等待

28）T26+i=λ；s3（機械手在PM3處做一次交換并將晶圓W2（5）載入到PM3）

29）T27+i=μ+β+α+μ；m3L→l→unl→mL1

30）T28+i=max{A1-（T21+i+T22+i+T23+i+T24+i+T25+i+T26+i+T27+i），0}；在PM1處等待

31）T29+i=λ；s1（機械手在PM1處做一次交換并將晶圓W5（1）載入到PM1）

32）T30+i=μ；m12

33）T31+i=max{A2-（T24+i+T25+i+T26+i+T27+i+T28+i+T29+i+T30+i），0}；在PM2處等待

34）T32+i=λ；s2（機械手在PM2處做一次交換并將晶圓W4（2）載入到PM2）

35）T33+i=μ；m23

36）T34+i=max{A3-（T27+i+T28+i+T29+i+T30+i+T31+i+T32+i+T33+i），0}；在PM3處等待

37）T35+i=λ；（機械手在PM2處做一次交換并將晶圓W3（3）載入到PM3）

38）T36+i=μ+β；m3L→l——此時系統的狀態（{W5（1）}，{W4（2）}，{W3（3）}，{}）

39）T37+i=μ；mL2

40）T38+i=max{A2-（T33+i+T34+i+T35+i+T36+i+T37+i），0}；在PM2處等待

41）T37+i=α+μ；unl→m23

42）T40+i=max{A3-（T36+i+T37+i+T38+i+T39+i），0}；在PM3處等待

43）i=i+1；

調度算法2：當Π2>Π3，基于調度2，系統的仿真算法如下：

1）T1=μ+β；m12→l（機械手將晶圓W1（2）載入到PM2）

2）T2=μ+α+μ；m2L→unl→mL1

3）T3=max{A1-（T1+T2），0；在PM1處等待

4）T4=λ；s1（機械手在PM1處做一次交換并將晶圓W3（1）載入到PM1）

5）T5=μ；m12

6）T6=max{A2-（T2+T3+T4+T5），0}；在PM2處等待

7）T7=λ；s2（機械手在PM2處做一次交換并將晶圓W2（2）載入到PM2）

8）T8=μ+β；m23→l（機械手將晶圓W1（3）載入到PM3），此時系統的狀態（{W3（1）}，{W2（2）}，{W1（3）}，{}）

9）T9=A3；在PM3處等待

10）T10=α+μ；unl→m32

11）T11=max{A2-（T8+T9+T10），0}；在PM2處等待

12）i=0

13）While i≤5

14）T12+i=λ；s2（機械手在PM2處做一次交換并將晶圓W1（4）載入到PM2）

15）T13+i=μ+β；m23→l{W2（3）}

16）T14+i=A3；在PM3處等待

17）T15+i=α+μ；unl→m32

18）T16+i=max{A2-（T13+i+T14+i+T15+i），0}；在PM2處等待

19）T17+i=λ；s2（機械手在PM2處做一次交換并將晶圓W2（4）載入到PM2）

20）T18+i=μ+β；m23→l{W1（5）}——此時系統的狀態（{W3（1）}，{W2（4）}，{W1（5）}，{}）

21）T19+i=μ+α+μ+λ；m3L→unl→mL1→s1（機械手在PM1處做一次交換并將晶圓W4（1）載入到PM1）

22）T20+i=μ；m12

23）T21+i=max{A2-（T18+i+T19+i+T20+i），0}；在PM2處等待

24）T22+i=λ；s2（機械手在PM2處做一次交換并將晶圓W3（2）載入到PM2）

25）T23+i=μ；m23

26）T24+i=max{A3-（T19+i+T20+i+T21+i+T22+i+T23+i），0}；在PM3處等待

27）T25+i=λ；s3（機械手在PM3處做一次交換并將晶圓W2（5）載入到PM3）

28）T26+i=μ+β+α+μ；m3L→l→unl→mL1

29）T27+i=max{A1-（T20+i+T21+i+T22+i+T23+i+T24+i+T25+i+T26+i），0}；在PM1處等待

30）T28+i=λ；s1（機械手在PM1處做一次交換并將晶圓W5（1）載入到PM1）

31）T29+i=μ；m12

32）T30+i=max{A2-（T23+i+T24+i+T25+i+T26+i+T27+i+T28+i+T29+i），0}；在PM2處等待

33）T31+i=λ；s2（機械手在PM2處做一次交換并將晶圓W4（2）載入到PM2）

34）T32+i=μ；m23

35）T33+i=max{A3–（T26+i+T27+i+T28+i+T29+i+T30+i+T31+i+T32+i），0}；在PM3處等待

36）T34+i=λ；s3（機械手在PM3處做一次交換并將晶圓W3（3）載入到PM3）

37）T35+i=μ+β；m3L→l——此時系統的狀態（{W5（1）}，{W4（2）}，{W3（3）}，{}）

38）T36+i=μ；mL3

39）T37+i=max{A3-（T35+i+T36+i），0}；在PM3處等待

40）T38+i=α+μ；unl→m32

41）T39+i=max{A2-（T32+i+T33+i+T34+i+T35+i+T36+i+T37+i+T38+i），0}；在PM2處等待

42）i=i+1；

3 實例分析

實例1：假設工序1加工時間A1為90 s，工序2 的加工時間A2為50 s，工序3 加工時間A3為60 s。另外機械手的卸載時間、裝載時間和移動時間相等，且α=β=μ=5 s 。機械手執行交換的時間為13 s，即λ=13 s 。

由以上工藝參數可知Π3=73 s>Π2=63 s ，那么選擇2-晶圓調度中的調度算法1 進行調度該系統。可得系統的生產節拍為ΠCT=（166+1/2）s 。如果采用3-晶圓調度策略，基于引理3.3 可以得到系統的生產周期為ΠCT=（164+2/3）s 可知3-晶圓調度策略要比2-晶圓調度策略在此條件下優越。

實例2：假設工序1加工時間A1為90 s，工序2 的加工時間A2為80 s，工序3 加工時間A3為70 s。另外機械手的卸載時間、裝載時間和移動時間相等，且α=β=μ=5 s 。機械手執行交換的時間為13 s，即λ=13 s 。

由以上工藝參數可知Π2=93>Π3=83，那么選擇2-晶圓調度中的調度算法2 進行調度該系統，可得系統的生產節拍為ΠCT=200 s 。如果采用3-晶圓調度策略，基于引理3.3 可得到系統周期為ΠCT=186 s 。可知在此條件下3-晶圓調度策略要比2-晶圓優越。

4 結束語

本文對3-晶圓調度策略和2-晶圓調度策略進行了詳細闡述，并給出了在全部條件下運用3-晶圓策略調度系統時系統的生產周期計算節拍。對于采用2-晶圓調度方法調度帶重入加工工藝的雙臂組合設備時，給出了計算系統生產周期的調度算法，此算法由解析表達式組合，因此執行過程非常有效。通過比較兩種調度策略下系統的生產節拍，可有效的判斷哪一種方法更適合該系統。今后將重點研究在包含以上約束條件下，同時考慮帶駐留時間約束的雙臂組合設備。

［1］M.Bader，R.Hall，G.Strasser.integrated processing equipment ［J］.Solid State Technol.，1990，33：149-154.

［2］P.Burggraaf.Coping with the high cost of wafer fabs［J］.Smicond.Int.，1995，38：45-50.

［3］B.Newboe.Cluster tools：a process solution［J］.Semiconductor Int.，1990，13（8）：82-88.

［4］T.K.McNab.Cluster tools，part 1：emerging processes［J］.Semiconductor Int.，vol.13（9）：58-63.

［5］P.Singer.The driving forces in cluster tool development［J］.Semiconductor Int.，1995，18（8）：113-118.

［6］N.Q.Wu，C.B.Chu，F.Chu，et al.A Petri net method for schedulability and scheduling problems in single-arm cluster tools with wafer residency time constraints［J］.IEEE Transactions on Semiconductor Manufacturing，2008，21（2）：224-237.

［7］J.Yi，S.Ding，M.Zhang.Steady-state throughput and scheduling analysis of multi-cluster tools：A decomposition approach［J］.IEEE Trans.Automation Sci.Eng。，Apr.2008，5（2）：321-336.

［8］W.M.Zuberek.Timed Petri nets in modeling and analysis of cluster tools［J］.IEEE Trans.Robot.Automat.，Oct.2001，17（5）：562-575.

［9］N.Q.Wu，M.C.Zhou.Colored timed Petri nets for modeling and analysis of cluster tools［J］.Asian Journal of Control，2010，12（3）：253-266.

［10］S.Venkatesh，R.Davenport，P.Foxhoven，et al.A steady state throughput analysis of cluster tools：Dual-blade versus single-blade robots［J］.IEEE Trans.Semicond.Manuf.，1997，10：418-424.

［11］H.-Y.Lee，T.-E.Lee.Scheduling single-arm cluster tools with reentrant wafer flows ［J］.IEEE transactions on Semiconductor Manufacturing，2006，19（2）：226-240.

［12］N.Q.Wu，F.Chu，C.B.Chu，et al.Petri net-based scheduling of single-arm cluster tools with reentrant atomic layer deposition processes［J］.IEEE Transactions on Automation Science and Engineering，2011，8（1）：42-55.

［13］N.Q.Wu，F.Chu，C.B.Chu，et al.Zhou.Petri net modeling and cycle-time analysis of dual-arm cluster tools with wafer revisiting ［J］.IEEE Transactions on Systems，Man，and Cybernetics：Systems，Jan.2013，43（1）：

［14］N.Q.Wu，M.C.Zhou.A novel scheduling approach to dual-arm cluster tools with wafer revisiting［A］.IEEE International Conference on Systems，Man，and Cybernetics［C］.2012.