基于網格變形技術的全附體潛艇操縱性計算＊

孫銘澤 王永生 張志宏 戴余良

（海軍工程大學船舶與動力學院 武漢 430033）

0 引 言

潛艇水動力系數的數值計算主要是基于勢流理論.隨著計算流體力學和計算機技術的飛速發展，目前基于雷諾時均方法（RANS）的數值模擬成為操縱性試驗數值計算的熱點.潛艇操縱性物理試驗主要有直線拖曳試驗（ORT）、回轉臂試驗（RAT）以及平面運動機構試驗（PMM）.以往操縱性的數值模擬主要集中于前2種試驗.文獻［1］系統闡述了基于粘性流的CFD方法在潛體操縱性預報中的重要作用，并以SUBOFF幾何為研究對象，計算了在不同攻角下的流場，并將不同湍流模型下的計算結果與試驗數據以及基于遲滯分離渦（DDES）模型的計算結果進行了比較；文獻［2］從網格第一層節點距離、網格數量以及湍流模型等方面論述了操縱性計算的數值方法，并與試驗數據進行了對比，該文獻認為，第一層網格節點距離的取值應使無因次距離y＋介于40～100之間，而縱向力的精確預報相對于側向力或力矩需要較多的網格數量，同時指出了大漂角姿態下的操縱性精確預報的缺陷；文獻［3］應用CFD 軟件對潛艇的直線拖曳試驗和回轉臂試驗進行了大量的數值計算，得到了在線性或弱非線性前提下的粘性類水動力系數和舵角系數；文獻［4］采用6 種不同的湍流模式計算了SUBOFF 2種模型在變漂角和變攻角條件下的操縱性水動力，并與試驗值進行比較，計算誤差在20%以內，該文獻認為κ－ω SST 模型較為適合進行潛艇操縱性數值計算.以上所述的潛艇操縱性數值計算只能獲取潛艇粘性類水動力系數，而不能計算慣性類水動力系數，所需要進行的計算量較為龐大，限制了潛艇操縱性的快速預報.而PMM 數值試驗卻能較好地解決這個問題.

文獻［5－6］系統地闡述了利用基于動網格技術的FLUENT 軟件實現平面運動的方法，該方法通過編寫UDF函數控制四面體網格節點位移來實現網格運動，并在運動中求解瞬態雷諾時均方程從而對操縱性進行快速預報.由于結構化網格較非結構化網格在網格正交性、計算收斂性以及對數值耗散的抑制等方面具有優勢，基于結構化網格的數值計算結果將更為可信，于是利用六面體網格進行PMM 試驗的數值模擬勢必成為主流，然而這方面的發展較少見于報道.

本文以有精細試驗數據的DARPA－2全附體SUBOFF潛艇為分析對象，以全局映射式六面體網格進行空間離散，利用基于網格變形技術的ANSYS CFX 軟件，實現了潛艇小振幅PMM 試驗的虛擬仿真，同時也進行了直線拖曳試驗和回轉臂試驗的數值計算，并將計算結果與試驗數據進行對比，闡述了該方法在操縱性計算領域的適用性，證明了該方法在計算水動力系數時的可靠性，提供了潛艇操縱性快速預報的一種新途徑.

1 基本理論與控制方程

1.1 控制方程

目前廣泛使用雷諾時均法來考察瞬時值的影響，用張量的形式表述不可壓湍流作時間平均處理的控制方程為

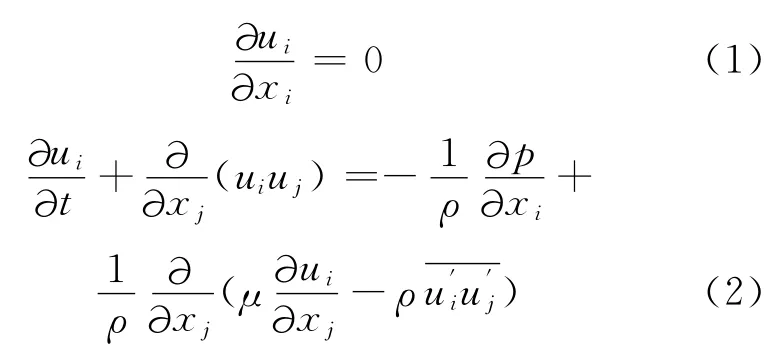
1.2 網格變形方程

CFX 軟件所提供的網格變形技術［7］能夠使指定的邊界或子域內的節點按照CEL 語句所規定的規律進行變形，這項技術主要是在求解瞬態RANS方程之前求解位移擴散方程，該方程使邊界或子域附近的節點適應性地運動

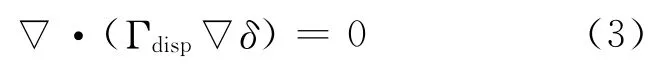
式中：δ為相對位移；（Γdisp為網格剛度系數，默認為1m2／s.

2 PMM 試驗的數值實現

潛艇PMM 試驗主要包括：純升沉運動、純俯仰運動、純橫蕩運動和純搖艏運動.利用CFX 軟件實現各種運動，通過編寫CEL語句控制節點位移，同時控制體進口方向模擬無限遠來流，設來流速度為v＝3.05m／s.

2.1 數值計算的準備

計算時為了保證網格變形的質量，將潛艇壁面附近一定范圍內的流場單獨設置為子域（subdomain），外部流場與子域通過設置交界面進行數據傳遞，整個流場邊界范圍為：來流方向取1 L，下游方向取2 L，徑向取1 L，L 為潛艇全長，見圖1.

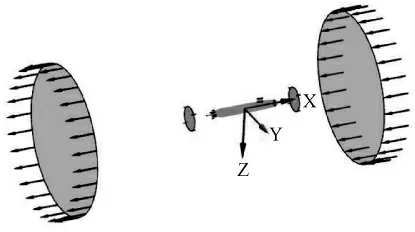
圖1 計算域的設置

本文的計算案例中計算域均采用全局映射式六面體網格進行離散，這部分工作在專業網格劃分軟件ICEM CFD 中完成，見圖2.為了適應所采用的SST 湍流模型的需要，需控制網格壁面第一層距離.同時，為了適應潛艇不同姿態下的分離流動，在翼面及主艇體背流區域的網格進行局部加密.另一方面，將潛艇艇體附近的網格與遠離艇體部分的流場分離開來，并使該子域內的所有網格節點按指定規律同步運動以保證網格質量，見圖3.網格節點總數約為156萬.

圖2 艇體表面網格

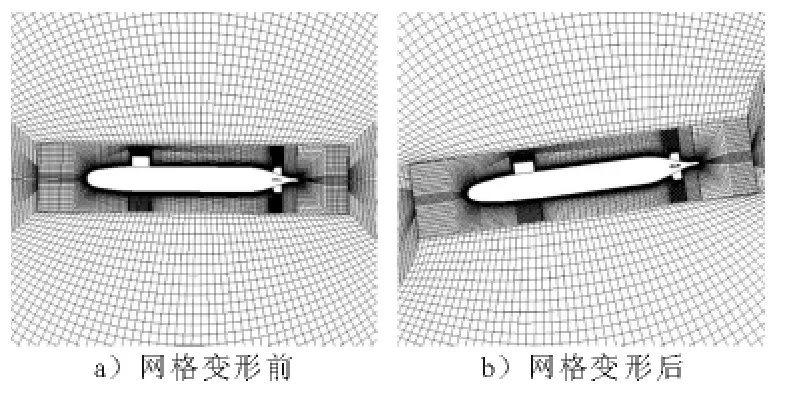
圖3 縱中剖面網格變形前后比較（純俯仰運動）

2.2 操縱性計算

2.2.1 速度與加速度系數的求取 基于線性理論的小振幅平面運動機構主要是為了測定線性水動力系數，而純升沉運動和純橫蕩運動是為了求取速度與加速度系數，以純升沉運動為例，由水動力系數的意義可得線性方程

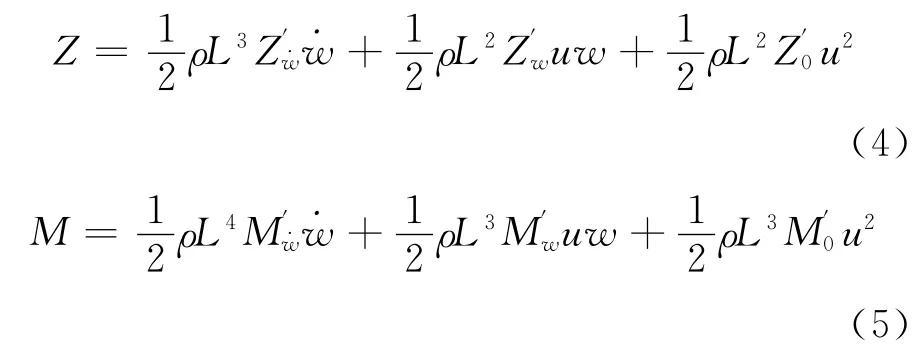
設定振幅a＝300mm，艇長L＝4.356m，模型的運動規律為

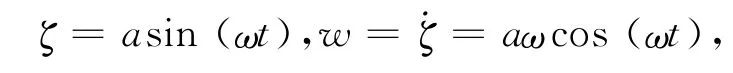
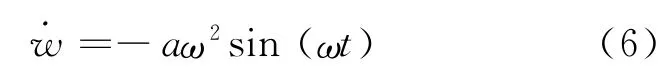
式中：ζ為潛艇的垂向位移；ω 為周期運動圓頻率，ω＝2πf；f 為運動頻率，為了使迭代時間步長取整數，將頻率設置為：0.2，0.25，0.3125，0.4，0.5，0.625Hz；w 和˙w 分別為垂向運動速度和加速度.

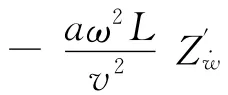
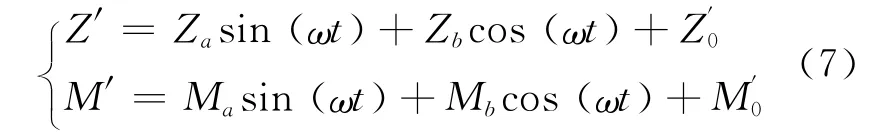
計算時使子域內的網格節點按正弦規律作小幅振動，將一個運動周期分為40個時間步，通常計算6個周期便可得到穩定的垂向力和俯仰力矩關于時間的變化曲線，見圖4.

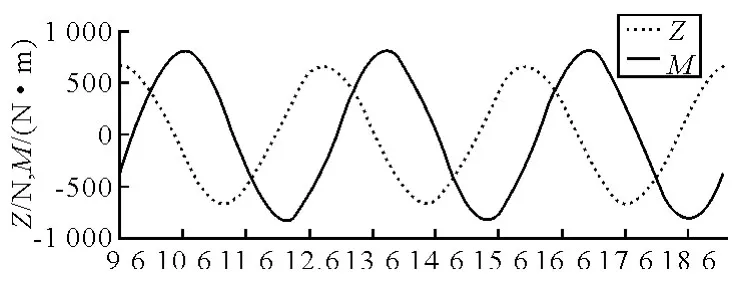
圖4 純升沉運動垂向力Z 和俯仰力矩M 的迭代曲線（f＝0.3125Hz）

文獻［8］對物理試驗的數據處理方法做了闡述，依照分量分離的方法，將水動力的同相分量與正交分量分開.可以采用Fourier級數展開到1階的方法進行分量分離，計算曲線見圖5，由該曲線擬合出的速度系數和加速度系數為

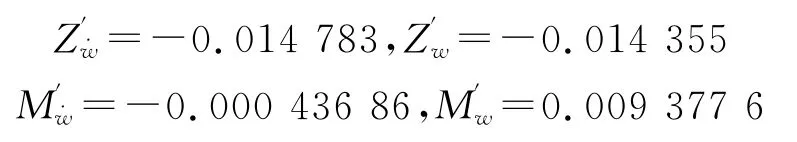
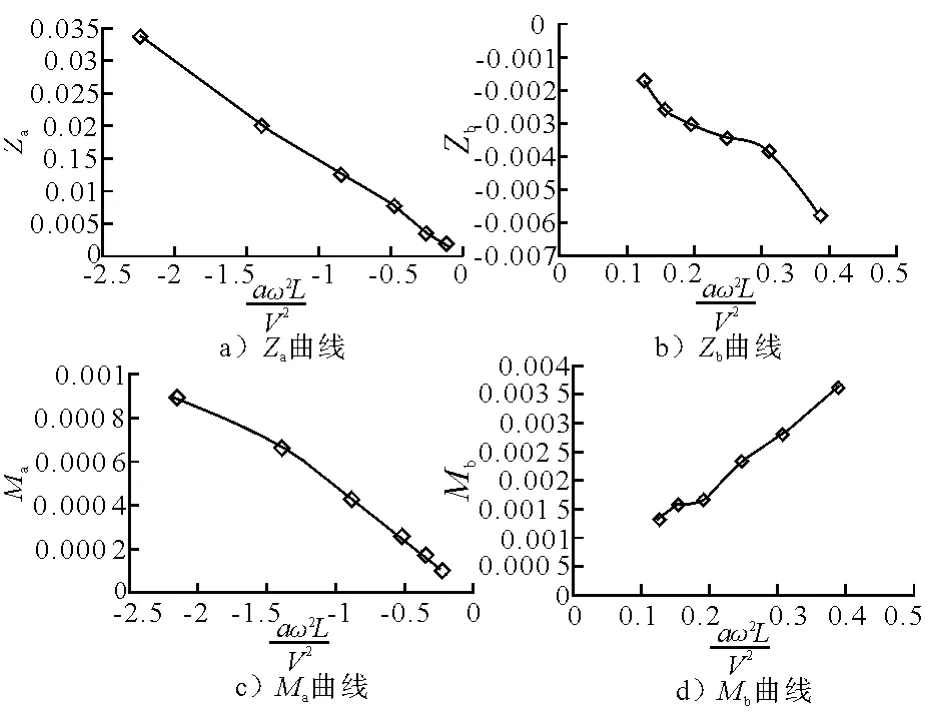
圖5 純升沉運動水動力系數求取曲線

純橫蕩運動與純升沉運動非常相似，將潛艇模型置于橫臥狀態進行運動即可.在此直接給出水動力系數計算結果，見圖6，據此擬合出的關于側向速度v的速度系數和加速度系數為

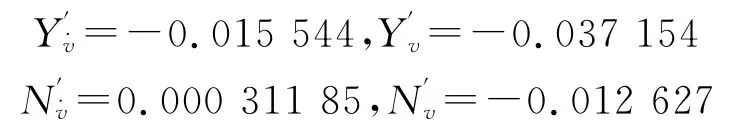
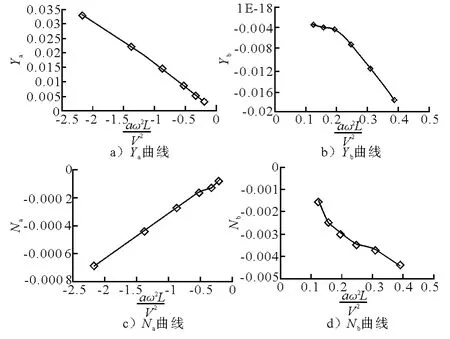
圖6 純橫蕩運動水動力系數求取曲線

2.2.2 角速度和角加速度系數的求取 純俯仰運動和純搖艏運動則是為了求取角速度和角加速度系數.同上述分析，在小振幅運動的線性前提下可寫出純俯仰運動的水動力方程

設定純俯仰運動的振幅θ0＝π／30rad，則純俯仰運動的運動方程為

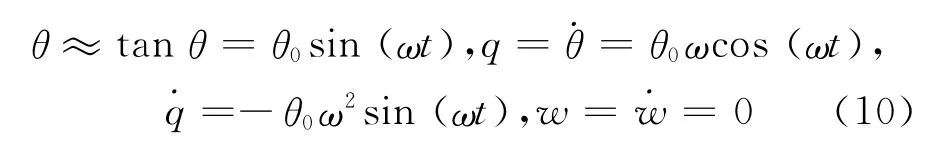
式中：θ為潛艇模型的縱傾角.

數值試驗中，通過編寫CEL 語句，一方面使子域內的節點按正弦規律上下振動，另一方面則繞重心在垂直面內按正弦規律轉動，那么兩種運動的合成就是純俯仰運動.計算時與純升沉運動一樣，將一個周期分為40個時間步，計算6～8個周期就可以得到穩定的垂向力和俯仰力矩關于時間的變化曲線，對該曲線按Fourier級數展開至1階，取不同頻率下的1階系數擬合出相應的角速度和角加速度系數，圖表數據略，直接給出計算得到的水動力系數如下

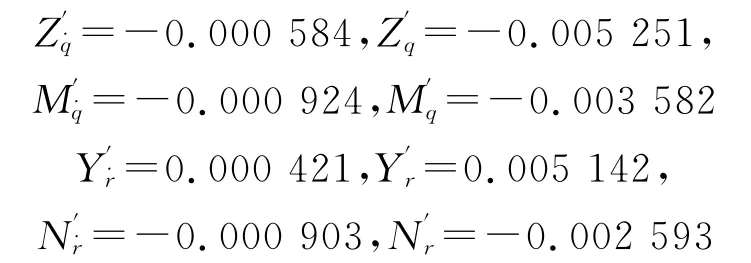
2.3 計算結果校驗與分析

美國泰勒研究中心做了SUBOFF 全附體潛艇（AFF－8幾何）的操縱性試驗，并公布了部分水動力系數試驗數據［9］.將本文計算得到的水動力系數與試驗數據進行對比［10］，見表1～2.

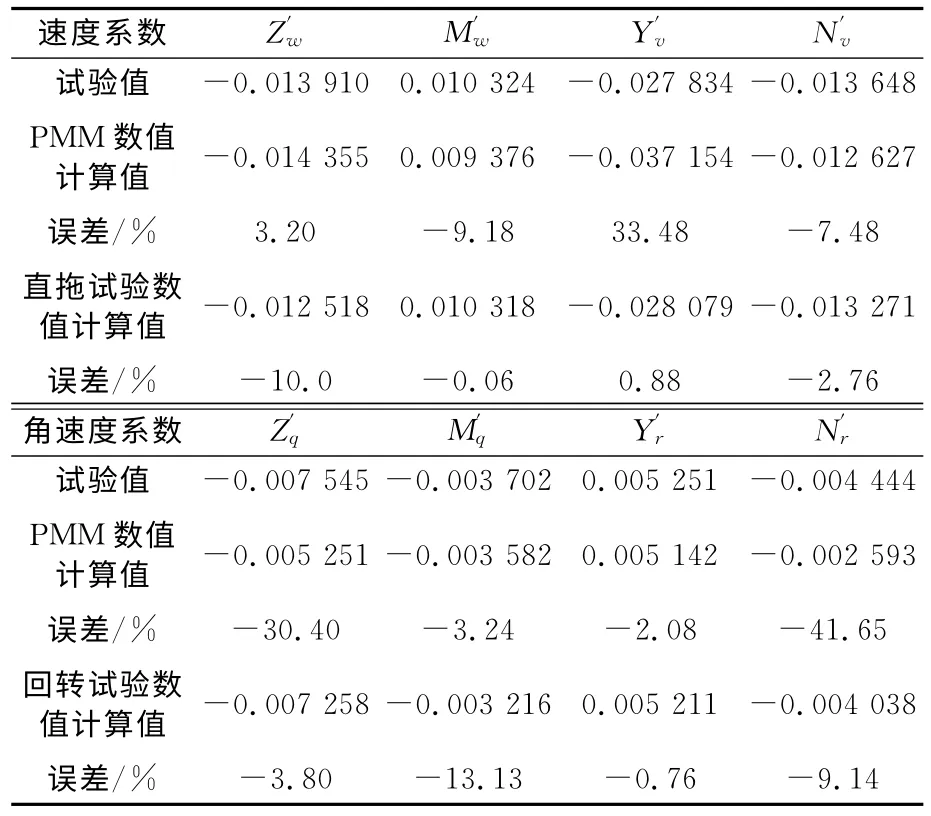
表1 粘性類水動力系數對比

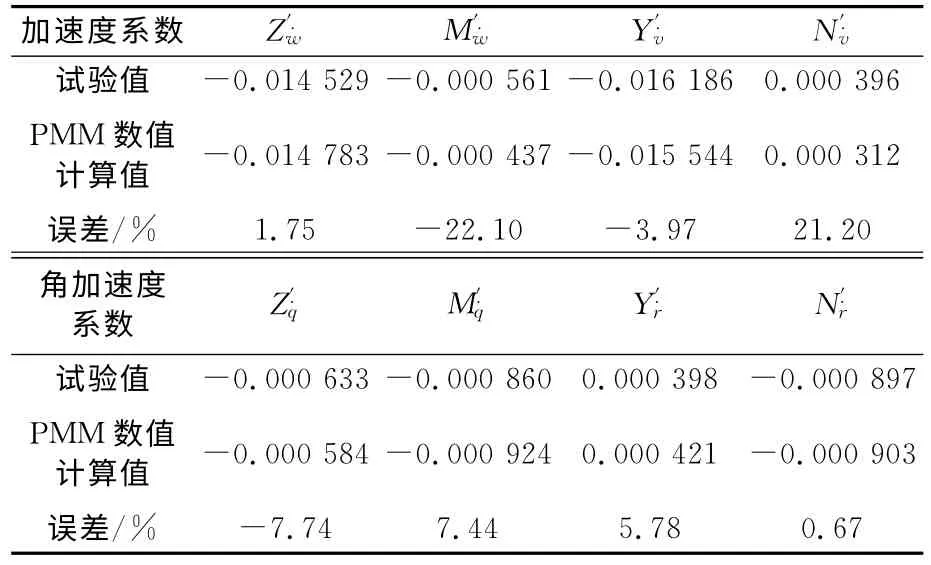
表2 慣性類水動力系數對比

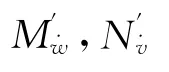
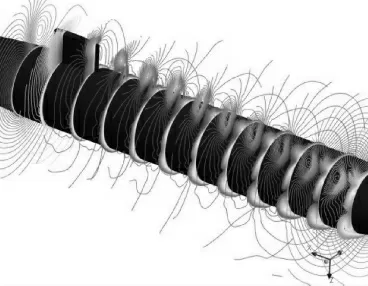
圖7 RANS模擬潛艇渦量場沿流動方向的演變（純橫蕩運動，f＝0.2Hz）

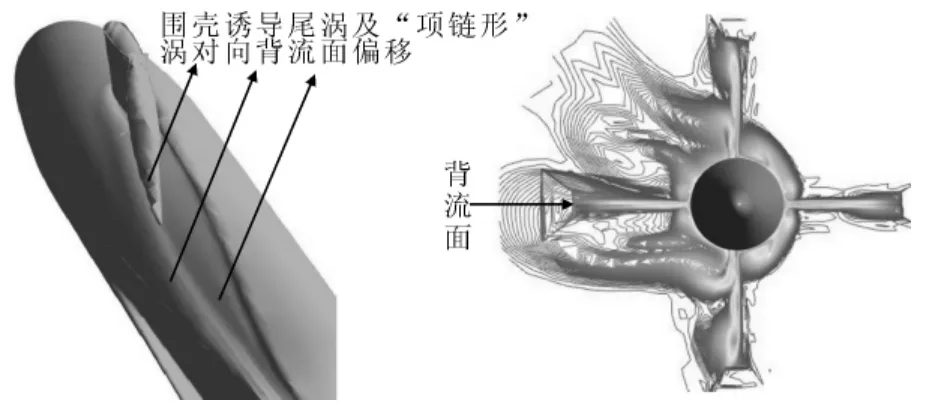
圖8 純橫蕩運動中潛艇處于平衡位置時渦量向背流面的偏移

文獻［7］指出，由純升沉和純橫蕩試驗所測出的水動力系數中，速度系數的值較小，所得之測量值往往離散度較大，所以速度系數一般仍由直拖試驗來確定.從表1中也可以看出，由PMM 數值試驗求得的速度系數與直拖試驗或回轉試驗所得結果相比誤差稍大，但精度仍稍高于文獻［6］由PMM 數值計算得到的粘性類系數的計算精度.另一方面，PMM 試驗所采用的數學模型是基于小振幅線性假設的，并沒有考慮非線性項和耦合項的影響，這也是產生誤差的重要原因之一.

從計算效率的角度來看，要想精確獲得全部速度系數，直拖數值試驗至少需要12個不同的攻角姿態以及同等數量的不同的漂角姿態，計算耗時較長，而PMM 數值試驗只需要在5～6個頻率下進行純升沉和純橫蕩試驗即可，角速度系數的計算耗時與此類似.另一方面，直拖數值試驗和回轉數值試驗不能在穩態條件下獲得慣性類水動力系數，這也限制了此二者的應用范圍.PMM 數值試驗的最大的優勢在于可在一組試驗中同時求出慣性類系數和粘性類系數，基于大振幅非線性理論的PMM 數值試驗也可獲得非線性系數和諸多耦合系數，從而減少了數值試驗次數，提高了計算效率，這對潛艇操縱性的快速預報具有重要意義.

3 結 論

1）潛艇PMM 試驗的數值計算結果與DTRC所公布的試驗數據取得較好一致，整體誤差能夠控制在8%以內，只有極少數水動力系數與試驗值偏差超過了20%，從數值模擬的整體上看計算結果是真實可信的.

2）潛艇PMM 數值模擬可以較快地獲取相關的水動力系數，且在一組計算內既能夠獲得慣性類水動力系數也能夠獲得粘性類水動力系數，這是直拖數值試驗或回轉試驗數值計算所不具有的優勢.

3）潛艇PMM 試驗的數值模擬所獲得的慣性類水動力系數具有較高的精度，而粘性類水動力系數計算精度不如直拖試驗或回轉試驗數值計算的精度高，若只要求獲得粘性類系數，本研究建議仍采用常規試驗方法.

［1］VAZ G，TOXOPEUS S，HOLMES S.Calculation of manoeuvring forces on submarines using two viscous－flow solvers［C］∥Proceedings of the ASME 201029thInternational Conference on Ocean，Offshore and Arctic Engineering，OMAE，2010.

［2］ZENG Guanghui，ZHU Jun.Study on key techniques of submarine maneuvering hydrodynamics prediction using numerical method［C］∥2010Second In－ternational Conference on Computer Modeling and Simulation，ICCMS，Taiyuan，China，Oct.21，2010.

［3］詹成勝，劉祖源，程細得.潛艇水動力系數數值計算［J］.船海工程，2008，37（3）：1－4.

［4］柏鐵朝，梁中剛，周軼美.潛艇操縱性水動力數值計算中湍流模式的比較與應用［J］.中國艦船研究，2010，5（2）：22－28.

［5］ZHANG He，YU Yuru，CAI Haopeng.Using CFD software to calculate hydrodynamic coefficients［J］.Marine.Sci，2010（9）：149－155.

［6］張曉頻，龐永杰.多功能潛水器操縱性能與運動仿真研究［D］.哈爾濱：哈爾濱工程大學，2008.

［7］王化明，鄒早建.雙槳多舵船舶操縱性預報研究［J］.武漢理工大學學報：交通科學與工程版，2006，30（1）：124－127.

［8］陳厚泰.潛艇操縱性［M］.北京：國防工業出版社，1981.

［9］RODDY R F.Investigation of the stability and control characteristics of several configurations of the darpa suboff model（DTRC model 5470）from captive－model experiments［R］.David Taylor Research Center，Ship Hydrodynamics Department，1990.

［10］ANSYS Inc.Turbulence and near－wall modeling［M］.Canonsburg：ANSTS CFX－Solver Modeling Guide，2009.