類電磁機制算法求解模糊流水車間調度問題＊

邵 揚 王曉娟

（武漢理工大學物流工程學院 武漢 430063）

0 引 言

很多調度優化問題都針對的是靜態環境下的，但是實際生產過程中，由于設備、環境和人為因素的影響，工件的加工時間、交貨期等參數通常是不確定的值.不確定環境下的流水車間調度問題（flow shop scheduling problem，FFSP）已經引起了國內外一些學者的關注，Balasubramanian和Grossmann［1］提出了一種新型的分支定界方法求解了加工時間不確定的流水車間調度問題，Nezhad和Assadi［2］提出了一種改進的CDS算法求解了模糊流水車間調度問.Javadi等［3］針對多目標無等待的流水車間調度問題提出了一種模糊多目標的線性規劃模型.Hong和Wang［4］研究了加工時間不確定的柔性流水車間調度問題.Wu［5］給予遺傳算法求解了加工時間和交貨期不確定的流水車間調度問題.類電磁機 制（electromagnetism－like mechanism，EM）算法由Birbil在2002 年提出［6］，是一種基于群體的全局優化算法，它通過模擬電磁場中的吸引－排斥機制，來實現對全局最優值的搜索.該算法已在函數優化［7］、神經網絡訓練［8］等優化問題中獲得成功應用.本文采用模糊數來表示不確定的加工時間和交貨期，通過引入隨機鍵的表達方式，采用了EM 算法對模糊流水車間調度問題進行了求解.

1 類電磁機制（EM）算法簡介

1.1 EM 算法的基本原理

類電磁機制算法是一種基于種群的優化算法，將每個解比作一個帶電粒子，每個粒子的電荷的多少由該粒子對應的目標函數值確定，而電荷的多少決定了該粒子對種群其他粒子的吸引或者排斥的強弱，目標函數值越優，吸引或排斥力就越大.然后通過吸引或排斥力確定每個粒子下一步的移動方向，使搜索粒子都向著較優解所在區域移動.

1.2 EM 算法的基本步驟

EM 算法主要由4個基本步驟組成：初始化、局部搜索、計算合力和移動粒子.下面以函數優化為例，介紹該算法的基本步驟，求目標函數f（x）在可行域中的最小值.

1.2.1 初始化 從已知可行域中隨機選取m 個點作為初始粒子，然后計算出每個粒子的目標函數值f（xi），并將目標函數值最優的粒子記為xbest，也稱其為當前最優粒子.

1.2.2 局部搜索 局部搜索主要用來在單個粒子的領域范圍內改進當前種群已搜索到的解.實驗表明，當只對當前最優粒子進行局部搜索時，能較好地維持速度和精度的平衡.

1.2.3 計算每個粒子的合力 首先根據每個粒子的目標函數值計算每個粒子所帶的電荷量，電荷的計算公式為

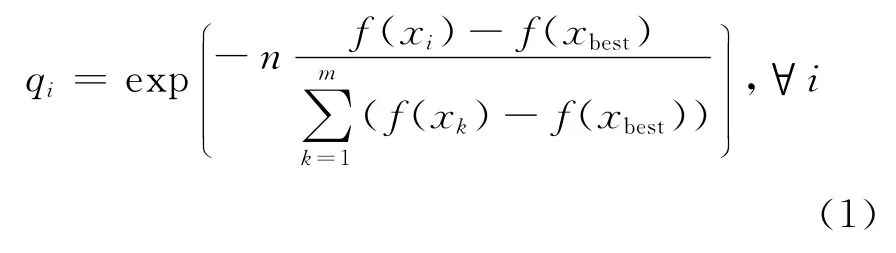
然后計算作用在粒子i上的合力Fi，根據下式計算.

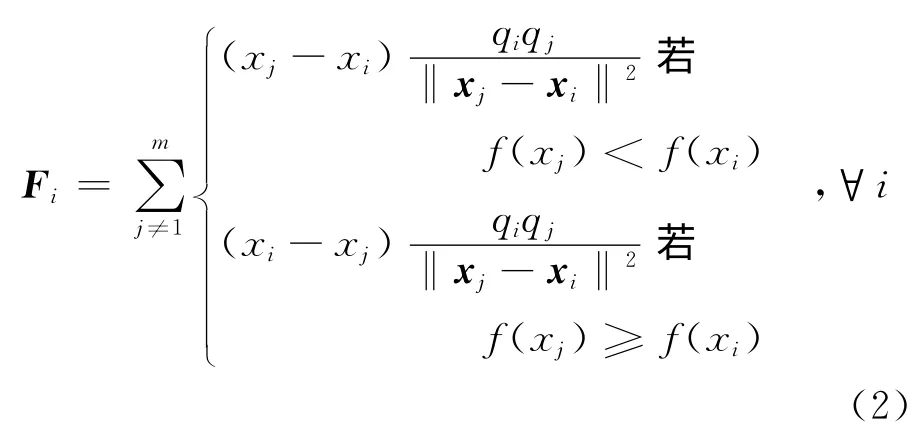
根據這個公式，目標函數值較優的粒子將擁有較大的電荷數，具有更強的吸引或者排斥力力；另外，目標函數值較優的粒子將吸引其他粒子，反之，目標函數值較差的粒子將排斥其他粒子.

1.2.4 移動粒子 粒子i將沿著合力Fi的方向移動，步長λ為一個在［0，1］上均勻分布的隨機值.在式（3）中，RNG 為一個向量，其分（向）量表示對應的朝上邊界uk或者下邊界lk移動的可行步長.粒子每一步移動為：

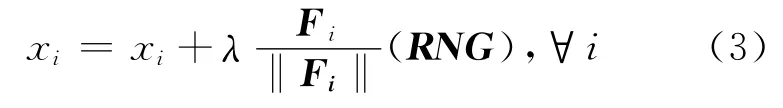
2 模糊數相關理論

2.1 模糊數和操作

本文用模糊數來表示不確定的加工時間和交貨期，用三角模糊數表示不確定的加工時間，三角模糊數如圖1所示.用梯形模糊數來表示不確定的交貨期，如圖2所示.

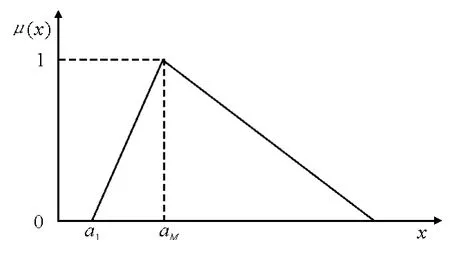
圖1 三角模糊數

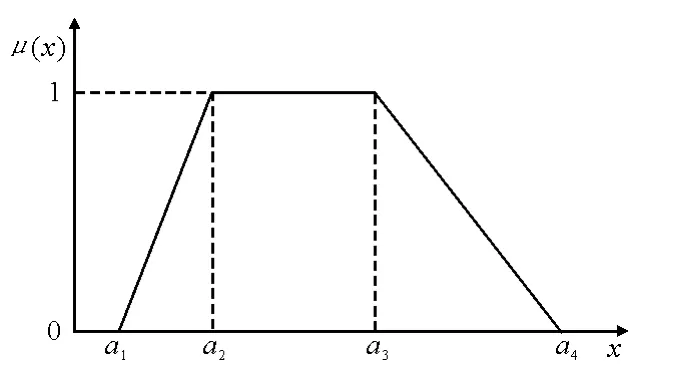
圖2 梯形模糊數

模糊調度問題中，模糊數的操作是很重要的問題，它包括模糊數的求和、取大以及模糊數的比較.

1）求和 對于三角模糊數和梯形模糊數，求和操作為

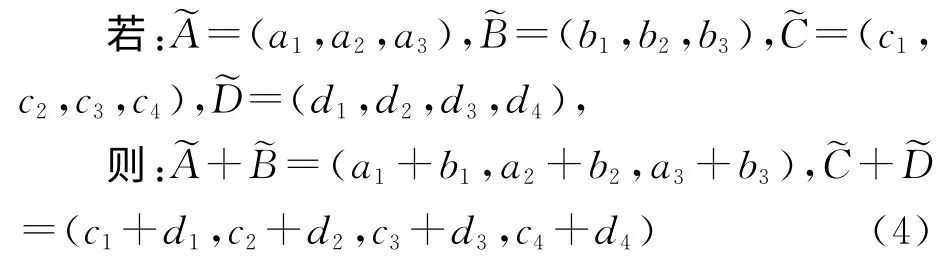
2）取大 三角模糊數的取大操作為

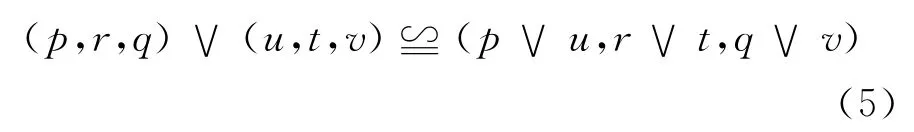
2.2 模糊數的比較

模糊數間的比較操作，采用Sakawa等人提出的準則進行［9］.

3 EM 求解模糊流水車間調度問題

3.1 優化目標

1）最大化平均滿意度

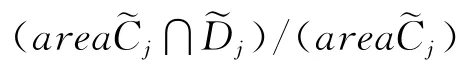
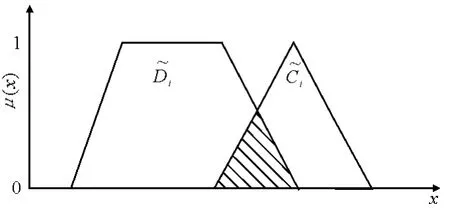
圖3 滿意度（AI）

2）最小化最大模糊完工時間

3.2 求解流程

通過引入隨機鍵的編碼方式，將離散型的工件排序編碼轉換成能用EM 算法直接求解的連續型編碼.基于EM 的模糊流水車間調度算法的步驟如下.

步驟1 將每個粒子通過隨機鍵的編碼方式映射成調度問題的一個解，初始化粒子.

步驟2 利用模糊數的求和與取大操作，計算出各粒子的目標函數值.

步驟3 進行局部搜索.

步驟4 根據式（1），（2）計算合力.

步驟5 根據式（3）計算位移，移動粒子.

步驟6 若算法達到最大迭代次數，則算法停止；否則，返回步驟2繼續迭代.

4 測試與結果比較

1）最大化平均滿意度 本文采用了文獻［10］和［11］中的測試實例，以最大化平均滿意度為優化目標進行了測試，結果如表1所列，與文獻中的結果相比，本文的測試結果要優.

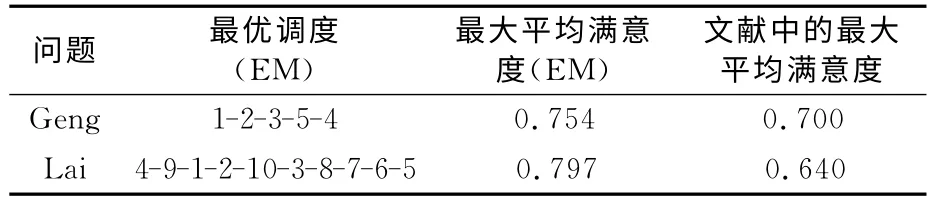
表1 文獻［10］和［11］中的實例測試結果

2）最小化最大模糊完工時間 在以最小化最大模糊完工時間為優化目標的測試里，采用了文獻［12］，［13］和［14］中的實例進行測試.因為文獻［13］和［14］中的問題是無等待模糊置換流水車間調度問題，所以這里只是用到了文中數據，未對結果進行比較.EM 算法的參數設置如下：種群數為20，算法的迭代次數為100，測試結果如表2 所列.

表2 文獻［12］，［13］和［14］中的實例測試結果

為了測試算法的收斂速度，這里給出了迭代次數和目標函數值之間的關系，依次如圖4所示，從圖4可以看到，針對這3個問題，本算法都有較快的收斂速度，針對文獻［12］和［13］中的問題，當迭代次數在10左右時，算法就已經收斂.對于文獻［14］中的問題，當迭代次數不到30時算法也已收斂.

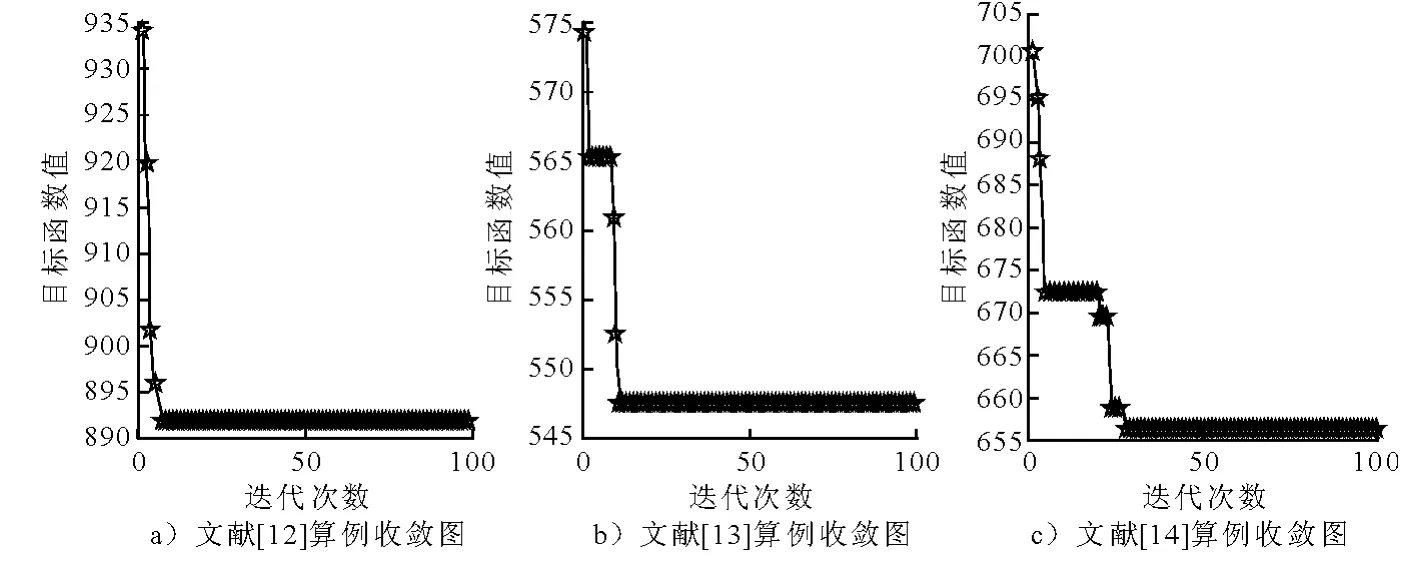
圖4 文獻［12］，［13］，［14］中算例的收斂圖

5 結束語

本文通過引入隨機鍵的方法，采用了一種元啟發式算法——類電磁機制（EM）算法求解了模糊流水車間調度問題，優化目標有最大化平均滿意度和最小化最大模糊完工時間.測試實例和結果顯示，類電磁機制算法能較好地求解模糊流水車間調度問題.在以后的研究中，將采用更多的測試實例進行驗證，并進一步提高EM 算法的優化性能.

［1］BALASUBRAMANIAN J，GROSSMANN I E.A novel branch and bound algorithm for scheduling flowshop plants with uncertain processing times［J］.Computers and Chemical Engineering，2002，26（1）：41－57.

［2］NEZHAD S，ASSADI R.Preference ratio－based maximum operator approximation and its application in fuzzy flow shop scheduling［J］.Applied Soft Computing，2008，8（1）：759－766.

［3］JAVADI B，MEHRABAD M S，HAJI A，et al.No－wait flow shop scheduling using fuzzy multi－objective linear programming［J］.Journal of the Franklin Institute，2008，345（5）：452－467.

［4］ HONG Tzungpei，WANG Tzutin.Fuzzy flexible flow shops at two machine centers for continuous fuzzy domains［J］.Information Sciences，2000，129（1－4）：227－237.

［5］WU Hsienchung.Solving the fuzzy earliness and tardiness in scheduling problems by using genetic algorithms［J］.Expert Systems with Applications，2010，37（7）：4860－4866.

［6］BIRBIL?˙I.Stochastic global optimization techniques［D］.Raleigh Thesis：North Carolina State University，NC，USA，2002.

［7］BIRBIL?˙I，FANG S C.An electromagnetism－like mechanism for global optimization［J］.Journal of Global Optimization，2003，25（3）：263－282.

［8］WU Peitsang，YANG Wenhung，WEI Naichieh.An electromagnetism algorithm of neural network analysis－an application to textile retail operation［J］.Journal of the Chinese Institute of Industrial Engineers，2004，21（1）：59－67.

［9］SAKAWA M，KUBOTA R.Fuzzy programming for multi－objective job shop scheduling with fuzzy pro－cessing time and fuzzy duedate through genetic algorithm［J］.European Journal of Operational Research，2000，120（2）：393－407.

［10］GENG Zhaoqiang，ZOU Yiren，Using genetic algorithm to solve fuzzy flow－shop scheduling problem［J］.Systems Engineering and Electronics，2002，24（6）：5－7.

［11］LAI Pengjen，SHU Minghung.Tardiness in fuzzy flow shop scheduling problems based on possibility and necessity measures［J］.Eighth International Conference on Intelligent Systems Design and Applications，Kaohsiung City，Taiwan，2008（26－29）：437－441.

［12］XU Zhenhao，GU Xingsheng.Flow shop scheduling problems under uncertainty based on fuzzy cut－set［C］∥International Conference on Natural Computation，Changsha，China，2005：880－889.

［13］徐震浩，顧幸生.不確定條件下具有零等待的流水車間免疫調度算法［J］.計算機集成制造系統，2004（10）：1247－1251.

［14］鄭 璐，顧幸生.含零等待模塊的存儲時間有限型混合模糊Flow shop生產調度問題［C］∥第五屆全球智能控制與自動化大會會議論文集（4），2004：2909－2913.