用動態不等時距灰色模型預測滑坡變形*

謝謨文 柴小慶 賈 寧

(北京科技大學土木與環境工程學院)

傳統的GM(1，1)模型［1］及其改進型［2-7］都要求數據序列為等時間間隔。然而由于天氣、人為以及不同變形階段的觀測頻率不同等原因，完全等時距的數據很難獲取。因此，建立不等時距的灰色模型具有更重要的現實意義。當前處理不等時距的方法有3種:插值法，生成新數列法［8-9］和構造逼近曲線法［10］。插值法由于人為地估計原始數據，模型的可信度不高。生成新數列法在生成新數列時默認了數據列差值與時間差的線性或二次拋物線關系。構造逼近曲線法充分利用有限的原始數據，不生成人為的“原始”數據，得出一條比較理想的逼近曲線，據此建立離散預測模型。

本研究以文獻［10］提出的采用構造逼近曲線的不等時距灰色預測方法為基礎，結合新陳代謝的思想，將動態不等時距灰色GM(1，1)模型應用于滑坡變形的預測，基于金坪子滑坡變形的實際監測資料，對其預測精度及可行性進行了充分的分析比較與論證。

1 動態不等間距灰色模型簡介

文獻［10］中的不等時距灰色模型是采用固定的1組數據列對后續多個時刻的數據進行預測。這種方式建模次數少，建立1次模型可以多次使用，但是從預測的角度看，每次采用最新的數據進行預測，能夠得到更理想的預測結果。因為隨著系統的發展，舊數據信息的意義將逐步降低，在不斷補充新信息的同時，及時去掉老數據，建模序列更能反映系統的現時特征。

設擬預測tn時刻的值，則取該時刻前最新的m維原始數列為

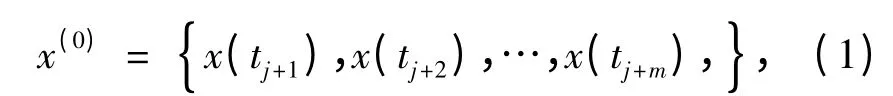
按照上述不等時距灰色預測模型，進行1次不等時距灰色預測后得到tn時刻的預測值x(0)(tn)。

采用動態模型，每來1個新值，就需要建立1個新的模型。灰色GM(1，1)模型的精度由后驗差比值C和小誤差概率P共同描述，要求C＜0.35，預測P＞0.95。

2 工程應用

烏東德水電站位于云南省昆明市和四川省涼山州交界的金沙江干流上。水庫正常蓄水位975 m，總庫容74億m3，裝機容量870萬kW，多年平均年發電量約387億kWh，屬特大型水電工程。

金坪子滑坡位于烏東德梯級河段下游右岸，上距烏東德壩址約900 m，其穩定現狀、變形趨勢、可能失穩方式及規模關系到烏東德水電站梯級開發的成立及河段內壩址的選擇，因而備受各界關注。為了客觀評價其工程影響，根據地質條件及變形特征，金坪子滑坡大致可分為5個區，如圖1所示。由于金坪子滑坡體Ⅱ區位于梯級河段的敏感部位，根據安全監測結果，該區變形一直在積累，因而必須對其穩定現狀、變形發展趨勢進行研究。

現選取金坪子滑坡Ⅱ區地表位移監測點TP09的實際監測數據為例，分別采用非動態和動態不等時距灰色模型對其垂直和水平位移進行預測分析。

為了方便計算對比，筆者基于Visual Studio.NET平臺及SQL Server數據庫，采用C#語言編制了非動態與動態預測模型及兩者比較程序。應用本程序，用戶僅需要選擇作為基數的時序數據以及預測日期序列，2種模型的預測結果數據表和對比曲線就能快速計算并顯示出來。

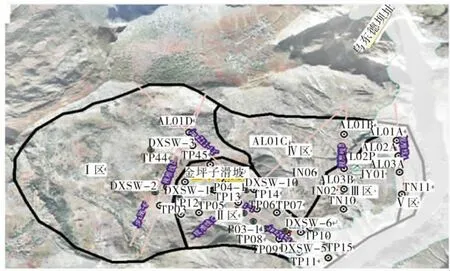
圖1 金坪子滑坡監測布置

表1給出了該測點2006年監測的14個垂直位移，可以看出，測值時間間隔不等。為了驗證并分析2種方法的預測精度，以前10個數據作為預測基數，采用模型程序中的2種方法預測后續4個日期的位移值。對于傳統的模型，只需用前10個數據建立1次預測模型，就可以依次對后續4個位移值進行預測。對于動態模型，首先用前10個數據建立預測模型，預測6月20日的測值，然后去掉第1個數據，添加第11個監測值(或預測值)進來，建立預測模型，計算7月30日的位移值……如此進行下去，直到預測出11月1日的位移值為止。

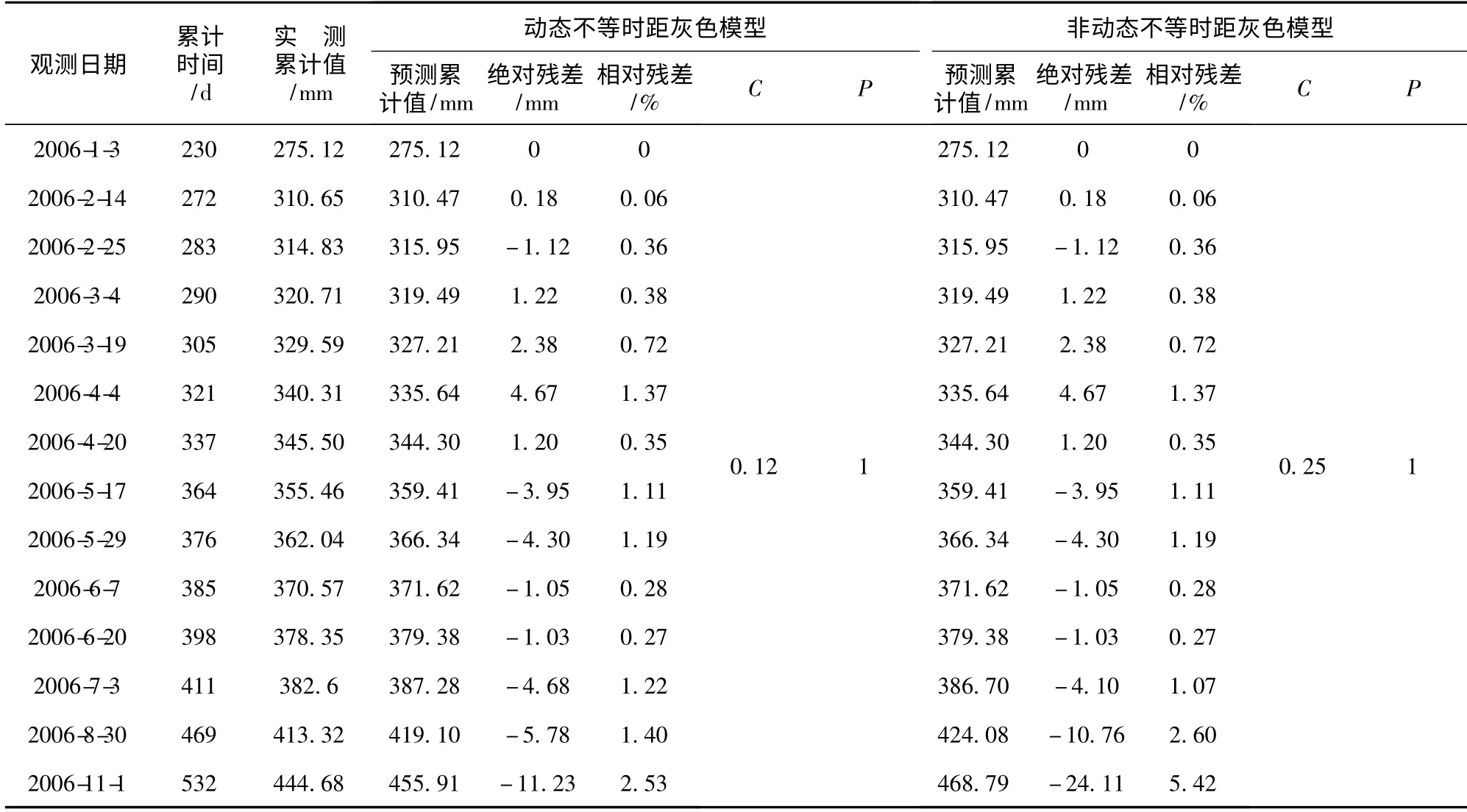
表1 TP09點垂直位移真實值與預測值比較

表1中列出了2種模型的垂直位移預測值及殘差檢驗參數。從后驗差比值和小誤差概率可以看出，2種模型的預測精度都達到了要求。與非動態模型相比，動態不等時距灰色模型的后驗差參數遠小于非動態模型，說明其預測精度更高。

從表2可以看出，采用2種方法對水平位移進行預測的精度也都合格。動態預測模型精度更高。

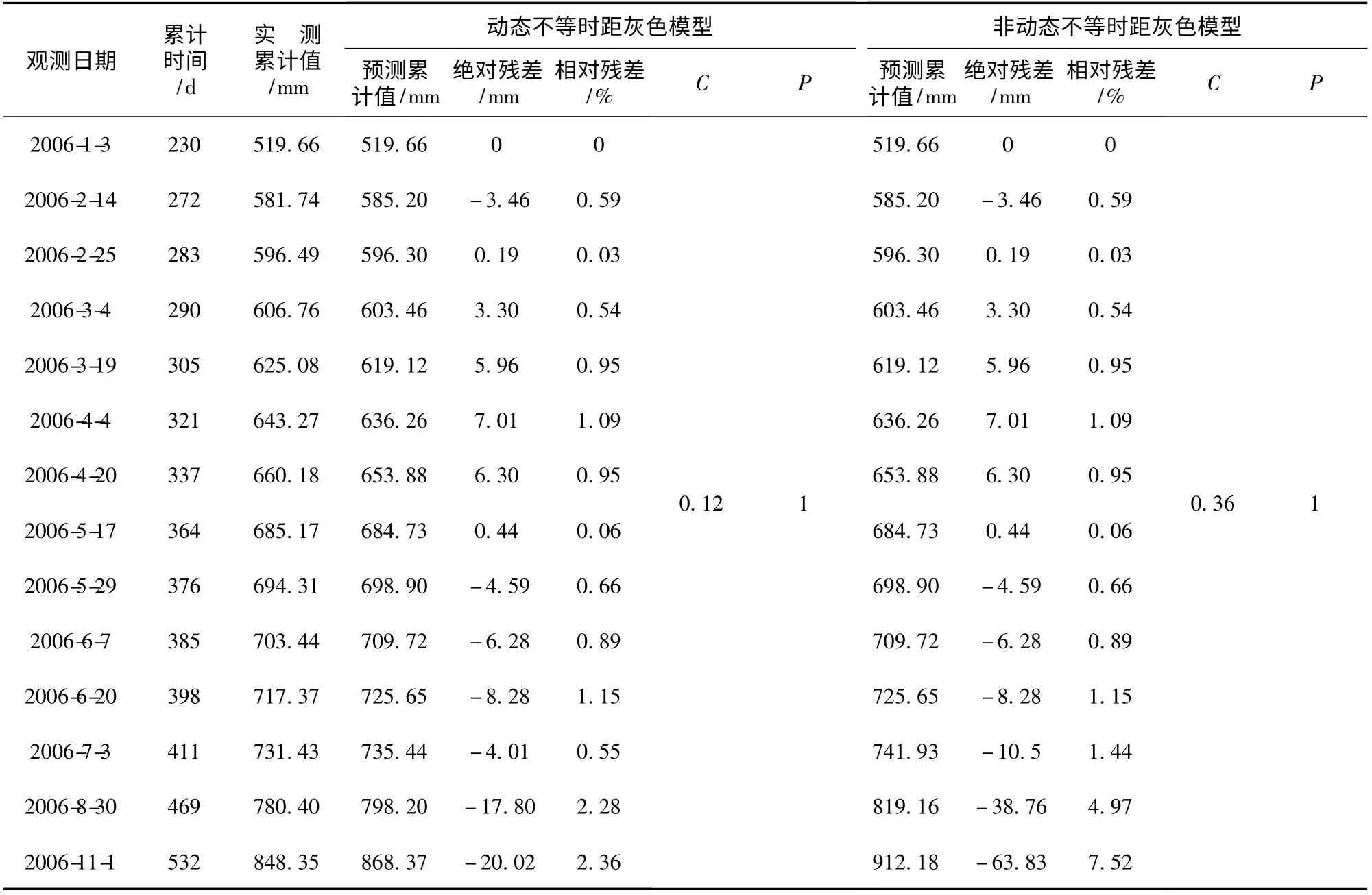
表2 TP09點水平位移真實值與預測值比較

參照表1，表2還可以發現，第13和14個位移值由于時間間隔較大，預測的殘差也相對較大。這是因為灰色模型本身是基于等時距序列建立的，且為指數模型，對于時間間隔嚴重不等的情況，建立的模型的精度會有所下降。因此在進行監測時，應盡可能等時距，以便保證模型精度。

3 結論

利用逼近曲線法不等時距灰色預測模型對金坪子滑坡位移觀測成果進行了預測，獲得了滿意的預測結果。與非動態模型相比，動態不等時距灰色模型采用最新監測數據進行建模，精度明顯提高，能夠滿足實際工程應用。

基于Visual Studio.NET平臺及SQL Server數據庫，采用C#建立了及預測程序，大大提高了建模及預測的效率，且操作簡便，具有很強的實用價值。

動態不等時距灰色模型在短期內對滑坡位移的預測精度較高，如果要進行長期預測，還需要對模型作必要的修正。

［1］ 鄧聚龍.灰色系統理論教程［M］.武漢:華中理工大學出版社，1990.

［2］ 劉 輝，謝俊峰，陳建平.應用灰色系統理論預測界牌關隧道拱頂沉降［J］.巖土工程，2008(2):129-130.

［3］ 肖海平，陳蘭蘭.灰色理論模型在礦山變形監測中的應用［J］.金屬礦山，2009(1):154-161.

［4］ 李秀珍，孔紀名，王成華.中心逼近式灰色GM(1，1)模型在滑坡變形預測中的應用［J］.工程地質學報，2007，15(5):673-676.

［5］ 焦建新，袁 博，楊永興.基于穩健GM(1，1)模型的基坑變形監測數據處理方法［J］.礦山測量，2007(4):11，12，19.

［6］ 黃 銘，葛修潤，王 浩.灰色模型在巖體線法變形測量中的應用［J］.巖石力學與工程學報，2001，20(2):235-238.

［7］ 劉思峰，鄧聚龍.GM(1，1)模型的適用范圍［J］.系統工程理論與實踐，2000(5):121-124.

［8］ 秦亞瓊，魏麗敏.不等時距GM(1，1)模型預測地基沉降研究［J］.武漢理工大學學報:交通科學與工程版，2008，32(1):134-1371.

［9］ 李恒凱，劉德兒.基于牛頓插值的建筑物沉降灰色預測模型研究［J］.工程勘察，2010(2):57-61.

［10］ 胡 斌，曾學貴.不等時距灰色預測模型［J］.北京交通大學學報，1998，22(1):34-38.