大規模綜合電力系統穩定性分析

賀開華，魏建勛

（1. 海軍駐湖南地區軍事代表室，湘潭 411101；2. 湘電集團有限公司，湘潭 411101）

大規模綜合電力系統穩定性分析

賀開華1，魏建勛2

（1. 海軍駐湖南地區軍事代表室，湘潭 411101；2. 湘電集團有限公司，湘潭 411101）

本文的目的是提出一種大規模綜合電力系統穩定性的分析方法，詳細闡述在研究該系統時所要面臨的基本問題，并且針對該類系統，給出了大、小信號穩定性的定義，系統建模和仿真分析方法以及系統穩定性的分析方法。

綜合電力系統 大規模 穩定性

0 引言

艦船綜合電力系統是非常典型的基于電力電子功率模塊的電力系統，與傳統艦船電力系統相比，在該系統中，發電、配電、用電由各種電力電子裝置實現的。各種AC/DC，DC/DC，DC/AC等變換器分別用來作為電源、負載或分布式變換器以適應不同電壓等級和電制的電能需求。

在研究該系統時一個最基本的問題就是穩定性，本文重點關注該系統的穩定性分析問題。到目前為止，該系統穩定性分析的基本問題還未完全解決。以前的研究工作用的都是系統元件的平均、線性化以及降階模型，這主要是由于系統的復雜性以及現有的仿真軟件無法處理如此大系統的精確模型仿真。

而且，對該系統存在的小擾動、頻域建模和仿真的精確性和有效性問題，在文獻[4]中已表明相同的一個DC/DC變換器，狀態空間平均模型具有不穩特征根，而精確的線性時變模型卻是穩定的，這主要由于系統矩陣病態而引起的。因此，如果不考慮額外條件，狀態空間平均模型是不能使用的。從這個例子中可以得出一個結論，建模技術對系統穩定分析結果影響很大，可能導致錯誤的結論。然而，對于大信號穩定性分析，使用可靠的大信號模型進行時域仿真是必然的。

在本文中，介紹了綜合電力系統和它的動態特性，詳細闡述了針對該類系統的大、小信號穩定性的定義。此外，還討論了系統建模、仿真和穩定性分析方法。此外本文還介紹了提高系統穩定性的方法，最后總結研究結論。

1 綜合電力系統的定義

本文的研究對象是基于電力電子功率模塊的綜合電力系統，如圖1所示，系統中的主電源是三相交流發電機，主推進器是系統中的最大負載，約占系統總容量的80%。與傳統艦船電力系統日用負荷大都直接從交流主母線獲電不同，綜合電力系統中的日用負荷電能都是從各種電力電子變換裝置獲得的。即三相發電機輸出通過母排直接給大功率推進負荷和AC/DC變換器供電，AC/DC變換器輸出再通過各種電壓等級的DC/DC或DC/AC變換器給負載供電。在綜合電力系統中存在著大量的DC/DC或DC/AC變換器，它們有的作為電源，有的作為負載使用。

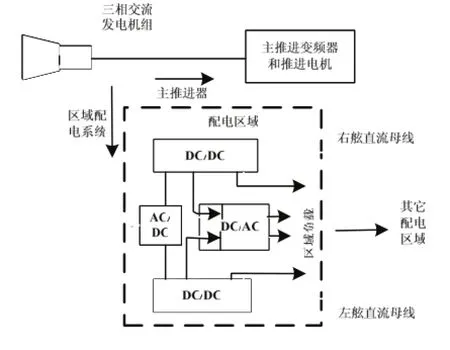
圖1 基于電力電子變換模塊的艦船綜合電力系統示意圖

因此，精確的全綜合電力系統仿真必須建立系統中每個變換器、控制器以及負載的等效電路模型，這將是一個龐大的工程，且時間常數從納秒一直變化到秒，這明顯要求非常長的計算時間和大量的計算機內存。因此目前看來，綜合電力系統中小規模子系統的精確仿真才是現實的。小規模子系統劃分的規則最好是包含一個源和所有連接該源的負載。這種劃分方法包含了源和負載以及負載與負載之間的相互作用。這里的“源”指的是所有供給相同母線電能的并聯電源，“負載”指的是類似水泵，風扇以及電機驅動器等的獨立負載模塊。一個實際的子系統就是綜合電力系統的一部分，例如，它可以是包含一個DC/DC電源變換器，然后通過電纜輸出一定電壓等級的直流電到幾個更小的母線，每段母線都給幾個負載供電。典型的，設計時對DC/DC變換器的輸出阻抗最大幅值和相位以及負載的最小阻抗幅值以及相位都作了要求。文獻[3]闡述源和負載的阻抗幅值要求，阻抗要求的意義將在下節中闡述。

2 穩定性的定義

對于線性、非線性、離散以及連續系統都有不同的穩定性定義。線性系統的穩定性分析通常采用以下幾種經典方法：勞斯-胡爾維茨判據，根軌跡、伯德圖以及奈奎斯特判據。對于線性、非線性系統，另外一種非常有名的方法是李雅普洛夫第二法。但對于非線性系統構造李雅普洛夫函數是個難點。因此，在確定大信號穩定性時，希望得到更多敘述詳細的定義。非線性系統穩定性分析須考慮系統的初始條件、外部輸入以及它們對系統中非線性元件的影響。以我們目前所了解的，現在還沒有一種通用的分析非線性系統穩定性的方法。之前的研究工作大都是基于線性系統穩定性的分析方法[1,2]。在文獻[2]中，分析穩定性時，R、L、C以及DC元件都采用小信號線性化模型，用相角裕度去確定系統的穩定性。文獻[1]闡述了綜合電力系統的設計依據，文獻利用源和負載的輸出，輸入阻抗分析了系統的穩定性。文獻[1]中通過仿真和試驗驗證完善了大信號穩定性分析。

本文中穩定性的定義參考李雅普洛夫的漸進穩定性，然而，我們還不能找到一種對每個獨立負載或者包含源和負載的子系統都適用的李雅普洛夫函數，而是考慮這些子系統的輸入、輸出電壓和電流的條件。我們認為失穩的一種形式是輸入或者輸出電壓、電流偏離了期望值允許的范圍之外，而在預定的時間內又無法回到允許的范圍之內，例如無界。無界性在電力電子電路中往往是不可預測的，例如在Boost變換器中開關失敗，將導致母排短路。這種類型的非線性失穩是不能用傳統的線性系統相角和增益裕度來預測的。如果沒有適當的保護和控制電路，這種類型的失穩往往會導致整個系統故障。振蕩是另外一種無法利用傳統控制系統穩定性測量手段可以預測的非線性，必須通過檢測實際系統的硬件和電路才能發現。振蕩主要是缺乏阻尼機構引起的。長期振蕩也會因為熱效應導致元件故障。電力電子系統中另外一種失穩表現稱為混雜，它在系統中主要表現為一個或多個元素的偽隨機函數。“混雜”的一種形式如圖2所示，由功率電子開關產生的確定的諧波噪聲，它與外界噪聲一起作用于DC/DC變換器PWM電路反饋環的控制信號上，從而造成PWM占空比的隨機變化。

如前所述，本文所考慮的系統，由AC/DC、DC/DC變換器以及包含DC/DC、DC/AC等變換器的負載組成，這些變換器產生各種電壓等級和電制的電源以供給所需的負載。一種確定這種系統穩定性的可行方法是通過仿真。那么，一個最重要的問題隨之變成：需要什么樣的DC/DC、DC/AC變換器和負載模塊模型和需要頻域還是時域的分析方法？一些通常需要考慮的仿真類型，例如大擾動、小擾動以及穩態仿真，目前最普遍、流行的方法是狀態空間平均和小信號線性化。

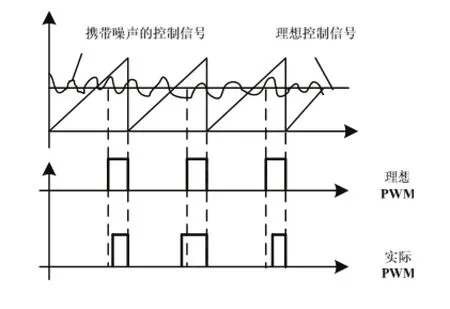
圖2 混雜失穩模擬實例

眾所周知，通常使用的DC/DC變換器，例如Buck，Boost，Buck-Boost，在電流連續時有兩種運行模式，斷續時有三種。如果變換器開關頻率與控制系統動態相比足夠高，那么就可以用狀態空間平均模型來描述它們。通常，設計時變換器增益的交叉頻率要比開關頻率至少低一個數量級，因此狀態空間平均模型對DC/DC變換器的小信號分析是完全適用的。狀態空間平均等效電路模型是一個非線性、連續的等值電路，可以表示原本非線性的脈沖（離散）系統，這種模型對大小信號都是適用的，但通常只是模擬了變換器和濾波器本身，并沒有模擬控制器的動態和限制。系統中母線故障、機械失靈，負載改變，電力電子元件故障等都可能引起大信號偏差。如果不考慮大信號偏差，通常的做法是線性化非線性狀態空間平均模型。但系統模型線性化的結果只對小信號分析適用，例如母線電壓、電流、電力電子元件以及負載的微小變化。什么樣的擾動算是小擾動取決于系統模型中的其它參數。

線性化去除了擾動的乘積效應，但是，當此類效應由于大信號變化在系統中變得重要時，線性化模型就無效了。在設計電力電子變換器的控制電路以及濾波器時，小信號模型是最佳選擇，然而在分析系統穩定性時，還是有局限性的。

3 穩定性分析的仿真考慮

使用線性化狀態空間平均模型分析系統穩定性的前提依賴于系統保護、限制電路的可靠性以及假設整個系統中的每一個獨立的電源和負載在穩定邊界內能阻止大信號失穩。小信號穩定分析通常的方法是建立小信號等效電路并仿真確定系統的穩定性。系統穩定的充要條件是各級子系統均穩定。然而，問題是這種仿真需要嗎？文獻中的經典研究工作認為這種類型的仿真是沒有必要的。Middlebrook在文獻中認為子系統中的電力變換模塊都是單獨設計的，本身都是穩定的，這些電力變換模塊組成系統后之所以有可能出現不穩定，是由于系統的前、后級之間阻抗不匹配造成的。因此，利用子系統源的輸出阻抗和總的負載阻抗就可以確定系統的穩定性，圖3所示為系統小擾動穩定的阻抗定義。利用雙端口理論，如果系統的閉環增益T(s)=Zs/ZL滿足奈奎斯特判據，那么系統是穩定的。從控制理論的角度，可以通過判斷環增益ZsYL的Nyquist曲線是否包圍復平面上的（-1, j0）點來判斷系統穩定性。因此，系統穩定性的一種更簡單、更直接的判據是在工作頻率范圍內都有|ZsYL|＜1，這不僅能確保級聯系統的穩定性，還能減小因子系統間相互作用而造成的整個系統性能的退化，這就是Middlebrook輸入輸出阻抗判據。很顯然，Middlebrook輸入輸出阻抗判據的條件過于保守，它要求在工作頻率范圍內都有前級的輸出阻抗小于后級的輸入阻抗，系統才是靜態穩定的，這種要求在實際的系統中是很難做到的。為了克服Middlebrook阻抗判據造成的人為保守因素，各種實用判別方法應運而生，其中包括禁止域法和導納空間法等。

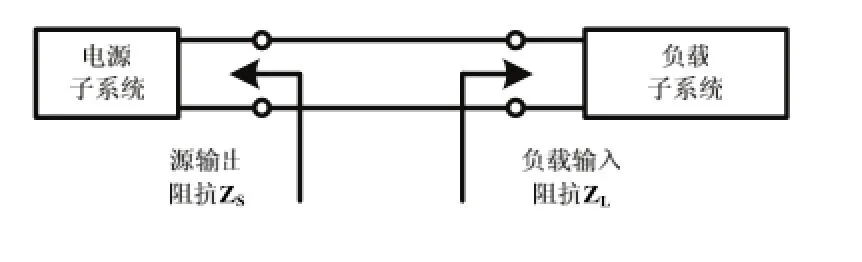
圖3 源輸出阻抗和負載輸入阻抗定義

對于多電源和負載并聯的獨立系統，一旦所有負載支路的并聯輸入阻抗和所有電源的并聯輸出阻抗確定之后，就可以用Middlebrook阻抗判據判斷系統的穩定性。系統電源、負載以及電纜阻抗如圖4所示。

現在，如圖4中的A點作為穩定性分析的位置，那么該處的小擾動穩定性取決于T(s)是否滿足奈奎斯特穩定判據，這里T(s)表達式為：

如果系統被認為是一個大信號模型，那么顯然線性化后的狀態空間模型是無效的。那么全系統的精確時域仿真必須使用包含保護電路、控制系統動態以及限幅等的非線性模型。如果不能對單個電源和負載的保護電路、控制系統動態以及限幅等非線性進行精確模擬，那么系統的仿真分析結果是不正確的。

圖4 小信號分析的阻抗定義

4 負阻抗特性引起的不穩定性

艦艇綜合電力系統中的很多負載（例如推進器）往往被控制調節成恒功率負載。雖然恒功率負載的瞬時電阻是正的，但是增益電阻卻是負的。實際上，流過恒功率負載的電流隨著電壓的增加而減小，隨著電壓的減小而增大，這導致恒功率負載具有負阻抗特性，這是一個不穩定的因素，稱之為負阻失穩。在有的文獻中，已詳細闡述了在多功率變換器系統中有恒功率負載所引起的系統穩定性問題。并且給出了在設計綜合電力系統時如何解決由負阻引起的系統失穩問題。

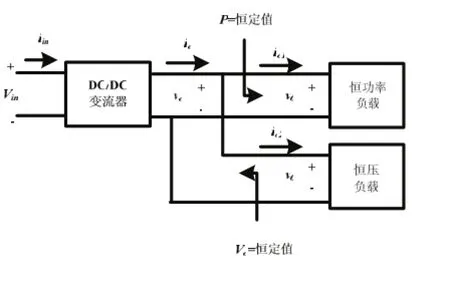
圖5 DC/DC變換器的等效恒功率和恒壓負載

如圖5所示，通常在綜合電力系統中存在兩種類型的電力電子變換器，一種表現為恒功率特性，功率變換器能在一定的電壓范圍（Vomin≤Vo≤Vomax）內提供恒功率，而不致于失穩。另一種負載運行時需要恒定電壓。文獻給出了該系統穩定的充分條件：

在上式的穩定條件下，可采用傳統的PI控制器控制DC/DC變換器而不使系統失穩。也就是說，若（2）式條件滿足，則在DC/DC變換器的輸出端可以同時給恒壓和恒功率負載供電。但是若（2）式條件不滿足，系統不穩定。在文獻[2]中，提出了一種變模式非線性控制器能使DC/DC變換器帶恒功率負載工作時在預定的電壓范圍內穩定。

5 結論

總之，對于小信號穩定性研究，無需建立整個系統的小信號等效電路。本文所闡述的阻抗判據方法可以節省大量時間，是一種更經濟的方法。然而它需要獲得電源的輸出阻抗，負載的輸入阻抗。若在實驗室具備這樣的系統，那么這些阻抗很容易得到，或者通過制造商直接獲得。

在另一方面，對于大信號穩定性研究，利用可靠的大信號模型進行時域仿真是必須的。而且這些系統在設計和制造之后最好是通過時域仿真來檢驗它們的穩定性。這些仿真分析的限制主要在于實際控制和保護電路的動態特性，包括欠壓閉鎖，過壓和過流保護，以及電磁路飽和、泄露、半導體操作、溫度變化、老化以及突然故障所引起的非線性。對于大系統的大信號穩定性仿真，在建模和仿真中都需要花費大量的時間。

[1] Middlebrook R D．Input filter considerations in design and applications of switching regulators[C]. IEEE IAS Annual Meeting，Piscataway，1976, 1:158-162.

[2] Middlebrook RD，Cuk S．A general unfied approach to modeling switching-converter power stages[C]．IEEE PESC，NewYork：1976, 1:23-25.

[3] Brown A R，Middlebrook R D．Sampled-data modeling of switching regulators[C]. IEEE Power Electron. Specialist Conf．Minskerski：IEEE，1998, 2:346–369.

Stability Analysis of Large Scale Integrated Power System

He Kaihua1，Wei Jianxun2

（1. Naval Representives Office in Hunan, Xiangtan 411101, China; 2. Xiangtan Electric Group Co. Ltd, Xiangtan 411101, China）

This paper proposes a method for analyzing the stability of a large scale integrated power system (IPS). The basic issues of the study are presented. Aimed at this kind of system, the definitions of large and small signal stability, the method of system level modeling and simulating, and the way of analyzing system stability are also introduced.

integrated power system; large scale; stability

TM712

A

1003-4862（2013）05-0027-04

2012-10-15

賀開華（1966-），男，高級工程師。研究方向：電力系統保護與控制。