《結(jié)構(gòu)力學(xué)》一則習(xí)題“怪異”結(jié)果的分析
王廣利
(黎明職業(yè)大學(xué)土木建筑工程學(xué)院,福建泉州 362000)
在《結(jié)構(gòu)力學(xué)》[1]中有一則習(xí)題,要求畫出簡支梁在均布的分布力偶作用下的剪力圖和彎矩圖,如圖1所示.
本習(xí)題的求解并不難,利用平衡條件先求出約束反力,得FAY= - m,F(xiàn)B= - m(負(fù)代表與假定的指向相反),如圖2所示.再用截面法截開距A端為x的任意截面,取左邊為隔離體(如圖3所示),并取平衡,得此截面上剪力和彎矩的表達(dá)式分別為(1)式和(2)式,此二式即為梁的剪力方程和彎矩方程(將A端視為坐標(biāo)原點(diǎn)).
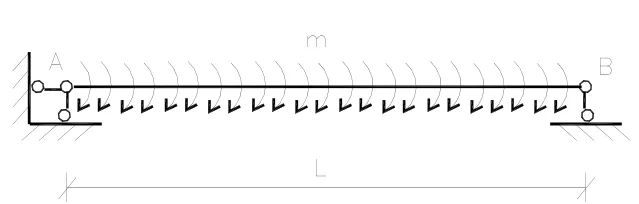
圖1
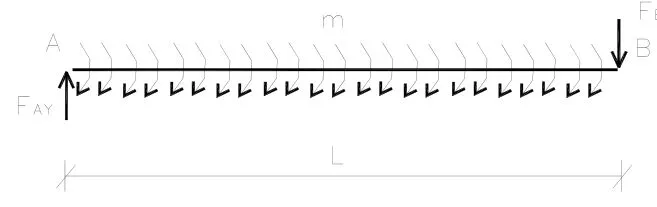
圖2
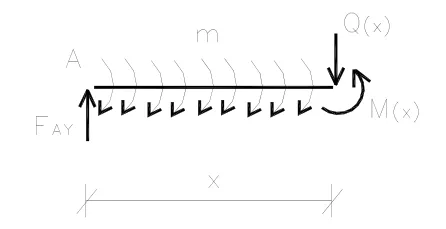
圖3

將已有結(jié)果FAY= - m,代入(1)式,得Q(x) = - m,進(jìn)一步可得M(x) = 0.于是可得梁的剪力圖和彎矩圖,如圖4(a)和圖4(b)所示.

圖4


圖5是直桿中截出的長度為dx的微元,這個(gè)微元上作用的荷載不僅有分布力q(x)(規(guī)定向上為正),還有分布力偶m(x)(規(guī)定順時(shí)針為正)。

圖5
由∑Fiy=0可得
Q( x)+ q( x)· dx= Q( x)+ dQ( x),從而得到
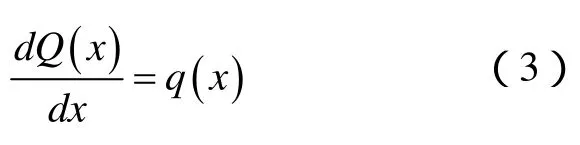
由∑MC=0可得

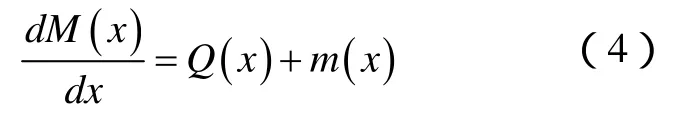
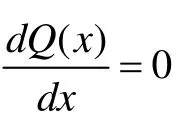
2 結(jié)論與討論
(1)從式(4)可以看出,分布力偶對彎矩的影響類似于集中力;
3 結(jié) 語
在工程結(jié)構(gòu)實(shí)際問題中,幾乎不會(huì)出現(xiàn)分布力偶荷載作用的情況,因此,在《結(jié)構(gòu)力學(xué)》教材中沒有涉及分布力偶荷載,但作為教學(xué)一線的力學(xué)工作者則有必要對力學(xué)原理和方法的前提條件及適用范圍有一個(gè)清晰的認(rèn)識(shí).
[1]袁駟.定性結(jié)構(gòu)力學(xué)(網(wǎng)絡(luò)課程),清華大學(xué)結(jié)構(gòu)力學(xué)精品課程網(wǎng)站.http://www.civi l.edu.cn/smsolver/user/Qual it ySM/index.htm.
[2]孫訓(xùn)方,等.材料力學(xué):第三版[M].北京:高等教育出版社,1994.

