計及風機無功約束的電壓穩定性分析

劉 鋮，蔡國偉，楊德友，孫 琦

（1.東北電力大學電氣工程學院，吉林 132012；2.華北電力大學電氣與電子工程學院，北京 102206）

近年來，風力發電發展迅速。風能作為一種綠色的可再生能源已成為世界能源的重要組成部分。隨著我國能源政策的調整，風電展現了廣闊的發展前景。

風能具有隨機性、間歇性等特點，隨著風電機組容量和風電場規模增大，迫切需要研究大型風電場并網后對電力系統穩定的影響[1-2]。風電的接入將會給系統電壓穩定帶來影響，如何合理評估含風電場系統的電壓穩定問題是極其有意義的。

目前，針對風電場接入系統的電壓問題已進行了大量的論述。文獻[3]提出基于PV曲線的風電場接入系統穩態分析方法及兩個風電場同時接入系統的分析方法，分析了風電場接入系統的電壓要求及風電場運行對區域電網網損影響。文獻[4，5]基于連續潮流法對異步機風電場與基于雙饋感應電機（doubly-fed induction generator，DFIG）的變速風電場接入電網后系統的靜態電壓穩定裕度進行比較了研究。

但是，這些文獻重在比對不同風機類型對系統電壓穩定的影響，均沒有涉及考慮雙饋感應風機風電場無功限制對系統電壓穩定的影響，且未深入分析失穩原因。

本文對基于雙饋感應風力發電機組風電場進行研究，建立雙饋風機的數學模型，通過繪制風電場接入點PV曲線，分析采用不同無功限制下雙饋風力發電機組風電場接入系統后的靜態電壓穩定性，同時通過分岔理論分析失穩類型和對風機接入系統裕度的影響。結果表明，DFIG考慮功率極限對電壓穩定裕度有一定的影響且影響分岔類型，考慮DFIG發生的不同分岔可以更真實地揭示系統失穩原因和提供實際裕度。

1 風力發電機組的穩態數學模型

雙饋異步風力發電機等值電路如圖1所示[6]。

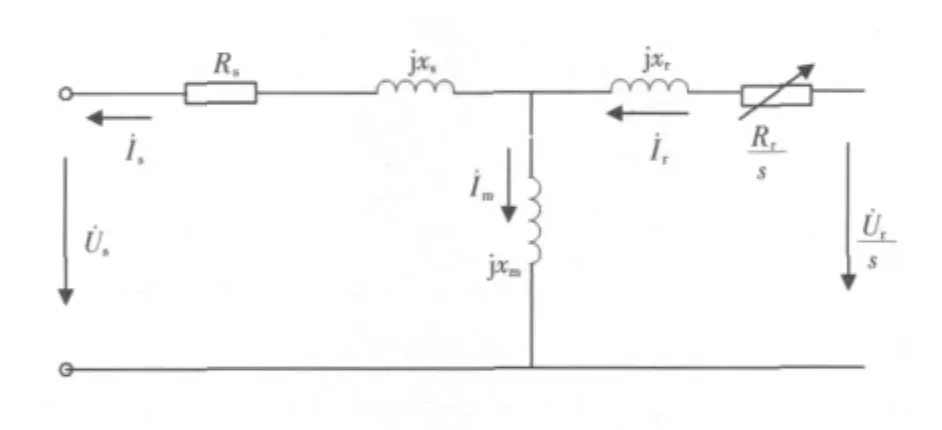
圖1 雙饋異步風力發電等值電路示意Fig.1 Equivalence circuit of a DFIG wind

注入系統總有功Pe由兩部分組成，一是定子繞組的有功Ps，另一部分是轉子繞組發出或消耗的有功Pr。

由于變流器吸收或發出的無功很小，可近似認為風電機組無功功率Qe等于定子繞組無功功率Qs，所以風電機組注入系統有、無功功率為

風電機組注入系統轉子繞組的有功功率[7]為

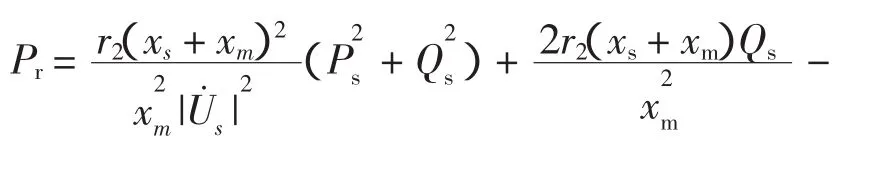
定子側有、無功運行范圍主要受變流器轉子側電流限制，可表示為

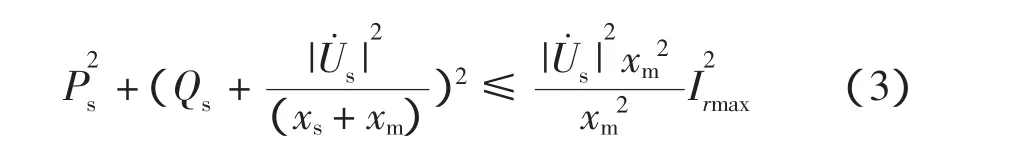
式中，Irmax是變流器電流限制值。

將式（1）分別代入式（2）和式（3），可得

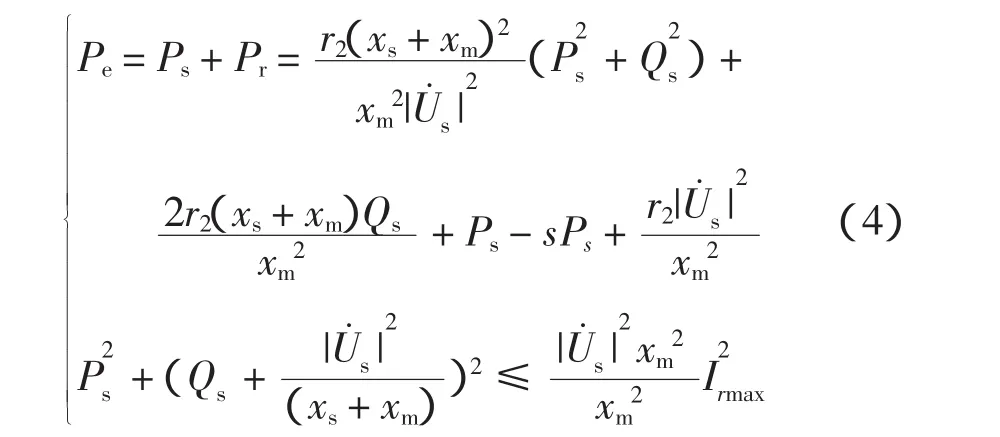
相應的無功功率極限可由式（4）求得。

2 含風電系統的分岔點類型分析

包含上述風電系統的電力系統穩態數學模型可寫成

式中：x為狀態變量；y為代數量，包括電壓幅值和相角；λ為負荷參數。

電力系統分岔分析方法可分為靜態分岔分析和動態分岔分析兩種。下面介紹兩種在靜態分岔分析中經常遇到的分岔：鞍結分岔（saddle induced bifurcation，SNB）和極限誘導分岔（limit induced bifurcation，LIB）。并將二者用于含風電的分析中。

2.1 鞍結點分岔

鞍結分岔[8]的條件為

或

式中，v和w分別為右、左特征向量。

圖2所示的是通常的PV曲線，在點SNB發生鞍結分岔。

2.2 極限誘導分岔

極限誘導分岔[2，8-10]點可定義系統的解為

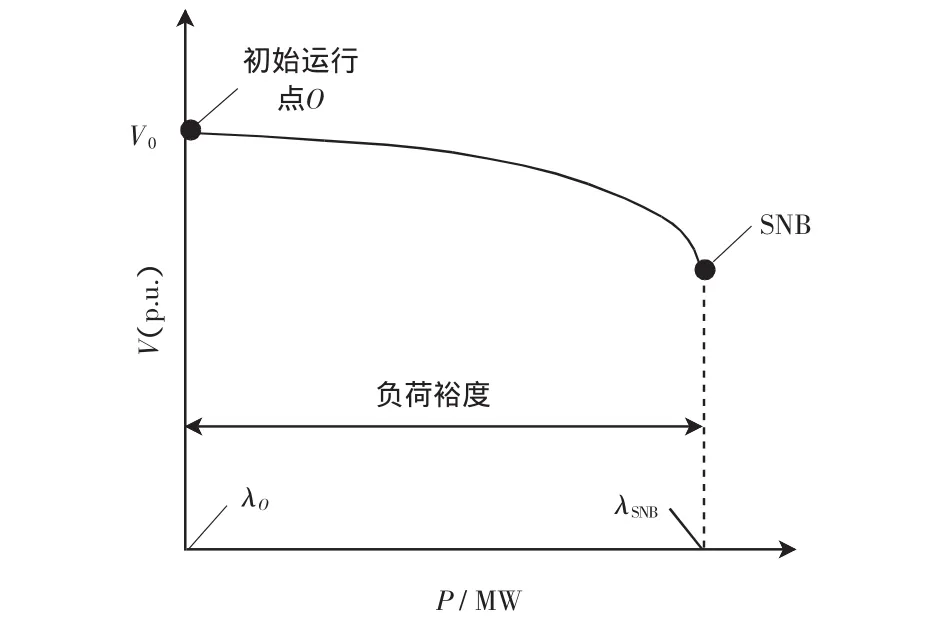
圖2 鞍結分岔Fig.2 Saddle node bifurcation

式中，ρ（y）是附加限制條件，對于平衡節點和發電機PV節點條件為

或對負荷節點應滿足條件為

極限誘導分岔是發電機到達無功極限引起的，圖3給出了發電機的PV曲線圖。Vs為給定值，Q=Qlim為發電機處于無功極限狀態下的PV曲線。隨著負荷增加，電壓水平會降低。如圖3的A點，發電機到達無功極限，對于1，點A位于曲線下半部，誘發系統突然電壓崩潰。當系統運行在另一情況：如虛線2所示。運行點位于曲線上半部，即不會發生極限誘導分岔。

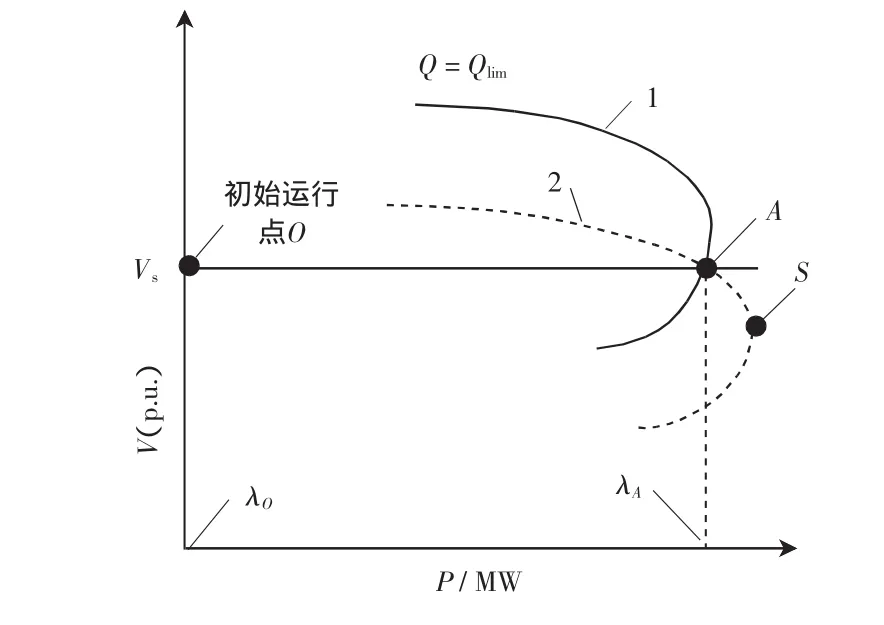
圖3 極限誘導分岔Fig.3 Limit induced bifurcation

本文在計及雙饋風機無功極限影響下，對雙饋風機風場的分岔類型作判別。由于DFIG具有一定的無功支撐作用，能夠基本維持風場并網點電壓恒定不變，可近似把風力發電機節點等同于同步發電機節點考慮，利用文獻[8]對LIB的定義判別風場分岔類型。

3 風電場系統的靜態電壓穩定分析

在風電系統靜態電壓穩定性分析中，目前使用比較廣泛的是PV曲線法[3]。它通過建立節點電壓和一個區域負荷的關系曲線，指示區域負荷水平導致整個系統臨近電壓崩潰的程度[3-5]。

連續潮流是電壓穩定性分析的有力工具，可以克服潮流方程在接近穩定極限運行狀態時的收斂問題。連續潮流法從初始穩定工作點開始，隨著負荷緩慢變化，沿相應PV曲線對下一工作點進行預估-校正，直到勾畫出完整的PV曲線連續潮流計算方法。

應用PV曲線方法分析風電場的靜態電壓穩定性時，考慮風電注入系統的功率對電壓穩定性的影響，則P代表的是風電場的有功功率，V取風電場接入點電壓，V也可以是其他節點或機端等關鍵節點電壓。通過連續潮流獲得風電場關鍵節點的PV曲線，進而分析風電場的靜態電壓穩定問題。

4 算例分析

4.1 風電場及系統簡介

采用IEEE30節點標準測試系統作為算例系統[10]，風電場通過升壓變壓器和135 kV線路接入系統（見圖4）。

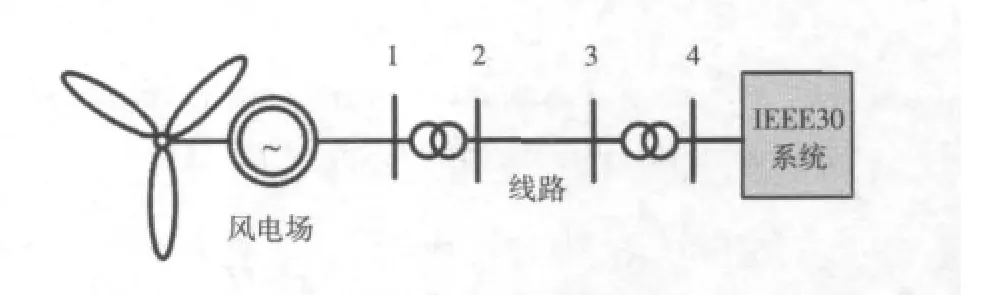
圖4 風電場接入的IEEE30節點系統結構Fig.4 IEEE30 node system structure containing wind farm

選擇節點4為系統接入點。雙饋感應風力發電機組風電場單機容量1.5 MW，參數見文獻[11]。系統及風電場均采用標么值，基準容量100 MVA，基準電壓為額定電壓。風電場地區空氣密度為1.224 5 kg/m3，風力機的掃掠面積為1 840 m2。

4.2 考慮DFIG風機無功功率極限限制的風機PV曲線分析

當V=0.9 p.u.時，某1.5 MW DFIG風機無功出力限制曲線如圖5所示。

根據上面計算出的DFIG風機無功出力上下限，考慮在DFIG風機功率因數設定不同時，繪制并網點電壓隨風電場有功出力增加的PV曲線，如圖6所示。

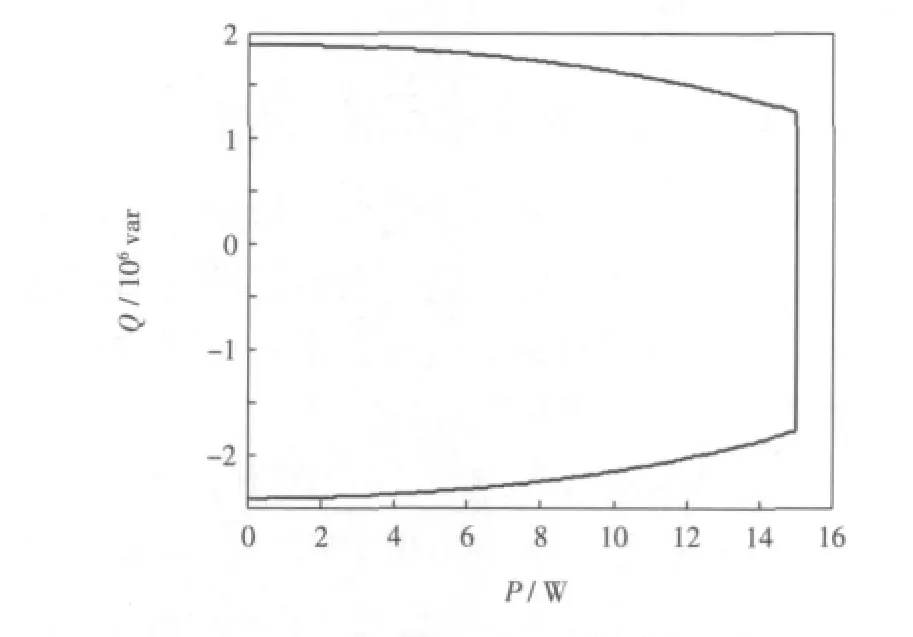
圖5 某1.5 MW DFIG風機可用無功出力輸出范圍Fig.5 Schematic diagram of available reactive power output of some kind DFIG with rating of 1.5 MW

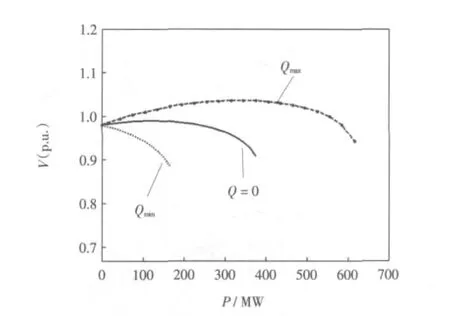
圖6 1.5 MW DFIG風機風場不同無功出力下的風機PV曲線Fig.6 PV curvs of availables reactive power output of some kind DFIG with rating of 1.5 MW

由圖6可知，無功輸出越大，風機接入裕度越大，但是同時也會造成風電場接入點電壓升高，當無功輸出為Qmin時，節點電壓隨風機注入功率增加而降低，造成電壓越限，相比在無功出力為0時，即功率因數為1，電壓波動較小，且相對平穩。可見風機應采用功率因數為1的運行方式，與實際中通常的運行方式較為吻合。

當風電場運行在Qmin、Qmax時，風電場并網節點電壓PV曲線分別如圖7所示。

由圖7可見，對于DFIG運行在Qmin情況，隨著風電場注入功率的增加，引起了并網點電壓下降。相反，對于Qmax的情況，風電場功率增加引起了電網并網點電壓的升高。說明DFIG風電場的無功對系統并網節點的電壓有著重要的影響，因此DFIG的無功出力運行方式不可忽略。

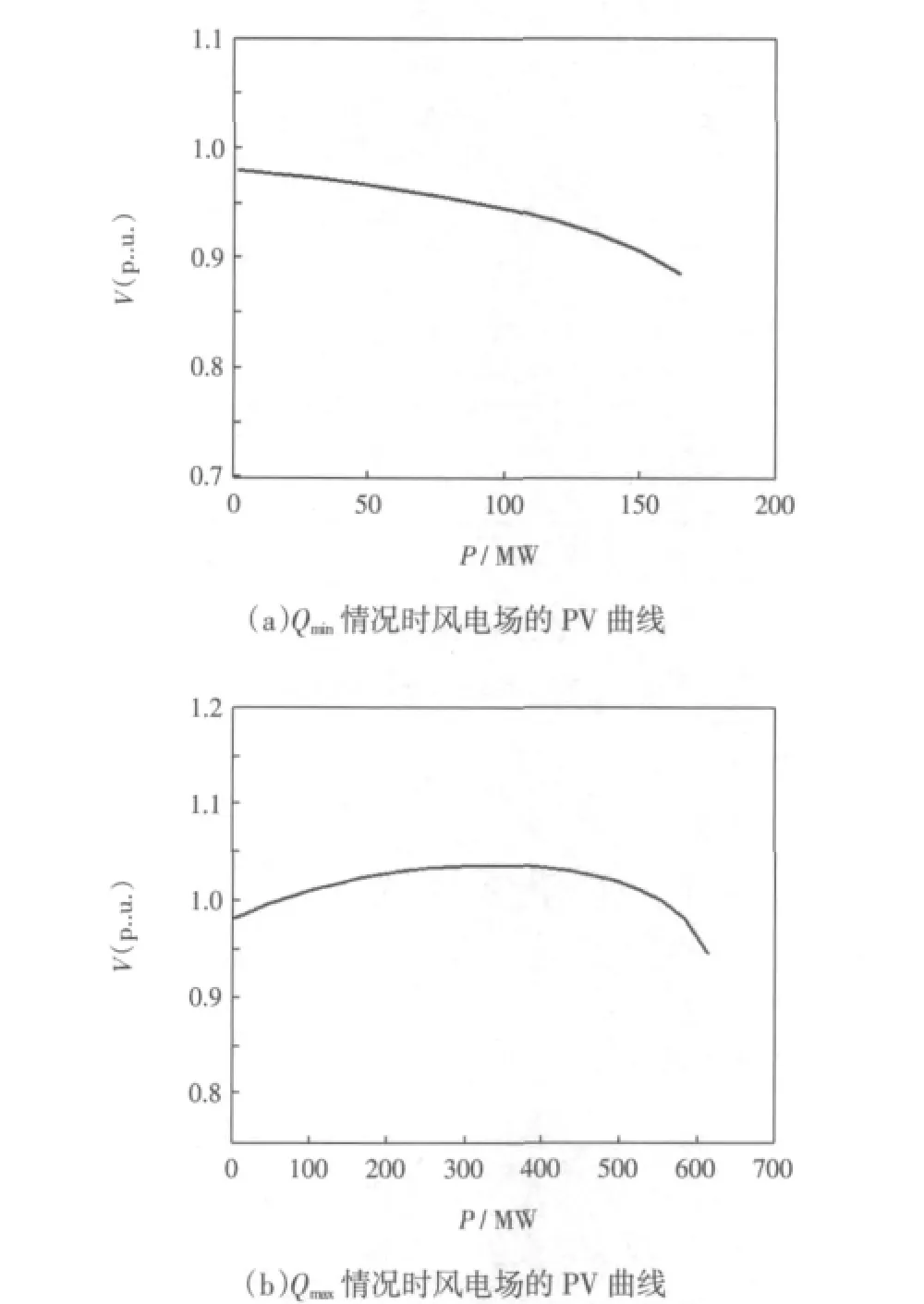
圖7 無功極限情況時風電場的PV曲線Fig.7 PV curvs of wind farm when Qmaxand Qmin

在考慮DFIG風機無功極限的情況下，其風電場的裕度值，如表1所示。

表1 考慮DFIG無功限制下風電機組接入系統的裕度情況Tab.1 Margin conditions of wind generator access to system considering the available reative power output of DFIGMW

由表1可知，DFIG無功出力不同對風電機組接入系統的穩定裕度的影響不同。當運行在無功出力下限時，風電機組接入系統的穩定裕度較小，當運行在無功出力上限時，風電機組接入系統的穩定裕度較大。這是因為DFIG機組具有無功控制能力，其提供的無功能夠支撐系統并網點電壓，有利于改善系統的靜態電壓穩定性，增大裕度。

4.3 基于分岔理論的考慮DFIG風機無功功率極限限制的風機PV曲線分析

下面討論基于分岔理論，考慮DFIG風機無功極限的風電場裕度值，分別進行仿真分析。仿真系統參數同上。取風電場母線的最低限制電壓[12]Vs=0.9（p.u.），風電場運行在 Qmin、Qmax情況時，對風場并網點母線電壓PV曲線進行分岔分析，如圖8所示。

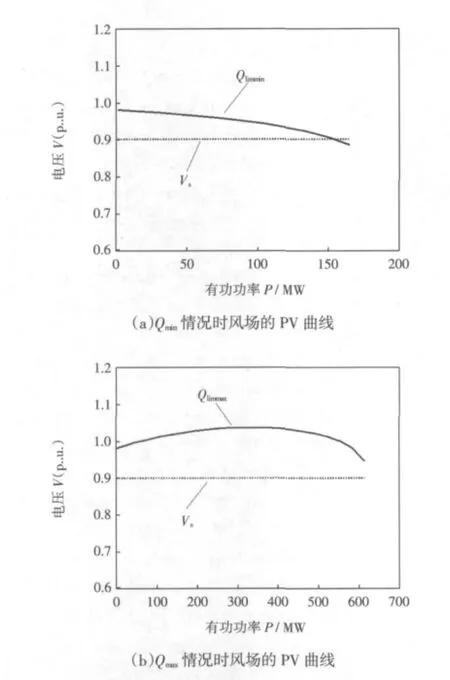
圖8 無功極限情況時風場的PV曲線Fig.8 PV curves of wind farm when Qmaxand Qmin

由圖8可見，對于Qmin的情況，風機發生了鞍結點分岔導致了系統電壓失穩。對Qmax的情況，2者沒有交點，這是由于仿真軟件和算法未呈現出曲線的下半段，但實際DFIG風機的最大無功限制曲線應和Vs相交于曲線下半段，根據圖3原理分析可知是由于風機發生極限誘導分岔導致了電壓失穩。

考慮無功極限分岔時，不同無功出力時風機的裕度值不同。對Qmin的情況，風機接入系統的穩定裕度并未改變，仍為168.0 MW，但是對于Qmax情況，由于發生LIB分岔其裕度值應小于正常的605.2 MW。

考慮風電場母線的最低限制電壓不同時的情況，當為 Vs=0.95（p.u.）時，對 Qmin、Qmax情況，進行分岔分析，如圖9所示。

圖9所示，由3.1所示的鞍結分岔定義可知，對于Qmin和Qmax的情況，風機均發生鞍結點分岔導致了系統電壓穩定性失穩。

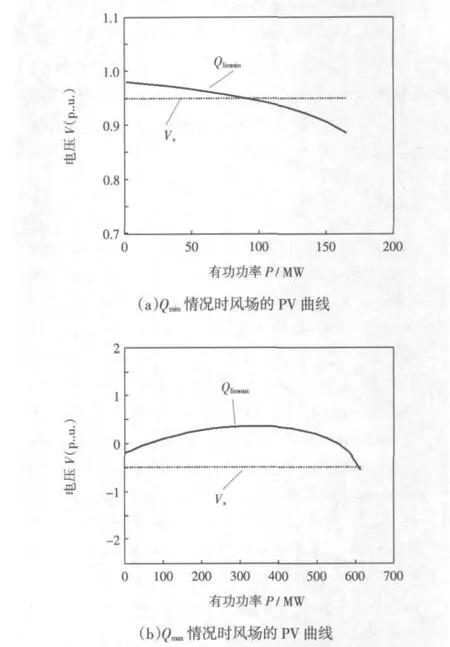
圖9 無功極限情況時風場的PV曲線Fig.9 PV curvs of wind farm when Qmaxand Qmin

由仿真結果可知，在Vs=0.95（p.u.）時裕度值與表1相同。DFIG的無功極限下系統的分岔類型不同，即造成風電失穩的起因不同，對風電接入系統的裕度影響不同。考慮DFIG發生的不同分岔可以更真實揭示系統的失穩原因和提供實際裕度。

5 結論

（1）DFIG無功出力不同對風電機組接入系統的穩定裕度的影響不同。對于DFIG運行在Qmin時，隨著風電場注入功率的增加，引起了并網點電壓下降。反之，對于Qmax情況，風電場功率增加引起了并網點電壓的升高。說明DFIG風電場的無功對系統并網節點的電壓有著重要的影響，DFIG的無功出力運行方式不可忽略。

（2）當運行在無功出力下限時，風電機組接入系統的穩定裕度較小，當運行在無功出力上限時，風電機組接入系統的穩定裕度較大。這是因為DFIG機組具有無功控制能力，其提供的無功能夠支撐系統并網點電壓，有利于改善系統的靜態電壓穩定性，增大裕度。

（3）DFIG考慮功率極限對電壓穩定裕度有一定的影響且影響分岔類型。DFIG的無功極限下系統的分岔類型不同，即造成風電失穩的起因不同，對風電接入系統的裕度影響不同。考慮DFIG發生的不同分岔可以更真實揭示系統的失穩原因和提供實際裕度。

[1]馬幼捷，楊海珊，周雪松，等（Ma Youjie，Yang Haishan，Zhou Xuesong，et al）.風電系統的電壓穩定性分析（Voltage stability analysis of wind power system）[J].電 力系統及其自動化學報（Proceedings of the CSU-EPSA），2010，22（3）：22-26.

[2]馬幼捷，張繼東，周雪松，等（Ma Youjie，Zhang Jidong，Zhou Xuesong，et al）.含風電電力系統電壓穩定問題的分岔（Bifurcation of steady state voltage stability with wind power system）[J].電 力 系 統 及 其 自 動 化 學 報（Proceedings of the CSU-EPSA），2008，20（5）：117-123.

[3]張義斌，王偉勝，戴慧珠（Zhang Yibin，Wang Weisheng，Dai Huizhu）.基于P-V曲線的風電場接入系統穩態分析（P-V curve based static analysis for integration of wind farm into power system）[J].電網技術 （Power System Technology），2004，28（23）：61-65.

[4]李作紅（Li Zuohong）.風電場接入系統靜態電壓穩定研究（Static voltage stability issues for grid integration with large-scaled wind farms）[J].電網與清潔能源（Power System and Clean Energy），2010，26（10）：53-61.

[5]張瑞明，張新燕（Zhang Ruiming，Zhang Xinyan）.基于普通異步發電機和雙饋風力發電機靜態數學模型的系統靜態電壓穩定性研究（Study on static voltage stability of power system based on static models of common and doubly fed asynchronous generators）[J].電網技術（Power System Technology），2011，35（1）：175-179.

[6]Lei Yazhou，Mullane Alan，Lightbody Gordon，et al.Modeling of the wind turbine with a doubly fed induction generator for grid integration studies[J].IEEE Trans on Energy Conversion，2006，21（1）：257-264.

[7]嚴干貴，王茂春，穆鋼，等（Yan Gangui，Wang Maochun，Mu Gang，et al）.雙饋異步風力發電機組聯網運行建模及其無功靜態調節能力研究（Modeling of grid-connected doubly-fed induction generator for reactive power static regulation capacity study）[J].電工技術學報（Transactions of China Electrotechnical Society），2008，23（7）：98-104.

[8]李華強，劉亞梅，Yorino N （Li Huaqiang，Liu Yamei，Yorino N）.鞍結分岔與極限誘導分岔的電壓穩定性評估（Voltage stability assessment for saddle node bifurcation and limit induced bifurcation）[J].中國電機工程學報（Proceedings of the CSEE），2005，25（24）：56-60.

[9]Milano F.PSAT，Matlab-based power syttem analysis toolbox[EB/OL].http：//www.uclm.es/area/gsee/Web/Federico，2007.

[10]Alsac O，Stott B.Optimal load flow with steady-state security[J].IEEE Trans on Power Apparatus and Systems，1974，93（3）：745-751.

[11]申洪（Shen Hong）.變速恒頻風電機組并網運行模型研究及其應用（Studies on Integrated Variable-Speed Constant-Frequency Wind Turbine Models and the Application） [D].北京：中國電力科學研究院（Beijing：China Electric Power Research Institute），2003.

[12]許珊珊，湯放奇，周任軍，等（Xu Shanshan，Tang Fangqi，Zhou Renjun，et al）.不同風電系統動態電壓穩定的分岔分析（Bifurcation analysis on dynamic voltage stability of power grid connected with different wind power systems）[J].電網技術（Power System Technology），2010，34（5）：67-71.