半環上保持矩陣{1}-逆的線性算子
李棟梁,任苗苗,劉建華,李斌
(1.西北大學數學系,陜西西安 710127;2.陜西廣播電視大學工程管理教學部,陜西西安 710068)
半環上保持矩陣{1}-逆的線性算子
李棟梁1,任苗苗1,劉建華1,李斌2
(1.西北大學數學系,陜西西安 710127;2.陜西廣播電視大學工程管理教學部,陜西西安 710068)
刻畫了某類特殊可換無零因子反環上保持矩陣{1}-逆的可逆線性算子,并將此結果推廣到此類無零因子反環的任意直積上.推廣了某些文獻的一些結果.
可換無零因子反環;{1}-逆;線性算子
1 引言和預備知識
設(S,+,·,0,1)是一個(2,2,0,0)-型代數,其中+和·是二元運算.且S滿足條件:
(1)(S,+,0)是一個可換含幺半群;
(2)(S,·,1)是一個含幺半群;
(3)a·(b+c)=a·b+a·c,(a+b)·c=a·c+b·c(?a,b,c∈S);
(4)0·a=a·0=0(?a∈S);
(5)0/=1,
則稱S是半環.
設S是半環,Mn(S)是指S上n階矩陣的全體,I是n階單位矩陣,O是n階零矩陣. Mn(S)上的+和·定義如下:

易證(Mn(S),+,·,O,I)是半環[1].
設A,B∈Mn(S),如果ABA=A,那么稱B是A的一個{1}-逆[2].設φ是Mn(S)上的一個算子.若對任意A,B∈Mn(S),B是A的一個{1}-逆蘊涵著φ(B)是φ(A)的一個{1}-逆,則稱φ保持矩陣{1}-逆.
線性保持問題(簡稱LPP)是近百年來矩陣論中最活躍的課題之一.它主要刻畫矩陣空間上保持映射、關系、子集等不變量的線性算子.1897年,文獻[3]刻畫了保持行列式的線性變換.起初這類問題的研究并未引起足夠的重視.直到1971年,文獻[4]發表了保持矩陣秩1的線性算子的文章之后,線性保持問題越來越受關注[1-3,5-12].隨著它在微分幾何、圖論、計算機、量子力學、控制論、經濟學等方面的廣泛應用,人們更加認識到研究線性保持問題的重要性.
近年來一些學者研究了域、環和半環上保持矩陣{1}-逆的線性算子.文獻[5-6]討論了保持特征為2的主理想整環上矩陣{1}-逆的線性算子.文獻[13]刻畫了保持特征不為2的域上矩陣{1}-逆的加法算子.文獻[11]研究了保持兩類特殊半環上矩陣上{1}-逆的線性算子.在文獻[11]的基礎上,本文將刻畫一類特殊無零因子反環上保持矩陣{1}-逆的可逆線性算子.
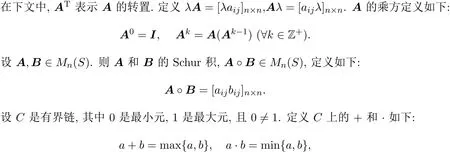
則(C,+,·,0,1)成為半環,稱其為鏈半環.易見,鏈半環一定是可換無零因子反環.
設P是實數環?(在普通的加法和乘法下)的含幺子環,P的非負部分記為P+.容易驗證,P+是半環.非負整數半環Z+和非負實數半環?+都是P+的例子.顯然,Z+和?+是可換無零因子反環.

則(B1,+,·)成為半環.稱其為二元布爾代數[1].
設S是半環,若(S,·,1)是可換的,則稱S是可換的.若對任意a,b∈S,a+b=0蘊涵著a=b=0,則稱S是反環[10].若對任意a,b∈S,ab=0蘊涵著a=0或b=0,則稱S是無零因子的.
設φ是Mn(S)上的算子,若φ滿足對任意A,B∈Mn(S),a,b∈S有
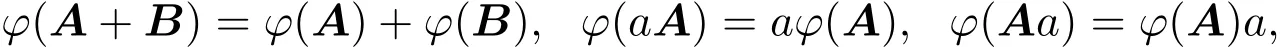
則稱φ是Mn(S)上的線性算子.
Ei,j∈Mn(S)表示在(i,j)位置為1,其余位置為0的矩陣.對于矩陣P∈Mn(S),如果P的每一行和每一列都只有一個非零元,且非零元是1,那么稱P是一個排列矩陣.需要注意的是若P∈Mn(S)是排列矩陣,則PPT=PTP=I.

2 主要結果
引理2.1[11]S是可換無零因子反環,φ是Mn(S)上的線性算子.若φ是保持矩陣{1}-逆的可逆線性算子,則存在P,B∈Mn(S)使得
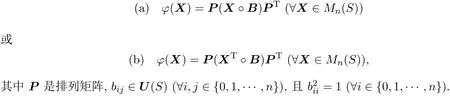
定理2.1設S是可換無零因子反環,滿足條件:對于任意的a∈S,a2=1蘊涵著a=1.φ是Mn(S)上的線性算子,則φ是保持矩陣{1}-逆的可逆線性算子的充分必要條件是存在可逆矩陣U∈Mn(S),使得

進一步,bijbji=1.
下面討論n≥3的情形.對互不相等的i,j,k∈n,由

其中D=diag{b11,b21,…,bn1}.設U=PD.易見,U是可逆的.故φ(X)=P(X?B)PT= UXU-1.當n≤2時,容易得到結論仍是成立的.
類似可證φ(X)=P(XT?B)PT的情形.
(?=)當φ(X)=UXU-1時,易驗證φ是可逆的.對任意A,B∈Mn(S),若A=ABA, 則

故φ是保持矩陣{1}-逆的.類似可證φ(X)=UXTU-1的情形.
當S=B1,?+,Z+,或C時,S滿足定理2.1的條件,故文獻[11]中的推論2.3和2.6可由定理2.1得到.
引理2.2[12]設S=∏λ∈∧Sλ,其中(?λ∈∧)Sλ是半環.設φ是Mn(S)上的線性算子. 則φ保持矩陣{1}-逆當且僅當對于任意的λ∈∧,φλ保持矩陣{1}-逆.
定理2.3設S=∏λ∈∧Sλ,其中(?λ∈∧)Sλ是可換無零因子反環,滿足條件:對于任意的a∈Sλ,a2=1蘊涵著a=1.設φ是Mn(S)上的線性算子.則φ是保持矩陣{1}-逆的線性算子當且僅當存在可逆矩陣U∈Mn(S)和f1,f2∈S使得

其中U是可逆矩陣,(f1)λ,(f2)λ∈{0,1},(f1)λ/=(f2)λ(?λ∈∧).
證明(=?)由引理1.1和引理2.2知對于任意的λ∈∧,φλ是保持矩陣{1}-逆的可逆線性算子.又由定理2.1知存在可逆矩陣U使得
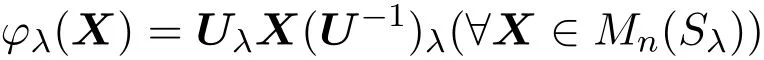

由定理2.1知φλ是保持矩陣{1}-逆的可逆的線性算子.又由引理1.1得φ是保持矩陣{1}-逆的可逆的線性算子.
易見,文獻[12]中的推論2.3.1和推論2.3.2是定理2.2的特殊情形.
致謝作者衷心感謝趙憲鐘教授的悉心指導.
[1]Song S Z,Kang K T,Beasley L B.Idempotent matrix preservers over Boolean algebras[J].J.Korean Math. Soc.,2007,44(1):169-178.
[2]Rao P S S N V P,Rao K P S B.On generalized inverses of Boolean matrices[J].Linear Algebra Appl., 1975,11:135-153.
[3]Frobenius G.Uber Die Drastellung Der Endlichen Grouppen Durch Lineare Substitutionen[M].Berlin: Sitzungsber.Preuss.Akad.Wiss.,1897.
[4]Marcus M.Linear transformations on matrices[J].J.Res.Nat.Bur.Standards,1971,75B:107-113.
[5]卜長江,郝立麗.保矩陣{1}逆的線性映射[J].數學研究,2003,36(4):418-421.
[6]Bu C J.Invertible linear maps preserving{1}-inverses of matrices over PID[J].J.Appl.Math.Computing, 2006,22(3):255-265.
[7]Chan C H,Lim M H.Linear transformations on symmetric matrices that preserve commutativity[J].Linear Algebra Appl.,1982,47:11-22.
[8]Chan G H,Lim M H,Tan K K.Linear preservers on matrices[J].Linear Algebra Appl.,1987,93:67-80.
[9]Choi M D,Jafarian A A,Radjavi H.Linear maps preserving commutativity[J].Linear Algebra Appl., 1976,87:227-241.
[10]DolˇZan D,Oblak P.Idempotent matrices over antirings[J].Linear Algebra Appl.,2009,431(5/6/7):823-832.
[11]任苗苗,邵勇,趙憲鐘.保持半環上矩陣{1}-逆的線性算子[J].西北大學學報:自然科學版,2012,42(1):7-11.
[12]任苗苗.幾類保持半環上矩陣不變量的線性算子[D].西安:西北大學數學系,2012.
[13]張顯,曹重光.關于域上矩陣廣義逆的加法映射[J].數學學報,2004,47(5):1013-1018.
Linear operators preserving{1}-inverses of matrices over semirings
Li Dongliang1,Ren Miaomiao1,Liu Jianhua1,Li Bin2
(1.Department of Mathematics,Northwest University,Xi′an 710127,China; 2.Department of Project Management,Shaanxi Radio and TV University,Xi′an 710068,China)
In this paper we characterize invertible linear operarors that preserve{1}-inverses of matrices over special entire antirings.Based on obtained results,we give forms of invertible linear operarors that preserve {1}-inverses of matrices over direct product of special entire antirings.Thus some results obtained in some essays are generalized.
commutative entire antiring,{1}-inverse,linear operator
O152.7
A
1008-5513(2013)02-0185-05
10.3969/j.issn.1008-5513.2013.02.012
2013-01-17.
陜西省自然科學專項基金(2011JQ1017).
李棟梁(1986-),碩士生,研究方向:代數學.
2010 MSC:15A04,15A86,16Y60

