兩個變系數非線性Schr?dinger 的精確解

黃彥輝，張金良，魏鵬波

(河南科技大學數學與統計學院，河南洛陽471023)

0 引言

變系數非線性Schr?dinger 方程

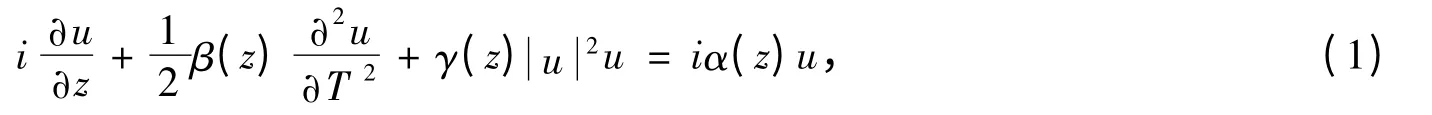
當考慮到色散系數、非線性參數和增益系數為z 函數時，方程(1)是光通訊中非常重要的模型。文獻［1］利用變系數F-展開法導出了方程(1)的Jacobi 橢圓函數解;文獻［2］從可積的觀點，基于Lax 對得到了Darboux 變換，借助于該變換，導出了方程(1)的精確多孤子解，并由此得到了顯式單孤子解和二孤子解。文獻［3］先預設解形式，直接代入方程(1)，得到方程的顯式精確解;文獻［4］利用變分法，得到了方程(1)的顯式解析近似解;借助于Lie 群約化方法，文獻［5］導出了方程(1)的精確解。

本文考慮的另一個變系數非線性Schr?dinger 方程為:

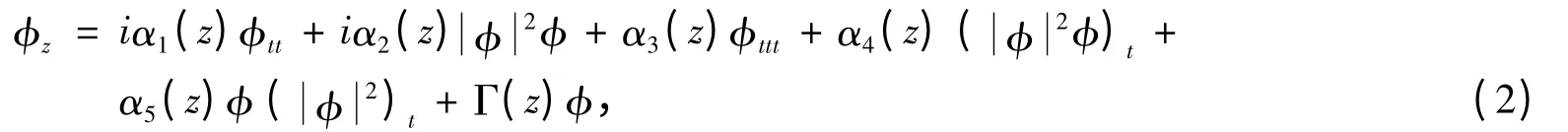
其中，φ(z，t)為電場的復包絡;α1(z)、α2(z)、α3(z)、α4(z)和α5(z)分別為二階色散、非線性Kerr 效應引起的自相位調制、自陡崤和自頻移參數;Γ(z)為增益參數。由于有著廣泛的應用，方程(2)已引起眾多學者的關注。文獻［6 -10］研究了方程(2)，得到了顯式亮孤子解、暗孤子解。文獻［11］利用擴展的tanh-展開法，在參數滿足一定的條件下得到了擬亮孤子解、暗孤子解。文獻［12］借助于輔助橢圓型方程，導出了方程(1)和方程(2)的精確解。

本文利用齊次平衡原則［13-16］及二階線性輔助常微分方程，求出輔助橢圓型方程的精確解，借助于輔助橢圓型方程，導出了兩個變系數非線性Schr?dinger 方程(1)和方程(2)的精確解。

1 輔助橢圓型方程的精確解

考慮

依據齊次平衡原則，設輔助橢圓型方程(3)的精確解形如下:

其中，d－1和d1為待定常數;G = G(ξ)滿足二階輔助常微分方程:

其中，μ 為待定常數。

將式(4)代入式(3)并利用式(5)，得方程(3)的精確解如下。

情形1 A ＞0，B ＜0。

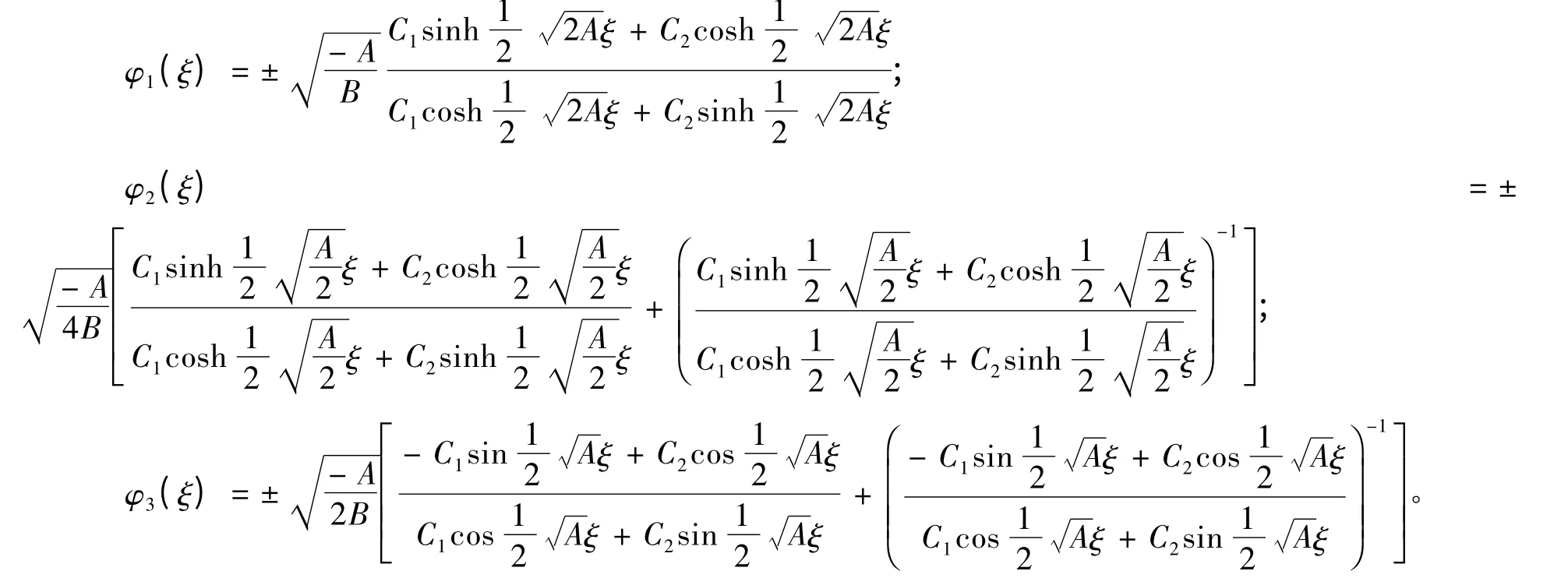
情形2 A ＜0，B ＜0。

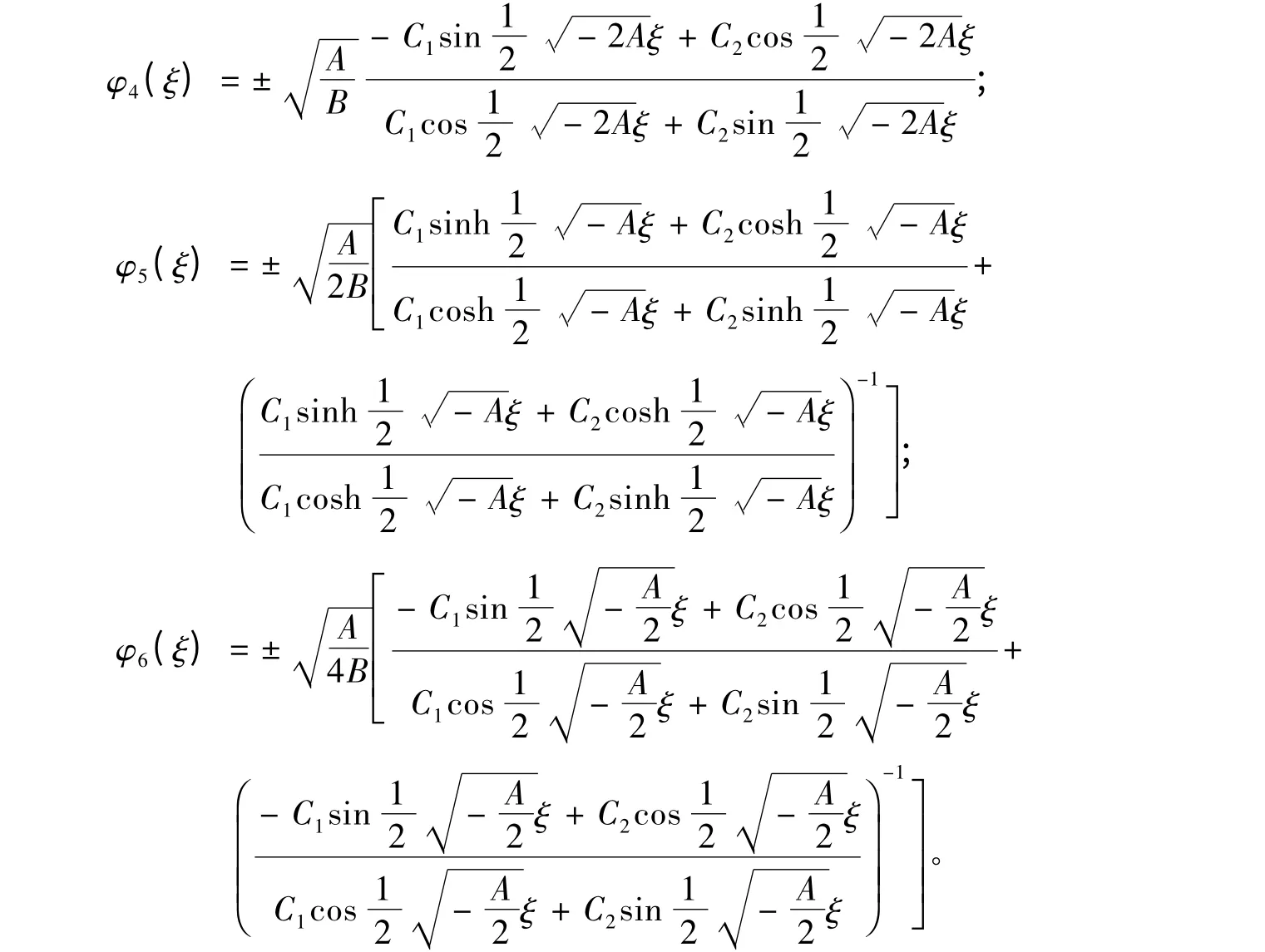
情形3 A = 0，B ＜0。

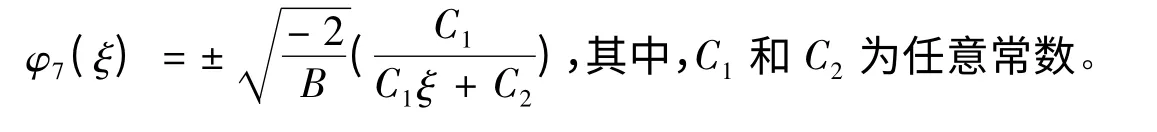
2 方程(1)和方程(2)的精確解

由文獻［12］知，方程(1)的精確解表示為:

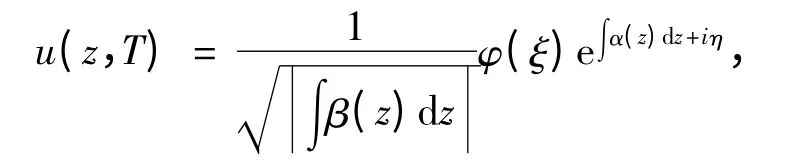
方程(1)中的系數α(z)、β(z)和γ(z)滿足

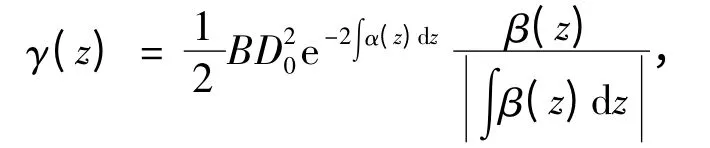
其中，D0、D1、A 和B 為常數;φ(ξ)滿足輔助方程(3)。

借助于輔助方程(3)的解，可得方程(1)的精確解，表示為:

情形1 A ＞0，B ＜0。

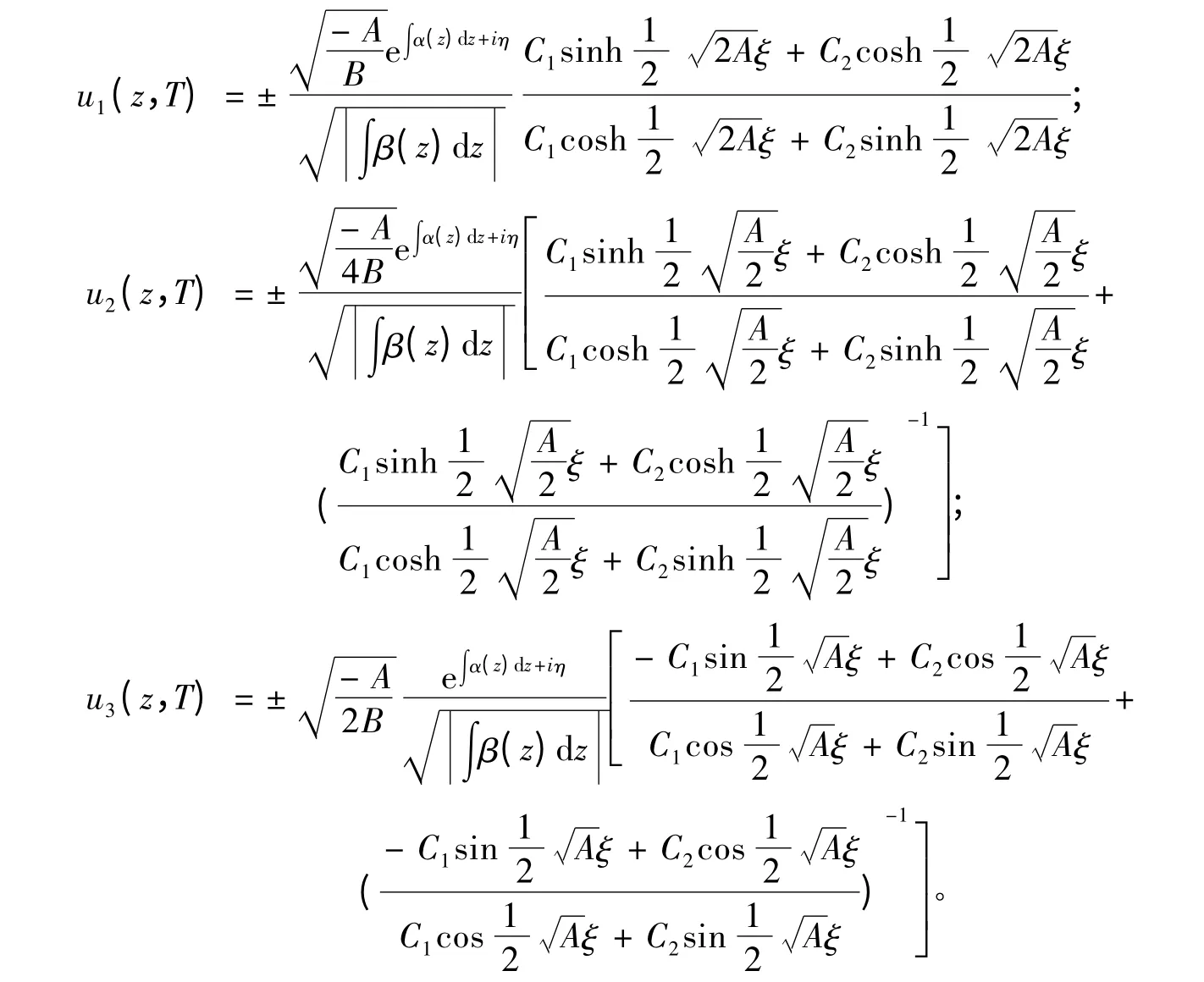
情形2 A ＜0，B ＜0。

情形3 A = 0，B ＜0。

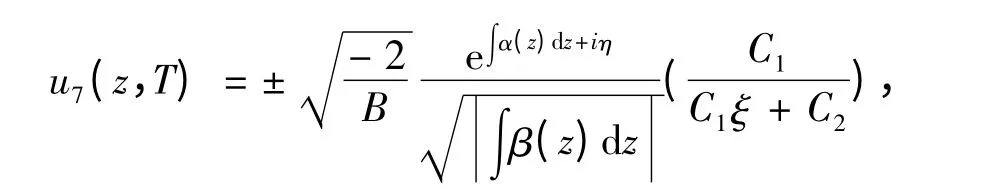
由文獻［12］知，方程(2)的精確解可分為兩種情況:(Ⅰ)α1(z)+ 3κα3(z)≠0;(Ⅱ)α1(z)+3κα3(z)= 0。

對于以上兩種情況，方程(2)的精確解可借助于輔助方程(3)的解導出，為了簡潔起見，本文不再一一列出。

3 結論與分析

本文用二階線性常微分方程導出了輔助橢圓型方程的精確解，然后，借助于該輔助橢圓型方程推導出了兩個變系數NLS 類方程的解以及相應的約束條件，和文獻［3，10］中的算法相比，本文的計算方法更簡潔、直接。

［1］ Zhang J F，Dai C Q，Yang Q，et al.Variable-coefficient F-expansion Method and Its Application to Nonlinear Schr?dinger Equation［J］.Optics Communications，2005，252:408 -421.

［2］ Hao R Y，Li L，Li Z H，et al. A New Approach to Exact Soliton Solutions and Soliton Interaction for the Nonlinear Schrodinger Equation with Variable Coefficients［J］.Optics Communications，2004，236:79 -86.

［3］ 張善卿，李志斌.一類變系數非線性Schr?dinger 方程的精確解析解［J］.華東師范大學學報，2003(2):32 -35.

［4］ Wen S C，Xu W C，Guo Q，et al.Evolution of Solitons of Nonlinear Schrodinger Equation with Variable Parameters［J］.中國科學:A 輯，1997，40:1300 -1304.

［5］ 阮航宇，陳一新.尋找變系數非線性方程精確解的新方法［J］.物理學報，2000，49(2):177 -180.

［6］ Hao R Y，Li L，Li Z H，et al. A New Way to Exact Quasi-soliton Solutions and Soliton Interaction for the Cubic-quintic Nonlinear Schr?dinger Equation with Variable Coefficients［J］.Optics Communications，2005，245(1/6):383 -390.

［7］ Yang R C，Hao R Y，Li L，et al. Dark Soliton Solution for Higher-order Nonlinear Schrodinger Equation with Variable Coefficients［J］.Optics Communications，2004，242(1/3):285 -293.

［8］ Hao R Y，Li L，Li Z H，et al. Exact Multi-Soliton Solutions of the Higher Order Nonlinear Schr?dinger Equation with Variable Coefficients［J］.Phys Rev E，2004，70:066603.

［9］ Yang R C，Li L，Hao R，et al.Combined Solitary Wave Solutions for the Inhomogeneous Higher-order Nonlinear Schrodinger Equation［J］.Phys Rev E，2005，71:036616.

［10］ Yang R C，Hao R U，Li L，et al. Dark Soliton Solution for Higher-order Nonlinear Schrodinger Equation with Variable Coefficients［J］.Optics Communications，2004，242:285 -293.

［11］ Zhang J F，Yang Q，Dai C Q. Optical Quasi-soliton Solutions for Higher-order Nonlinear Schr?dinger Equation with Variable Coefficients［J］.Optics Communications，2005，248:257 -265.

［12］ Zhang J L，Li B A，Wang M L.The Exact Solutions and the Relevant Constraint Conditions for Two Nonlinear Schr?dinger Equations with Variable Coefficients［J］.Chaos，Solitons and Fractal，2009，39:858 -865.

［13］ Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations［J］.Physics Letters A，1995，199:169 -172.

［14］ Wang M L，Zhou Y B，Li Z B.Application of a Homogeneous Balance Method to Exact Solutions of Nonlinear Equations in Mathematical Physics［J］.Physics Letters A，1996，216:67 -75.

［15］ Zhang J L，Wang Y M，Wang M L，et al.New Application of the Homogeneous Balance Principle［J］.Chinese Physics，2003，12:245 -250.

［16］ 王明亮，李志斌，周宇斌.齊次平衡原則及其應用［J］.蘭州大學學報，1999，35(3):8 -16.