CW-PSO及其在古建筑傳感器優(yōu)化配置中的應(yīng)用研究

路 楊，張曉麗

1.河南大學(xué) 計算中心，河南 開封 4750002.河南大學(xué) 計算機與信息工程學(xué)院，河南 開封 475000

CW-PSO及其在古建筑傳感器優(yōu)化配置中的應(yīng)用研究

路 楊1，張曉麗2

1.河南大學(xué) 計算中心，河南 開封 475000
2.河南大學(xué) 計算機與信息工程學(xué)院，河南 開封 475000

1 引言

近幾年來，在文物保護方面，木構(gòu)古建筑本體及其環(huán)境的監(jiān)測顯得越來越重要。通過對木構(gòu)古建筑進行監(jiān)測，可以為文物建筑的維護方案提供可靠和必要的數(shù)據(jù)。環(huán)境監(jiān)測是建筑結(jié)構(gòu)健康監(jiān)測的重要部分，傳感器優(yōu)化配置是健康監(jiān)測的基礎(chǔ)。如何將有限數(shù)量的傳感器布置在合適的節(jié)點上并獲得較為全面的信息是目前健康監(jiān)測領(lǐng)域研究的熱點之一。

粒子群優(yōu)化算法（PSO）是一種基于群智能的全局優(yōu)化方法[1-2]，它源于對鳥群覓食運動行為的模擬。目前已廣泛應(yīng)用于函數(shù)優(yōu)化[3-4]、神經(jīng)網(wǎng)絡(luò)訓(xùn)練[5]、組合優(yōu)化[6-7]、模式分類和模糊控制以及工程應(yīng)用[8-9]等領(lǐng)域。但是它存在局部搜索能力較差，搜索精度不高并且容易早熟等問題。為了提高算法的性能，研究者在PSO算法的參數(shù)以及與其他算法相結(jié)合方面做了很多研究[10-11]。

2 標準粒子群算法描述

粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）是Kennedy和Eberhart于1995年提出的一種基于種群搜索策略的全局優(yōu)化進化算法，它模擬鳥類的覓食行為，通過個體間的協(xié)作和競爭實現(xiàn)最優(yōu)解的搜索。在求解優(yōu)化問題時，算法首先初始化產(chǎn)生一群隨機粒子，在解決實際問題中粒子代表問題的一個可能解。粒子群優(yōu)化算法是基于群體和適應(yīng)度的，在迭代過程中，通過粒子的適應(yīng)度函數(shù)值來評價粒子的優(yōu)劣。每個粒子具有位置和速度兩個特征，假設(shè)粒子在D維的目標搜索空間中飛行，那么第i個粒子的位置表示為：

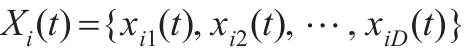
第i個粒子的速度表示為：

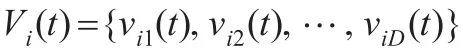
粒子當(dāng)前搜索到的最優(yōu)值稱為個體極值，當(dāng)前群體最優(yōu)稱為全局極值。在每次迭代過程中，粒子通過跟蹤個體極值和當(dāng)前粒子群找到的最優(yōu)解即全局極值來更新自己的速度和位置，從而搜尋到問題的最優(yōu)解。粒子的速度與位置更新公式如下：

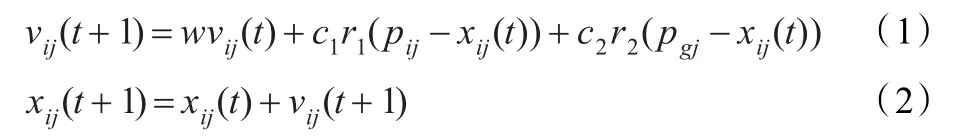
在式（1）和式（2）中，1≤j≤D，w為慣性權(quán)重，學(xué)習(xí)因子c1、c2是非負常數(shù)，通常取值為2；vij(t)∈[-vmax，vmax]；r1和r2是介于[0，1]之間的隨機數(shù)；vmax是常數(shù)，由用戶設(shè)定。

3 基于余弦自適應(yīng)調(diào)整慣性權(quán)重的粒子群優(yōu)化算法（CW-PSO）

3.1 種群聚集度

種群聚集度反映了所有粒子當(dāng)前的聚集程度[12]，聚集度s如式（3）所示。

其中 favg(t)是第t代中所有粒子的平均適應(yīng)度值，fg(t)是第t代粒子群中最優(yōu)粒子的適應(yīng)度值。其中0＜s≤1，反映了所有粒子當(dāng)前的聚集程度，s越小，說明粒子群中所有的粒子越分散，s越大，粒子越聚集。

3.2 余弦自適應(yīng)調(diào)整慣性權(quán)重策略

慣性權(quán)重w在粒子群優(yōu)化算法中起著至關(guān)重要的作用，控制著PSO的全局與局部搜索能力。w值越大，全局搜索能力越強，有利于跳出局部極值；反之，局部開發(fā)能力越強，越容易收斂[13]。在標準粒子群算法中，Shi Y等人[14]采取線性遞減慣性權(quán)重策略（LDW），即w從0.9到0.4線性下降，使得PSO在搜索初期快速尋找到全局最優(yōu)解，隨著w逐漸減小，粒子速度變慢，開始精細的局部搜索。研究者又相繼提出了模糊調(diào)整慣性權(quán)重策略、隨機調(diào)整慣性權(quán)重策略等，研究表明這些調(diào)整策略能有效避免粒子群的早熟收斂，優(yōu)化結(jié)果精度較高。

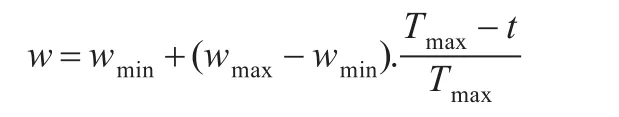
文獻[15]提出基于步長較小的慣性權(quán)重線性遞減策略（SL-PSO），步長較小，w的變化幅度較小，粒子群不易陷入局部最優(yōu)。但是由于線性遞減慣性權(quán)重策略普遍存在不能很好地平衡全局和局部搜索能力的缺點。為了彌補線性遞減慣性權(quán)重策略的不足，本文對文獻[15]中的慣性權(quán)重進行修正，在其基礎(chǔ)上提出了基于余弦自適應(yīng)調(diào)整慣性權(quán)重的粒子群優(yōu)化算法（CW-PSO），并引入種群聚集度的概念。w的修正策略如下：

（1）當(dāng)0＜s≤1時，粒子的位置分布比較分散，以步長21/T2max非線性遞減。由式（4）可以看出，步長較小，w的減小速度緩慢，維護了群體的多樣性，有利于全局搜索，從而避免了算法的早熟收斂。

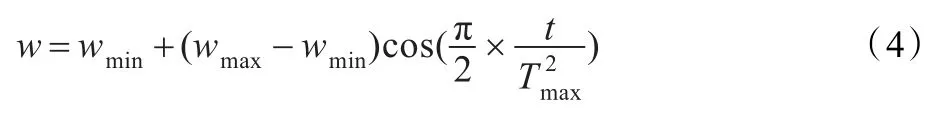
（2）當(dāng)1＜s≤1時，此時粒子的位置相對比較集中，以

2步長1/Tmax非線性遞減，相比式（4），步長增大，w的減小趨勢加快。由于余弦函數(shù)的特點，避免了粒子群體的多樣性迅速降低。與SL-PSO算法相比，CW-PSO算法更易進行精細的局部搜索，提高了算法的精度。

在式（4）、式（5）中wmax為最大慣性權(quán)重，wmin為最小慣性權(quán)重，Tmax為終止迭代次數(shù)，t為當(dāng)前進化代數(shù)。

4 基于CW-PSO的傳感器優(yōu)化配置

設(shè)n個溫度傳感器所在節(jié)點的位置為x1，x2，…，xn，并按從1到n編碼，在某時刻每個溫度傳感器測得的溫度觀測值為T1，T2，…，Tn。在建筑物結(jié)構(gòu)上布置傳感器，為了減少傳感器的數(shù)量，在保證能獲得較為全面的溫度信息的前提下，盡可能選擇在溫差較大的節(jié)點上布置傳感器。假設(shè)共有n個節(jié)點，傳感器的預(yù)算個數(shù)為 p，則S表示為粒子位置對應(yīng)的 p個傳感器節(jié)點的集合，這 p個整數(shù)均介于1 到n之間且互不相等。在本文中，問題解的優(yōu)化目標函數(shù)如式（6）所示，粒子群優(yōu)化的目的是為了使 f最大化。其中k≠i，i?S，由于溫度傳感器是實時監(jiān)測的，為了簡化適應(yīng)度函數(shù)，本文設(shè)定Ti是在一個節(jié)點i上某月的平均溫度。

5 仿真實驗

選取建筑物結(jié)構(gòu)的20個節(jié)點，按從1到20進行編碼。經(jīng)測量統(tǒng)計，每個節(jié)點在2007年11月份測得的平均溫度如表1所示。

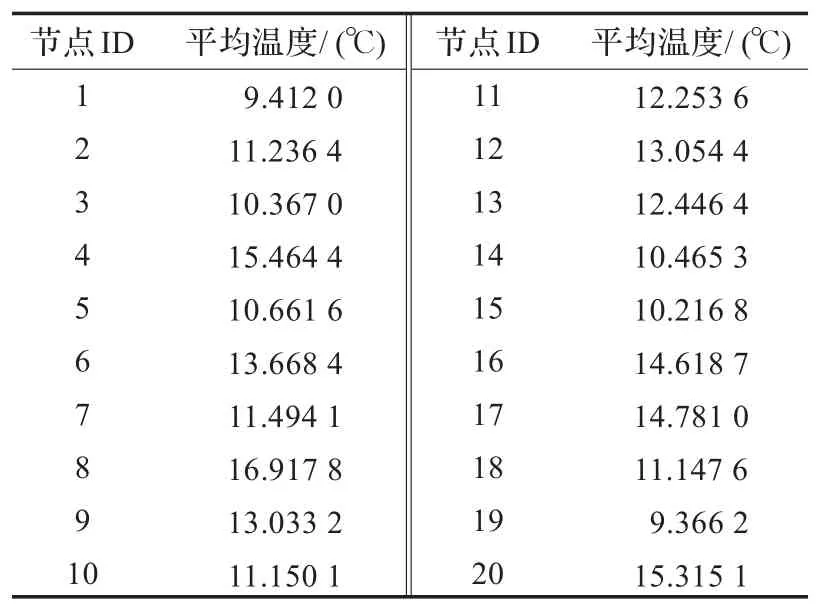
表1 節(jié)點與平均溫度

按照粒子群算法的流程，用MATLAB仿真工具編制了程序。取粒子數(shù)M=10，傳感器預(yù)算數(shù)目P，wmax=0.9，wmin=0.4。本文用式（6）的適應(yīng)度函數(shù)測試CW-PSO算法的性能，并與線性遞減慣性權(quán)重粒子群算法（LDW）、基于步長的線性遞減策略粒子群優(yōu)化算法（SL-PSO）進行比較。三種粒子群算法所取參數(shù)均和上述參數(shù)相同。為了使結(jié)果更加精確，分別設(shè)置Tmax為200、300，每個算法獨立運行20次。測試結(jié)果如表2和表3所示。

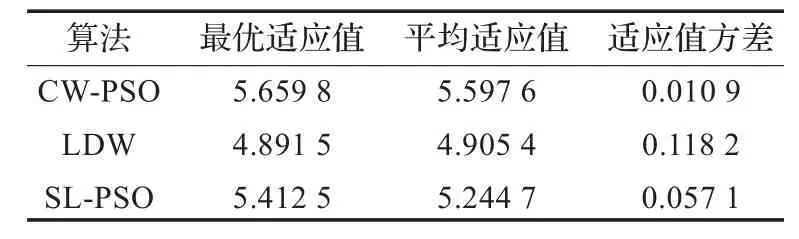
表2 算法的測試性能仿真（Tmax=300）

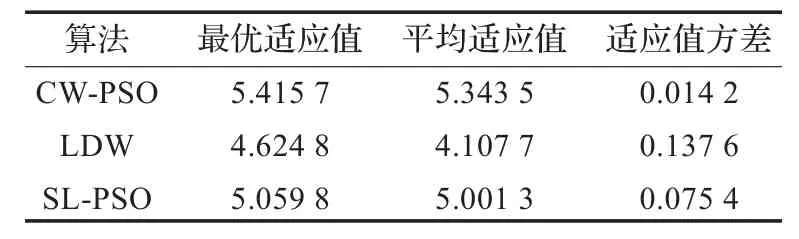
表3 算法的測試性能仿真（Tmax=200）

當(dāng)Tmax為300時，由圖1可以看出，隨著傳感器數(shù)量的增加，粒子的適應(yīng)度函數(shù)值也在增加，但傳感器數(shù)量從9以后，適應(yīng)值遞增梯度非常小，故傳感器數(shù)量可選9。程序運行后CW-PSO算法輸出的粒子全局最優(yōu)位置為（1，2，4，5，7，8，12，17，20），最優(yōu)值為5.659 8。由圖2可以看出線性遞減慣性權(quán)重算法（LDW）收斂速度過慢；SL-PSO算法采用基于步長較小的線性遞減慣性權(quán)重策略，提高了搜索速度和收斂精度；CW-PSO算法迭代速度稍慢于SL-PSO算法，由于群體的多樣性高，避免了算法過早地收斂以及陷入局部最優(yōu)，并且能夠很好地平衡全局搜索和局部搜索能力。

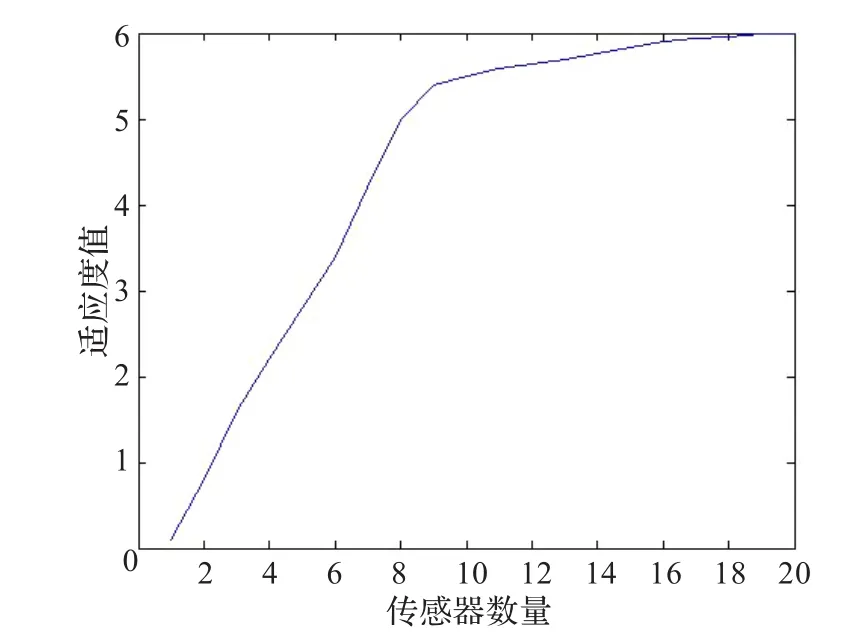
圖1 適應(yīng)度函數(shù)值隨傳感器數(shù)量變化曲線圖

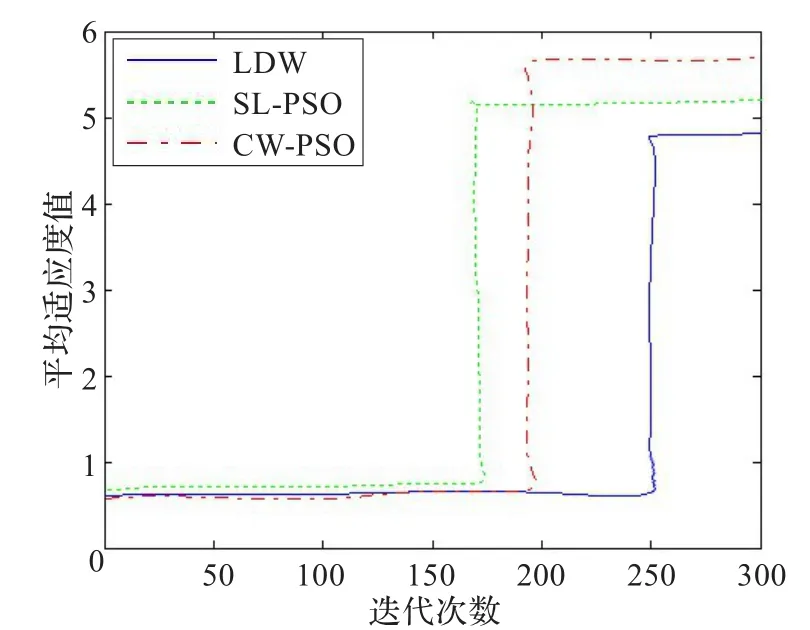
圖2 三種算法的適應(yīng)度迭代曲線圖

6 結(jié)束語

針對粒子群優(yōu)化算法存在早熟收斂以及不能較好地控制其在全局和局部搜索的平衡性等缺點，在分析慣性權(quán)重對算法性能影響的基礎(chǔ)上提出了基于余弦自適應(yīng)調(diào)整慣性權(quán)重的粒子群優(yōu)化算法，并引入種群聚集度概念，然后采用該算法對木構(gòu)古建筑傳感器配置進行優(yōu)化。在粒子群分布比較分散時，粒子群收斂速度快，迭代曲線平穩(wěn)，全局搜索能力強；當(dāng)粒子的位置比較集中時，粒子的速度相對比較緩慢，在局部范圍內(nèi)尋優(yōu)能力強。經(jīng)仿真分析，算法的性能有了明顯的提高，并且驗證了用粒子群優(yōu)化算法求解傳感器優(yōu)化配置問題的可行性。

[1]Eberhart R C，Kennedy J.A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science.Piscataway NJ：IEEE Service Center，1995：39-43.

[2]Kennedy J，Eberhart R C.Particle swarm optimization[C]// Proc IEEE International Conference on Neural Networks. Piscataway NJ：IEEE Service Center，1995：1942-1948.

[3]He Q，Wang L.An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J]. Engineering Applications of Artificial Intelligence，2007，120 （4）：89-99.

[4]Wang Y J，Yang Y P.Particle swarm optimization with preference orderranking formulti-objective optimization[J]. Information Sciences，2009，179（12）.

[5]高海兵，高亮，周馳，等.基于粒子群優(yōu)化的神經(jīng)網(wǎng)絡(luò)訓(xùn)練算法研究[J].電子學(xué)報，2004，32（9）：1572-1574.

[6]沈顯君，王偉斌，鄭波盡，等.基于改進的微粒群優(yōu)化算法的0-1背包問題求解[J].計算機工程，2006，32（18）：23-24.

[7]Tchomte S K.Particle swarm optimization：a study of particle displacement for solving continuous and combinatorialoptimization problems[J].Int J Production Economics，2009，12（9）：108-110.

[8]王旸，劉曉東，徐小慧，等.基于粒子群優(yōu)化的數(shù)據(jù)分類算法[J].系統(tǒng)仿真學(xué)報，2008，20（22）：6158-6162.

[9]王曉敏，劉希玉，戴芬.基于PSO的關(guān)聯(lián)規(guī)則挖掘方法及應(yīng)用[J].信息技術(shù)與信息化，2009（3）：85-87.

[10]徐剛，楊玉群，黃先玖.一種非線性權(quán)重的自適應(yīng)粒子群優(yōu)化算法[J].計算機工程與應(yīng)用，2010，46（35）：49-51.

[11]Chatterjeea A，Siarry P.Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers and Operations Research，2006，34（4）：859-871.

[12]王潤芳，張耀軍，裴志松.新型的動態(tài)粒子群優(yōu)化算法[J].計算機工程與應(yīng)用，2011，47（16）：32-34.

[13]田野.粒子群優(yōu)化算法及其應(yīng)用研究[D].長春：吉林大學(xué)，2010.

[14]Shi Y，Eberhart R C.A modified particle swarm optimizer[C]// Proceedings of the IEEE International Conference on Evolutionary Computation.Piscataway NJ：IEEE Service Center，1998：69-73.

[15]胡建秀，曾建潮.微粒群算法中慣性權(quán)重的調(diào)整策略[J].計算機工程，2007，33（11）：193-195.

LU Yang1,ZHANG Xiaoli2

1.Computing Center,Henan University,Kaifeng,Henan 475000,China
2.School of Computer and Information Engineering,Henan University,Kaifeng,Henan 475000,China

Aiming at the premature convergence problem and unbalance of global search and local search in particle swarm optimization algorithm,this paper proposes a particle swarm optimization algorithm based on cosine adaptive adjusting inertia weight.The improved particle swarm optimization is applied in optimal sensor placement of wooden historic architecture.Simulation results show that it can avoid premature convergence to an extent,improve the global search ability and obtain accurate results of optimization by simulation experiment.

particle swarm optimization algorithm;inertia weight;wooden historic architecture;optimal sensor placement

針對粒子群優(yōu)化算法容易陷入早熟收斂以及全局搜索和局部搜索平衡能力差等缺點，提出了基于余弦自適應(yīng)調(diào)整慣性權(quán)重的粒子群優(yōu)化算法（CW-PSO），并將其應(yīng)用在木構(gòu)古建筑傳感器優(yōu)化配置中。仿真結(jié)果表明，該算法在一定程度上避免了早熟收斂，提高了全局和局部搜索性能，又能得到較為精確的尋優(yōu)結(jié)果。

粒子群優(yōu)化算法；慣性權(quán)重；木構(gòu)古建筑；傳感器優(yōu)化配置

A

TP39

10.3778/j.issn.1002-8331.1209-0029

LU Yang,ZHANG Xiaoli.Particle swarm optimization based on cosine adaptive adjusting inertia weight and its application research in optimal sensor placement of historic architecture.Computer Engineering and Applications,2013,49（5）：268-270.

國家青年基金（No.61203094）；河南省科技攻關(guān)（No.122102210052）。

路楊（1972—），女，博士，副教授，主要研究方向：模式識別、數(shù)據(jù)挖掘；張曉麗（1987—），女，碩士生，主要研究方向：模式識別、數(shù)據(jù)挖掘。E-mail：kangkangxiao2006@163.com

2012-09-10

2012-12-06

1002-8331（2013）05-0268-03