最小平均等待時間約束下的備件庫存優化模型
王玉文,金家善,陳硯橋,魏曙寰
(海軍工程大學動力工程學院,湖北武漢430033)
最小平均等待時間約束下的備件庫存優化模型
王玉文,金家善,陳硯橋,魏曙寰
(海軍工程大學動力工程學院,湖北武漢430033)
應用裝備平均等待備件時間與備件的延期交貨量之間的數學關系,構建以裝備平均等待備件時間為約束條件的庫存優化模型。然后運用邊際效應分析方法描述了備件庫存優化流程。最后以算例的形式,對備件庫存量進行預測,驗證優化模型的可信性。
平均等待備件時間;延期交貨量;邊際效應;優化
0 引言
備件數量的確定是裝備綜合保障的一個重要組成部分,它直接決定裝備的戰備完好和任務的持續能力。制定科學的備件存儲模型,確定合理的備件儲備數量,既能滿足裝備的使用要求,又能大幅度降低備件的全壽命周期費用。為了確定可更換部件最優的儲備數量,需要建立備件數量與系統性能的關聯關系。目前,國內外對備件庫存模型作了大量研究。文獻[1-3]研究了備件保障概率約束下的備件數量模型。文獻[4]論述了以裝備可用度為約束條件的備件庫存優化算法。但是,這些模型并沒有建立裝備因等待備件而導致的停機時間與備件庫存量之間的關系。
在影響裝備可用度的3種主要停機時間要素中,等待備件所造成的停機時間已經超過了修復性維修停機時間和預防性維修停機時間[5]。因此,非常有必要對裝備等待備件的時間加以約束。本文以費用作為優化目標,選取裝備的平均等待備件時間作為約束條件。針對壽命分布服從指數分布的備件,運用邊際效應分析方法,計算裝備系統中不同類型備件最優的儲備數量。
1 模型約束條件
在一個供貨周期內,裝備對某種類型備件產生的需求量超過該種備件的庫存數量和已修復的備件數量之和時,超出的備件需求得不到滿足就會導致延期交貨。考慮到只有存在延期交貨,才會出現裝備等待備件的情況,因此平均等待備件的時間和備件的延期交貨量有直接關系。要想得到平均等待備件的時間,必須首先計算備件的延期交貨量。備件的延期交貨量是指當裝備產生備件需求時,沒有被立即滿足的備件的數量,而這些備件需求要等待一段時間后才能被滿足。
備件的延期交貨量EBO的計算公式為

式中:p(x)為部件有x個單元處于維修(再供應)過程的穩態概率;s為備件的庫存數量。
當備件的故障間隔時間服從指數分布且其均值為常數時,則備件的壽命分布服從均值為λt的泊松分布,可由下式表示:
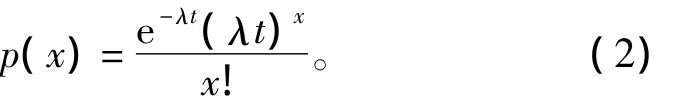
式中:λ為備件需求率;t為備件周轉時間。將式(2)代入式(1),可得:

平均等待備件的時間T就等于備件延期交貨量與備件需求率的比值,可由下式表示[6]:

若裝備系統由n種不同類型的備件構成,則由式(4)可得系統中第i種備件在庫存量為si時平均等待備件時間Ti(si)的計算公式為

式中:si為系統中第i種備件的庫存數量;λi為第i種備件的需求率;EBOi(si)為第i種備件在庫存數量為si時的延期交貨量。
裝備平均等待備件時間T的計算公式為[6]:

式中:SDTi(si)表示編號為i的備件平均等待時間。
2 備件庫存數學模型
選取費用作為優化目標,在保證裝備系統平均等待備件時間低于某一固定值Tm的前提下,使系統級的備件費用最低。數學規劃公式如下:

式中ci為系統中第i種備件的單價。
3 邊際效應分析方法
邊際效應分析是一種漸進的優化算法,用于分配短缺資源來獲取最大的效益。在設定的約束條件下依次進行迭代,直到滿足系統最終的目標值為止。邊際效應分析方法的思想就是,每種備件的數量每次只增加1個,比較增加哪種備件所帶來的優化效益與該備件費用的比值最大,即購買該備件的效費比最高。用邊際效應分析方法求解本問題的步驟如下:
1)確定裝備系統中備件的品種和最初的儲備數量,初始的控制變量si(i=1,2,…,n)的值全部設置為0。
2)確定需要調整的控制變量,尋找最大的邊際效應ΔPi(si)/ci,其計算公式為:

3)分別計算n類備件的ΔPi(si)/ci的值,將最大值對應的備件數量加1。
4)根據所有備件的庫存量si,計算相應的備件延期交貨量,進而計算系統的平均等待備件時間,若小于等于目標值Tm,則迭代完成,否則,進入步驟2繼續迭代。
用邊際效應分析所建立的數學模型流程圖如圖1所示。

圖1 邊際效應分析流程圖Fig.1 Margin utility analysis flow chart
4 實例分析
某裝備系統由 LRU1,LRU2,LRU3,LRU4,LRU5,LRU6和LRU7共7種類型的備件構成,備件的各項參數如表1所示。

表1 備件相關數據Tab.1 Relative data of the spare parts
運用邊際效應分析方法對備件的庫存數量進行優化設計,分析過程如表2所示。在進行了28輪迭代 之 后, LRU1, LRU2, LRU3, LRU4, LRU5,LRU6和LRU7的庫存數量分別為4,4,3,6,3,5,3,計算得到的系統平均等待備件時間為0.902天,小于設定值1天。
通過邊際效應分析方法,由備件的需求率、周轉時間和單價等已知信息,在裝備最小平均等待備件時間的約束下,確定了不同種類的備件各自的庫存量。

表2 邊際效應分析過程數據表Tab.2 Margin utility analysis of process data sheet
5 結語
本文分析了裝備平均等待備件時間與備件的庫存量和備件需求率之間的函數關系,構建了以裝備平均等待備件時間為約束的庫存優化模型,并運用邊際效應分析方法對備件的庫存量進行優化設計,具有重要指導意義。本文沒有考慮裝備因等待備件而導致的停機所造成的損失,在今后的工作中會做進一步研究。
[1]程海龍,康銳,肖波平,等.備件滿足率約束下的備件模型[J].系統工程與電子技術,2007,29(8):1314 -1316.
CHENG Hai-long,KANG Rui,XIAO Bo-ping,et al.Spare model under the constraint of spare sufficiency[J].Systems Engineering and Electronics,2007,29(8):1314 -1316.
[2]王乃超,康銳.基于備件保障概率的多級庫存優化模型[J].航空學報,2009,30(6):1043 -1047.
WANG Nai-chao,KANG Rui.Optimization of multi-echelon repairable item inventory systems with fill rate as objietive[J].Acta Aeronautica Astronautica Sinca,2009,30(6):1043-1047.
[3]程海龍,康銳,龍軍,等.基于邊際效應的備件保障概率庫存優化模型[J].先進制造與管理,2008,27(11):37 -39.
CHENG Hai-long, KANG Rui, LONG Jun, etal.Optimization model on support probability of spare part inventory based on margin utility[J].Advanced Manufacture and Management,2008,27(11):37 -39.
[4]毛德軍,李慶民,張志華.以裝備可用度為中心的保障方案優化方法[J].兵工學報,2011,32(5):636 -640.
MAO De-jun,LI Qing-min,ZHANG Zhi-hua.An optimizing method for availability-centric equipment support plan[J].Acta Armamentarii,2011,32(5):636 -640.
[5]楊秉喜,李金國,張義芳,等.GJB4355,備件供應規劃要求實施指南[S].FL0113,2005.
[6]王乃超,康銳.多約束條件下備件庫存優化模型及分解算法[J].兵工學報,2009,30(2):247 -251.
WANG Nai-chao,KANG Rui.An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J].Acta Armamentarii,2009,30(2):247-251.
[7]王佩高,金家善.隨艦備件動態管理及備件數量計算模型[J].海軍工程大學學報,2005,17(3):103 -106.
WANG Pei-gao,JIN Jia-shan.A calculation model and dynamic management for quantity of spare part on warship[J].Journal of Naval University of Engineering,2005,17(3):103-106.
[8]KENNEDY W J,PATTERSON J W,FREDENDALL L D.An overview of recent literature on spare parts inventories[J].Int J Production Economics,2002,76(2):201 -215.
[9]康銳,李瑞瑩,王乃超,等.可靠性與維修性工程概論[M].北京:清華大學出版社,2010.
[10]王乃超,康銳,程海龍.基于馬爾科夫過程的備件庫存動態特性分析[J].兵工學報,2009,30(7):984 -988.
WANG Nai-chao,KANG Rui,CHENG Hai-long.Study on the dynamic characteristics of spare inventory based on markov process[J].Acta Armamentarii,2009,30(7):984-988.
An optimization model for inventory sapares under the minimum average time for waiting spares
WANG Yu-wen,JIN Jia-shan,CHEN Yan-qiao,WEI Shu-huan
(Power Engineering College,Naval University of Engineering,Wuhan 430033,China)
It expounds the mathematical relationship between the minimum average time for waiting spares and the expected number of backorders in this article.Then,the inventory optimization model is created under the minimum average time for waiting spares of the equipment.Then,optimization approach of spares inventory is described with margin analysis.Finally,predict the number of spares inventory through particular case applying,validate the credibility of the optimization model.
minimum average time for waiting spares;expected number of backorders;margin utility;optimization
TP391.9
A
1672-7649(2013)12-0132-03
10.3404/j.issn.1672-7649.2013.12.027
2013-03-28;
2013-05-08
王玉文(1991-),男,碩士研究生,研究方向為艦船綜合保障工程。

