一種基于慣性匹配的船體姿態基準傳遞方法

袁二凱，楊功流，于 沛，唐 改

(1．北京航空航天大學 儀器科學與光電工程學院，北京100191;2．中國人民解放軍93716 部隊，天津301700)

0 引 言

現代艦船都配備有雷達、導彈發射架、飛機等攻防設備，為保證它們的正常運行，需要艦船為其提供一定精度的姿態、位置等運動參數。艦船上的中心航姿系統是高精度慣導系統或平臺羅經，它可以測量并提供這些參數［1］。但是由于船體變形角的存在，設備安裝點和中心航姿系統之間存在角偏差，直接影響到設備的使用精度。消除船體變形的影響，獲取船體局部高精度姿態信息成為近年來國內外研究的一個熱點問題。目前部分艦船采用光學方法測量主慣導與設備之間的船體變形，在中心主慣導高精度姿態基準上補償變形量以獲取戰位點處的高精度姿態信息，但光學測量系統成本高昂，結構復雜，應用并不廣泛。在各用戶設備處安裝高精度航姿系統成本很高，而且俄羅斯的早期實踐證明這一方法并不完善［2－4］。

本文提出一種基于慣性姿態匹配法實時估計船體變形以實現姿態基準傳遞的方法。在對光學設備測得的船體變形角數據進行頻域分析的基礎上，對船體變形角高精度建模。通過在用戶設備旁邊安裝低精度的捷聯慣導系統，利用中心主慣導與捷聯慣導2 個慣性測量單元(IMU)輸出的姿態信息作為觀測量，建立卡爾曼濾波方程，實現船體變形角的實時最優估計，在主慣導輸出姿態信息的基礎上補償變形量，將高精度姿態基準傳遞給用戶設備。

1 姿態匹配算法

1.1 坐標定義

高精度姿態基準傳遞方法中各系統的安裝位置及坐標定義如圖1所示。IMU1 為船體的中心主慣導，是高精度慣導系統或平臺羅經，全船的姿態信息均以IMU1 的姿態信息為基準，oy 軸沿著船體的縱軸，oz 軸與甲板面相垂直并指向上方，ox 軸與oy、oz 軸構成右手直角坐標系，即為右前上坐標系。IMU2 安裝在用戶設備附近，與IMU1 近似對準，為較低精度捷聯慣導，坐標系為ox′y′z′。姿態基準傳遞方案利用IMU1 和IMU2 的姿態輸出，估計二者之間的實時船體變形角，將IMU1 的高精度姿態信息傳遞到IMU2 所在戰位點。定義ox 方向的船體變形為縱撓角，oy 方向的船體變形為橫撓角，oz 方向的船體變形為首撓角。

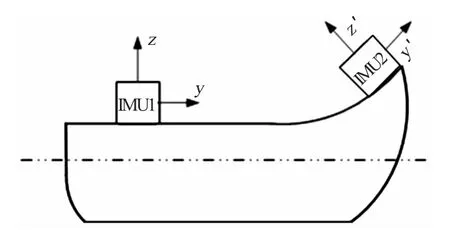
圖1 系統的安裝位置及坐標定義Fig.1 The position of the system and the coordinate definition

對算法中各坐標系定義如下:

定義IMU1 確立的載體坐標系為b1，IMU2 確立的載體坐標系為b2。IMU2 為低精度慣導，由于陀螺漂移等因素的影響，t 時刻IMU2 的計算坐標系會慢慢偏離b2，定義t 時刻IMU2 的計算坐標系b′2。

1.2 姿態匹配算法原理

根據坐標系的定義和坐標變換原理可得:

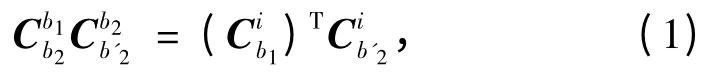
式(1)中左右兩邊狀態轉移矩陣對應的歐拉角相等。記t 時刻2 個IMU 之間的船體變形角為φ對應的姿態歐拉角為θε，則對應的歐拉角可近似為φ+θε。

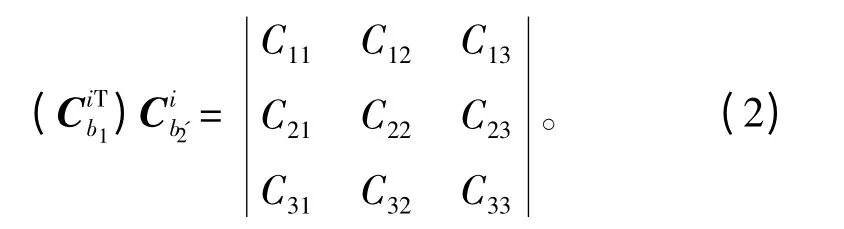
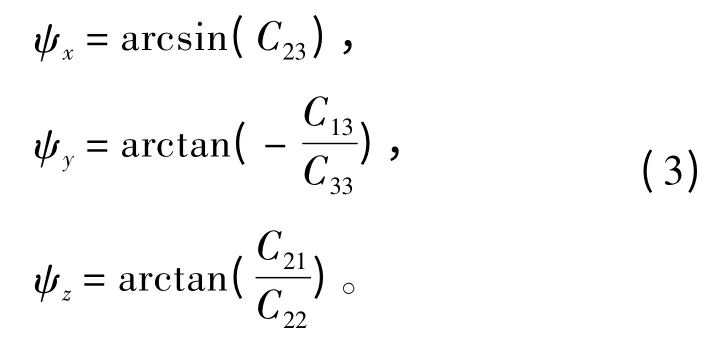
記

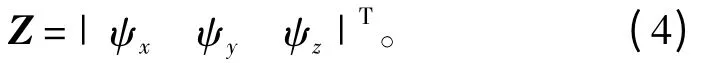
可得

由式(5)可見，2 個IMU 輸出姿態信息，實時變形角與IMU2 姿態誤差角之間存在線性關系，可以此為基礎設計卡爾曼濾波器實現對船體變形角的實時最優估計，從而實現高精度姿態基準的傳遞。

2 船體變形角的高精度建模

研究表明［1］，船體變形的頻率集中在0.3 Hz 以內，由變化較快的動態變形θ 和變化緩慢的靜態變形Φ 兩部分組成。記t 時刻2 個IMU 之間的船體變形角為φ，可得:

為了實現對船體變形角的準確建模，本文選取一段光學設備采集的船體變形實測數據(理論精度達到1″，可近似視為船體的實際變形)進行了頻域分析。

縱撓角的頻譜如圖2所示。圖中頻率低于0.3 Hz 的2 個峰值體現的是船體變形角的頻率特性，高于0.4 Hz 的峰值反映的是由于設備震動產生的噪聲，可以在不影響變形角成分的情況下將其與高頻白噪聲一起濾除。而且從頻率上看，靜態變形和動態變形分布界限明顯:靜態變形頻率集中在0.05 Hz 以內，動態變形集中在0.1 ～0.3 Hz，因此在頻域內將2 種變形分離并建模可行。濾除高頻噪聲和分離2 類變形都可以通過小波分析法實現［7］。

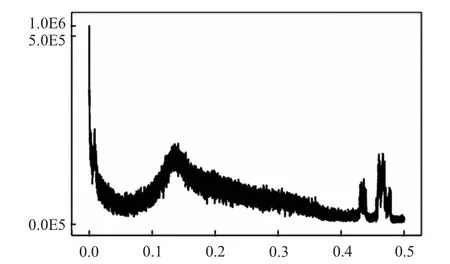
圖2 縱撓角的頻譜圖Fig.2 The spectrum curve of the pitching deformation

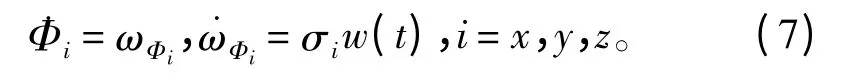
其中，σ 為靜態變形角速率ωΦi的標準差，作為白噪聲的驅動系數，可以在分離靜態變形角后求得。

動態變形θ 可視為二階Markov 過程，其對應的變形濾波器方程可表示為:

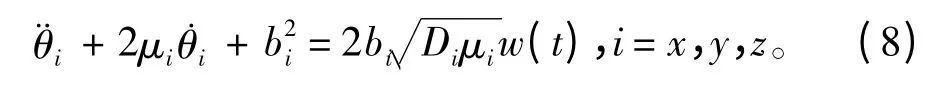
其中，μ 為動態變形不規則系數 (相關時間的倒數);λ 為動態變形的支配頻率;D 為動態變形的方差;b2=μ2+λ2;w(t)為均值為0、方差為1的高斯白噪聲。動態變形的支配頻率λ 即為圖2中0.1 ～0.3 Hz 范圍內峰值對應的頻率。相關時間和方差可以在分離動態變形后通過數學方法解算得到。

通過在頻域內分離靜態變形和動態變形，式(7)和式(8)可以實現對船體變形角的精確建模，并作為狀態量在卡爾曼濾波器中實現最優估計。

3 卡爾曼濾波器模型的建立

3.1 狀態方程的建立

IMU2 的姿態誤差角可表示為:

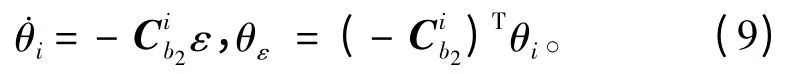
卡爾曼濾波器狀態向量取如下18 維形式:

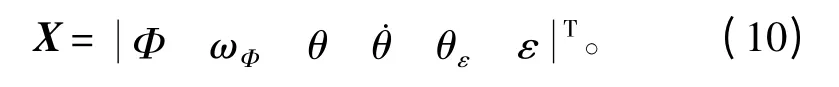
其中:Φ 為靜態變形角;ωΦ為靜態變形角速度;θ為動態變形角;˙θ 為動態變形角速度;θε為IMU2 陀螺漂移造成的姿態失準角;ε 為IMU2 的陀螺漂移。

系統狀態方程的矩陣形式如下:

其中F 為18 ×18 維的稀疏矩陣，由式(8) ～式(10)可得:

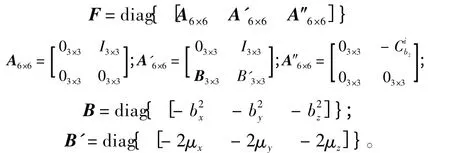
G 為系統噪聲系數矩陣，是18 ×18 維的對角陣，其中非零元素為:

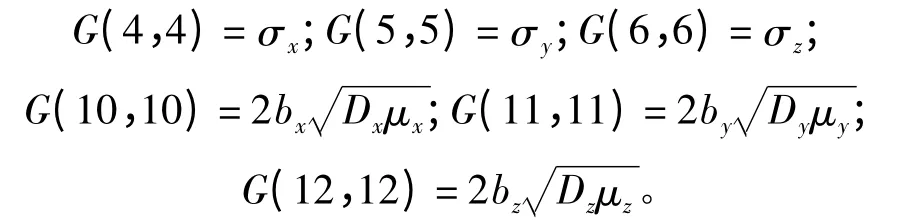
3.2 量測方程的建立

卡爾曼濾波量測方程的矩陣形式為:

Z 的定義如式(4)，由式(6)、式(7)和式(10)得:

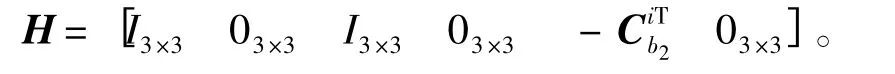
4 仿真驗證與結果分析

4.1 仿真條件

1)船體繞x，y，z 三軸以正弦規律做搖擺運動，繞x，y，z 三軸的搖擺周期分別為8 s，7 s，6 s;搖擺幅度分別為4°，5°，3°;初始水平姿態角為0;航向角為30°;仿真時間50 h。

2)IMU1 作為姿態基準，姿態輸出不含陀螺漂移等誤差信息;IMU2 的姿態輸出是在船體姿態角的基礎上，加入陀螺漂移和船體變形角。IMU2 的x，y，z 三軸陀螺漂移分別為0.005°/h，0.005°/h，0.01°/h;船體變形角將實測船體變形角速度加到IMU2 陀螺的角速度輸出中參與姿態解算。

4.2 仿真結果分析

利用小波分析法濾除高頻噪聲分離靜態和動態變形結果如圖3所示。計算可得動態變形模型參數為:μ=［0.1，0.0625，0.0743］，1/s，λ=［0.13，0.1，0.13］，Hz，D=［9.6 ×10－7，2.25 ×10－5，2.2 ×10－7］，deg;靜態變形模型參數為:σ=［3.7×10－6，2.7 ×10－6，7.3 ×10－7］，deg。

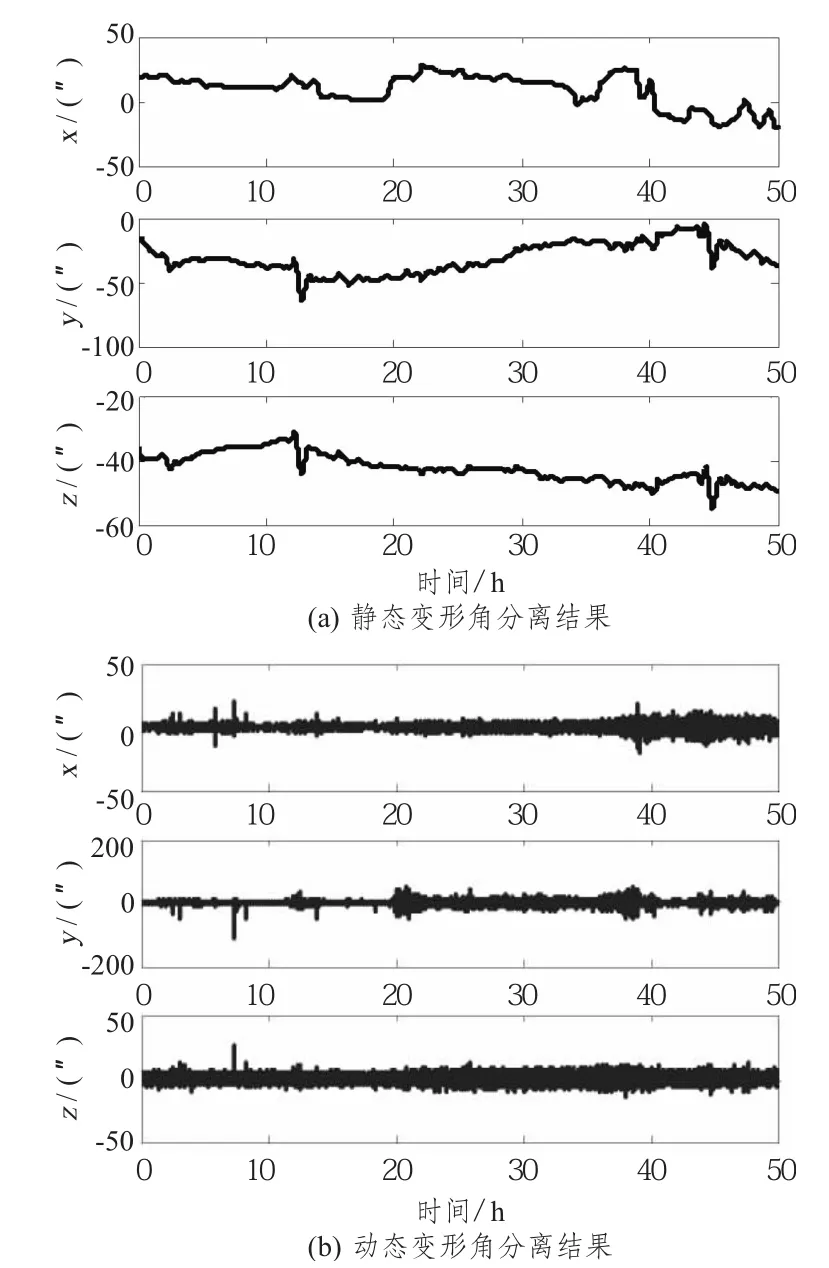
圖3 小波分析法分離靜態和動態變形結果Fig.3 Separation result of static and dynamic deformation

卡爾曼濾波估計結果如圖4所示，算法實現了對船體靜態變形和動態變形的分離估計，IMU2 的x，y，z 三個軸向陀螺漂移分別收斂于0.005°/h，0.005°/h，0.01°/h，與仿真設定值一致。總體變形角的估計結果與理論值對比曲線和估計誤差曲線如圖5所示，船體變形角的估計結果與理論值一致，x，y，z 三個軸向的變形角估計誤差均方差分別為2.3512″，4.565″，3.1242″。姿態匹配算法有效抑制了捷聯慣導陀螺漂移的影響，實現了對船體變形角的高精度實時估計。捷聯慣導所在局部位置的理想姿態為船體中心姿態和局部變形量之和，實現了船體變形角的高精度估計，在中心主慣導高精度測量結果的基礎上補償變形量就能得到設備所在位置的姿態信息，所以局部位置姿態信息的精度取決于中心主慣導的姿態測量精度和船體變形角的估計精度。

捷聯慣導的姿態測量誤差和姿態基準傳遞法得到的姿態誤差對比如圖6所示。捷聯慣導由于陀螺漂移的影響，姿態測量誤差發散較快，姿態匹配算法可以實現船體變形角的實時高精度估計，當中心主慣導的姿態測量結果為理想值時，由于變形角估計均方誤差在5″以內，所以基準傳遞精度可以達到5″以內。

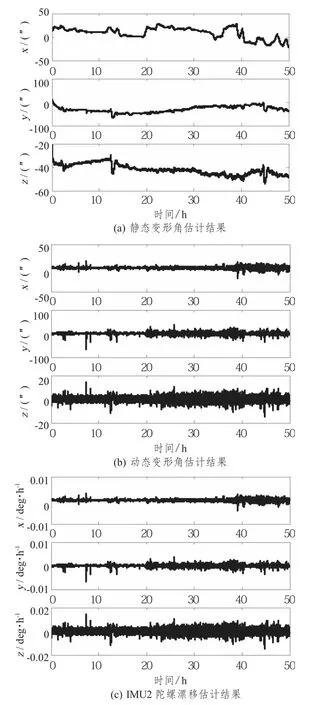
圖4 卡爾曼濾波估計結果Fig.4 Estimation result of the Kalman filter

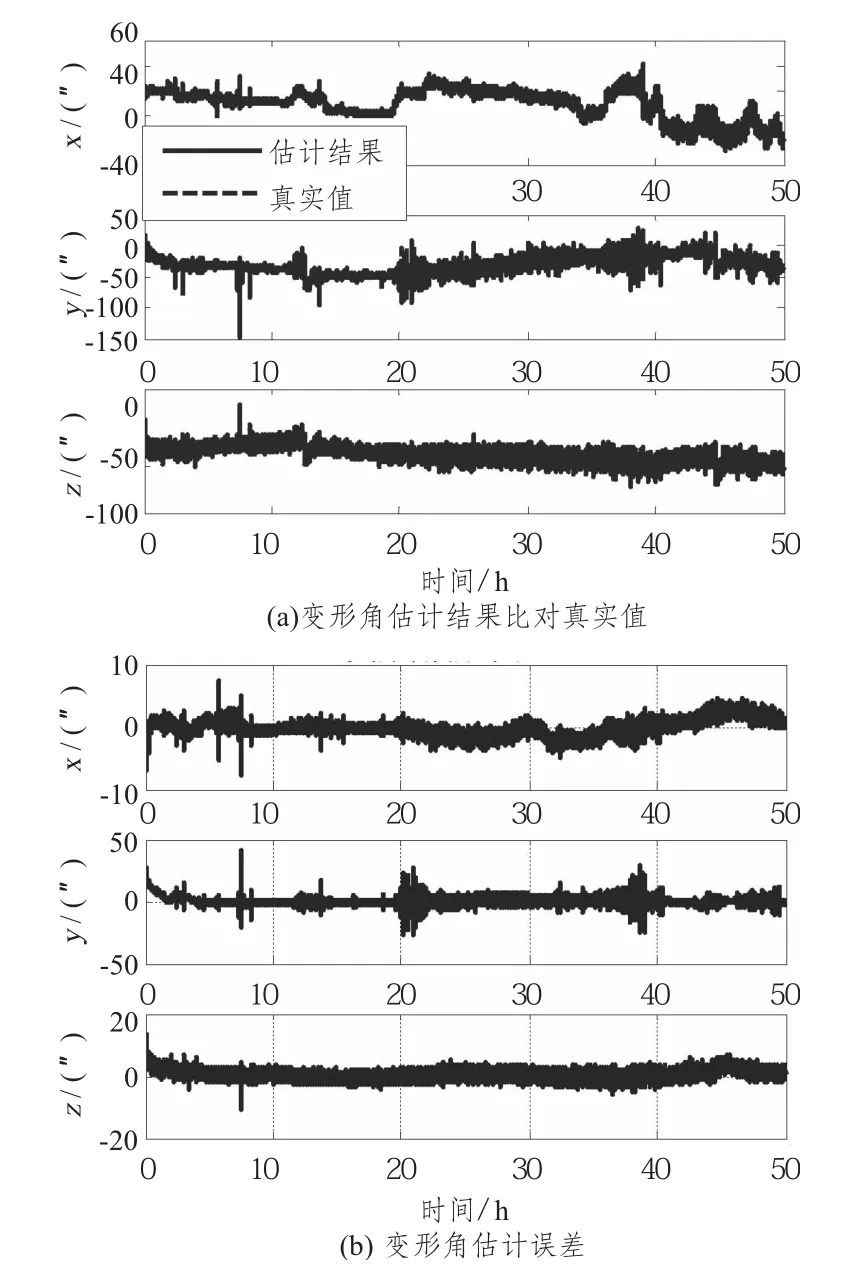
圖5 變形估計結果與理論值對比曲線及誤差曲線Fig.5 Comparison of simulation result and the initial measurement data and the estimation error curve

圖6 姿態測量誤差和姿態傳遞誤差曲線Fig.6 Curves of attitude measurement error and the attitude reference transfer error

5 結 語

本文提出一種基于慣性姿態匹配法實時估計船體變形以實現姿態基準傳遞的方法。姿態匹配法利用中心主慣導和用戶設備處捷聯慣導的姿態輸出構建卡爾曼濾波方程，在對船體變形高精度建模的基礎上，可以實現船體變形角的實時高精度估計，將主慣導高精度的姿態基準傳遞給用戶設備。仿真驗證表明，算法能夠有效抑制低精度捷聯慣導陀螺漂移因素對船體變形估計結果的影響，中心主慣導的姿態測量結果為理想值時，姿態基準傳遞精度在5″以內，說明船體變形角建模方法和姿態匹配算法的可行性，為船體局部高精度姿態信息獲取提供了理論參考。

［1］MOCHALOV A V．A system for measuring deformation of large-sized objects［C］．RTO/ NATO，France，1999，15:1－15．

［2］MOCHALOV A V，KAZANTSEV．Use of the ring laser units for measurement of the moving object deformation［C］．Proceedings of SPIE，2002(4680):85－92．

［3］朱昀炤，汪順亭，繆玲娟，等．船體變形測量技術綜述［J］．船舶工程，2007，29(6):58－61．

ZHU Yun-zhao，WANG Shun-ting，MIAO Ling-juan，et al．Review of measuring technique for ship deformation［J］．Ship Engineering，2007，29(6):58－61．

［4］TITTERTON D H，WESTON J L．Strapdown inertial navigation technology(Second edition)［M］．The Institution of Electrical Engineers，2004．

［5］鄭佳興，秦石喬，王省書．基于姿態匹配的船體形變測量方法［J］．中國慣性技術學報，2010，18(2):175－180．

ZHENG Jia-xing，QIN Shi-qiao，WANG Xing-shu．Ship hull angular deformation measurement taking slow-varying quasi-static component into account［J］．Journal of Chinese Inertial Technology，2010，18(2):175－180．

［6］SCHNEIDER A M，Kalman filter formulations for transfer alignment of strapdown inertial units［J］．Journal of the Institute of Navigation，1983，30(1):72－89．

［7］WEN M．Spectrum denoise by wavelet analyze and its realize in Matlab［J］．Modern Electronics Technique，2003，26(24):47－49．