水下生產系統臍帶纜溫度場與載流量分析的有限元方法

郭 宏， 高 歡

（1.中海油研究總院，北京100027；2.上海電纜研究所，上海200093）

水下生產系統臍帶纜溫度場與載流量分析的有限元方法

郭 宏1， 高 歡2

（1.中海油研究總院，北京100027；2.上海電纜研究所，上海200093）

為解決傳統熱路法計算載流量的局限性，采用有限元軟件ANSYS對復雜結構的臍帶纜模型進行分析，得出其整體結構溫度場分布情況，對比不同纜芯結構中溫度場分布的差別，得出了載流量的優化確定方法。

臍帶纜；載流量；有限元

0 引 言

經濟的快速發展必然導致人類對能源需求的加大，尤其是不可再生資源石油，作為國家經濟的血液，石油的儲存量越來越少，為緩解這種現狀，加快海洋油氣資源開發已成為國家戰略需求。水下生產系統臍帶纜（以下簡稱臍帶纜）作為水下生產作業設備的生命線，在我國長期以來依賴進口，對這一方面的關鍵技術研究尚屬空白，因而在一定程度上制約了我國深海油氣田的開發［1］。

從國內外發展現狀來看，發達國家對水下生產系統臍帶纜的研究已較為成熟［2］，國外很多學者采用解析和數值方法對臍帶纜整體和截面進行了分析，但這些分析大多是關于力學性能方面的研究［3］，關于電場、溫度場的分析較少。

研究臍帶纜的載流量、各部分溫度分布是確保臍帶纜安全可靠運行的基礎［4］。傳統熱路法由于其計算存在局限性，不適于計算結構復雜的臍帶纜中溫度場分布，因此本文采用有限元法確定臍帶纜載流量與各部分溫度。

1 水下生產系統臍帶纜簡介

水下生產系統臍帶纜的主要作用是連接上部模塊與水下生產設施，主要由電纜（動力纜或信號纜）、光纜（單模或多模）、液壓或化學藥劑管（鋼管或軟管）、聚合物護套、鎧裝鋼絲以及填充物等組成。臍帶纜各單元排布上講求對稱、緊湊和圓整，本文將對兩種典型臍帶纜纜芯結構進行載流量分析（見圖1）。

2 傳統熱路法計算電纜載流量

根據電纜絕緣材料的種類、運行和使用經驗，各種型式電纜的長期和短時允許最高工作溫度都有規定。一般說來，如果電纜長期和短時工作溫度不超過規定值，電纜應能在至少15年內安全運行；反之，如果電纜工作溫度過高，絕緣材料老化就會加速，電纜壽命就會縮短，甚至立刻遭到破壞。因此，在設計或選用電纜時，除了充分考慮電氣、機械性能外，還應仔細分析其熱性能，使電纜在保證傳輸容量的條件下，各部分損耗發熱不致超過電纜允許最高溫度。

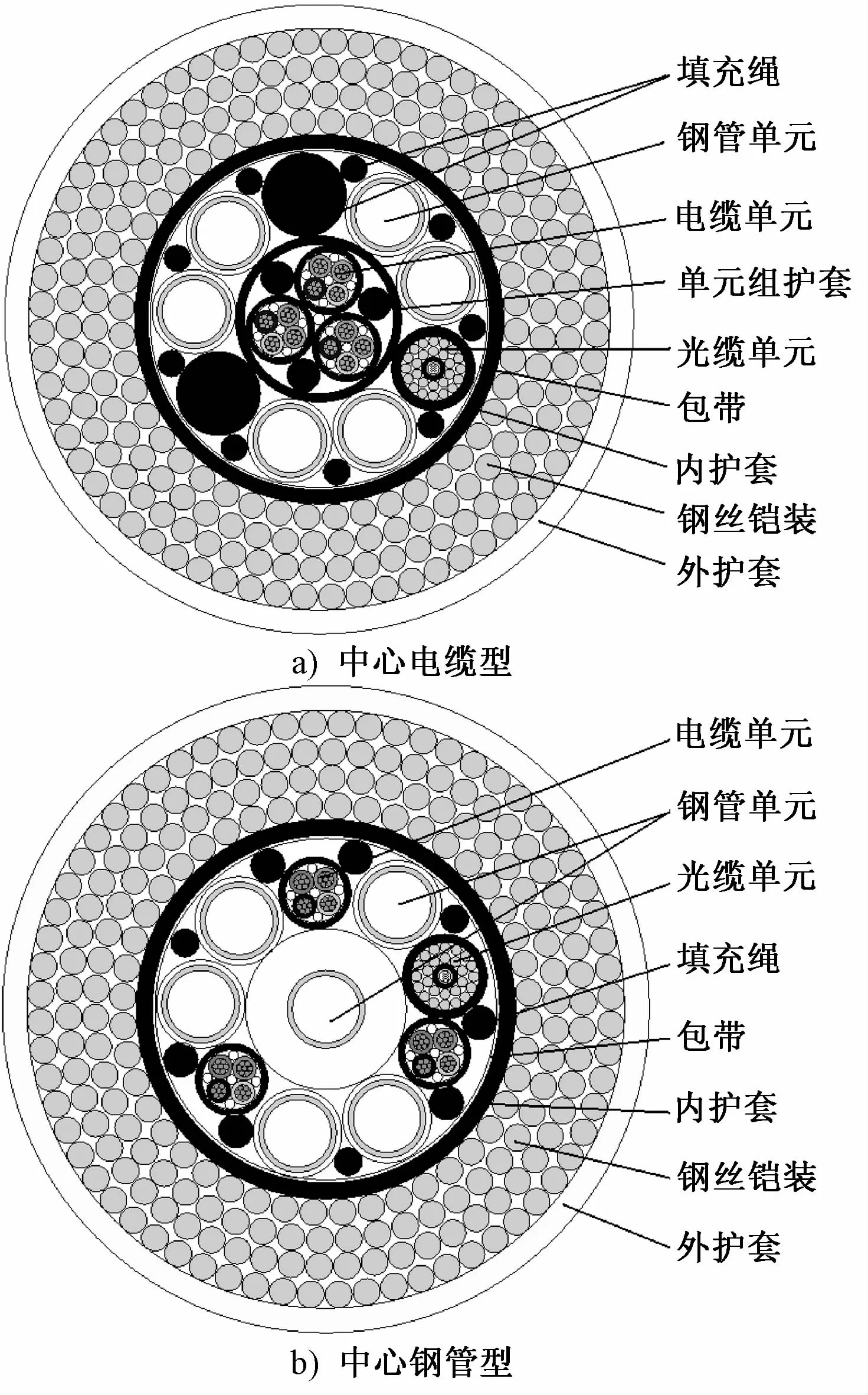
圖1 典型的臍帶纜結構示意圖

通常，根據熱路法計算使線芯導體達到最大允許溫度時的連續電流，原理如圖2所示。

圖2 載流量熱路計算原理

對于特定結構電纜，參照各類標準，可以根據電纜結構及敷設條件給出等值熱路，求出線芯電阻及電纜和周圍媒質的熱阻，最后列出電纜熱平衡方程，即可得電纜恒定負載連續額定載流量。但由于海底臍帶纜內部結構復雜，且敷設環境比較特殊，所以傳統的計算方法無法滿足要求。

3 穩態載流量計算的有限元法

3.1 有限元方法

穩態溫度場的研究基于以下假設：

（1）多芯扭絞導線等效為截面面積相等的單芯圓導線，電纜材料的傳熱參數為常數；

（2）電纜負荷電流和環境溫度不變，溫度分布不隨時間變化，不考慮電纜分布電容對溫度分布的影響；

（3）內熱源發熱均勻，熱流由里向外流。

考慮到電纜長度遠大于其截面積，電纜穩態溫度場屬于含有內熱源的二維平面導熱分析。對于臍帶纜，由于其特殊的組合式結構，使得其散熱與溫度分布計算更為復雜，對于具有內熱源的固體，熱傳導的偏微分方程為：

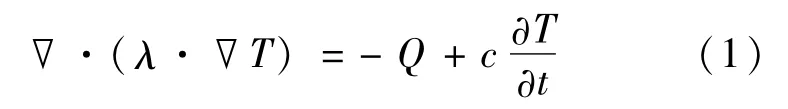
式中，T為溫度場內各點溫度；λ、c、Q分別為微元的導熱系數、比熱、導熱量。

對于臍帶纜情況符合第三類邊界條件，即已知對流換熱系數與流體溫度，其平衡方程組為：

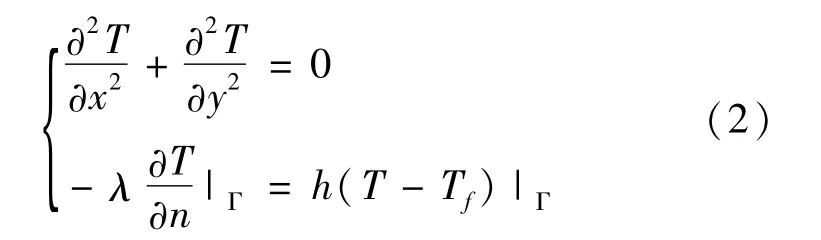
式中，λ為導熱系數［W/（m·K）］；h為對流換熱系數［W/（m·K）］。

溫度場分析即對臍帶纜整個區域進行總體合成，得到相應的矩陣，求解后可以得到各點溫度值。實際臍帶纜絕緣結構溫度場分析中上述矩陣的求解是借助大型有限元軟件來實現的［5-6］。ANSYS作為大型通用有限元分析軟件，它在分析溫度場方面有著許多別的軟件不可比擬的優勢，ANSYS程序有著良好的圖形界面，Workbench界面操作起來，其快速的網格劃分功能以及強大的結果后處理功能，都讓分析得心應手。

3.2 計算流程

一般有限元分析步驟如下：首先利用軟件自帶建模平臺或借助第三方CAD軟件建立分析所對應的二維或三維模型；而后對模型中涉及到的各部分材料相關特性參數進行分別定義；選擇適當的三角或其它單元類型與網格精度劃分計算網格；在對應邊界加載各種正確的載荷條件；最后運行求解器，進行有限元計算，得到各單元溫度分布情況。本文分析臍帶纜溫度場的流程如圖3所示。

3.3 熱負荷計算與加載

根據上面分析的熱平衡控制方程和邊界條件可以看出，若要計算溫度場的分布，除了邊界條件為已知值外，還需獲得場域內熱源的單位發熱率。對于電纜單元，其熱源主要有導體交流損耗、絕緣層介質損耗和金屬層渦流損耗。

單位長度的電纜內導體的發熱功率PC為：

式中，IC為導體負荷電流；RC為導體交流電阻。考慮到導體集膚效應和鄰近效應的影響，導體交流電阻RC為：

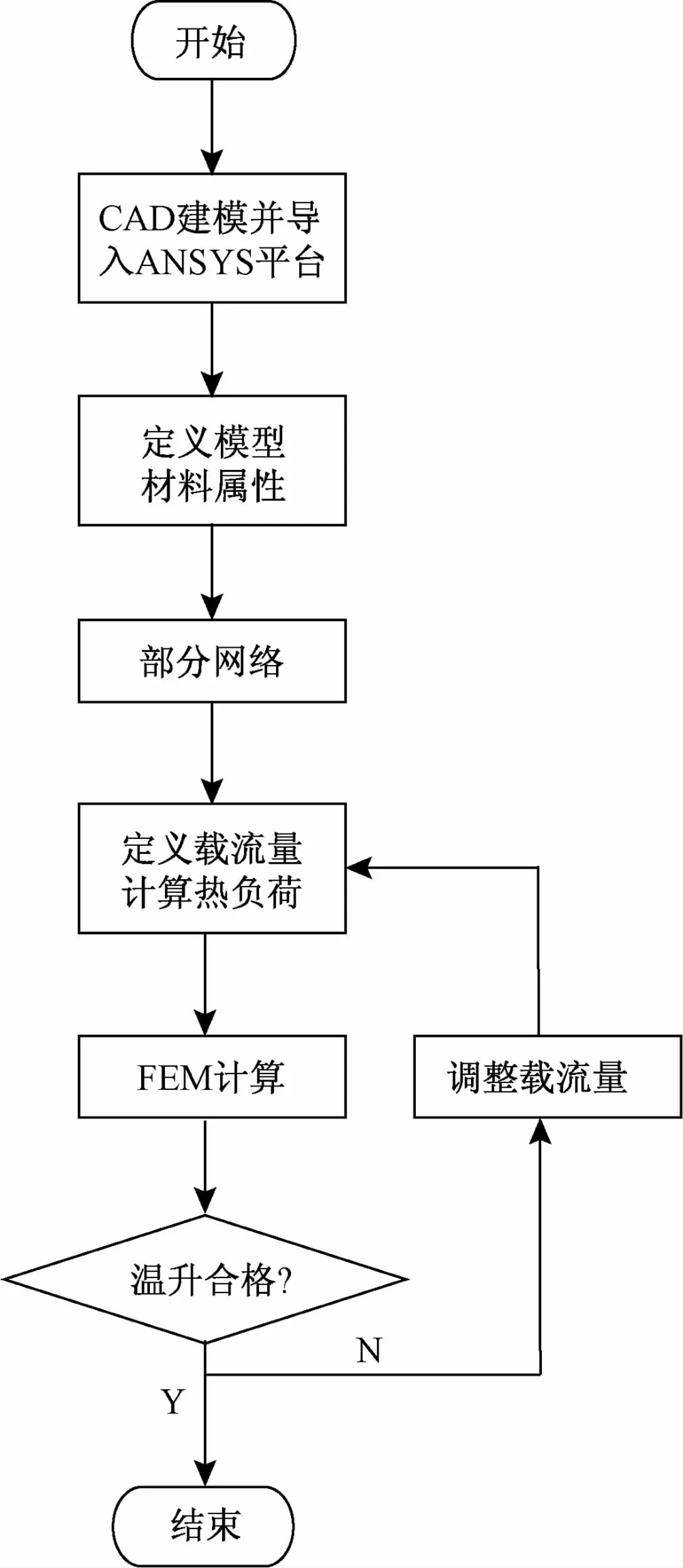
圖3 ANSYS溫度場分析流程

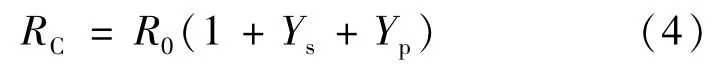
式中，R0為導體在20℃時的直流電阻；Ys為導體集膚效應系數；Yp為導體鄰近效應系數。

除導體損耗外，結構的發熱還與絕緣材料有關，根據電介質物理理論，介質損耗與外施電壓及材料特性有關，每相單位長度的介質損耗PD為：

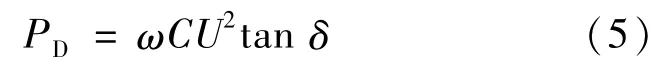
式中，ω=2πf；C為單位長度電纜電容（F/m）；U為相電壓（V）；tanδ為材料介質損耗因數。

由于計算的臍帶纜電壓等級并不高，而且電纜單元絕緣一般采用聚乙烯等非極性材料，tan值極小，因而這部分損耗也較小，一般可忽略不計。

在大多數情況下，電纜金屬護套（包括鎧裝）要求牢固接地，因為這樣的聯接方法簡單，可以免除護套中感應電勢造成對電纜安全運行的危害，同時系統往往需要金屬護套作為接地電流通路，因此會產生損耗。電纜金屬護套損耗的計算中，多芯電纜的線芯中電流之和為零，且線芯的幾何中心重合時，多芯電纜護套中感應電動勢和損耗才等于零，而事實上，線芯的幾何中心并不重合，他們之間的距離和線芯直徑是同一數量級的數值。因此，多芯電纜護套中的損耗并不等于零，只是比單芯電纜護套中損耗小得多，為便于分析，暫不考慮影響。

4 結果與分析

實際計算采用四層鎧裝臍帶纜結構，實際分析計算的導體線芯面積6.0 mm2，對比中心電纜和中心鋼管兩種結構，詳細的溫度場模型單元剖分如圖4所示。對兩種截面的臍帶纜進行熱分析，結果如圖5所示。圖5a為中心電纜單元的端面結構，在臍帶纜管單元內液體最大工作溫度為70℃，工作電流31A時，臍帶纜最熱點溫度為89.885℃，接近交聯聚乙烯的允許溫度90℃。

圖4 臍帶纜計算單元剖分

圖5b為中心鋼管單元的臍帶纜端面結構，在臍帶纜管單元內液體最大工作溫度同樣為70℃，工作電流58A時，臍帶纜最熱點溫度為88.974℃，接近交聯聚乙烯的允許溫度90℃。可見，中心電纜單元的散熱情況極差，其理論載流量僅為中心管單元的53%，實際設計臍帶纜端面結構時應盡量避免采用電纜單元位于臍帶纜中心部分的絕緣結構。

可見，采用有限元分析的方法分析復雜結構的溫度情況，得出最熱點溫度值，可以最終得到電纜導體的理論載流量值。這種分析方法比傳統的熱阻熱路計算法更適宜復雜截面或特殊環境下的電纜載流量計算。

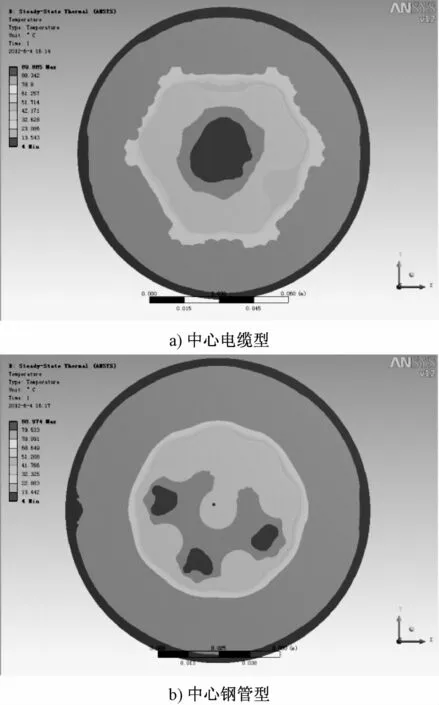
圖5 不同纜芯結構溫度分布

5 優化確定載流量

一般有限元熱分析過程中，在對應邊界加載各種正確的載荷條件，然后運行求解器，進行有限元計算，得到各單元溫度分布情況。在此分析過程中，電流載荷的施加對最終溫升的計算結果至關重要，傳統有限元計算分析往往采用試湊方法，分析計算效率差，因此有必要采用更加優化的計算方法，快速準確地得到項目的額定理論載流量值。

（1）在ANSYS中，將施加載荷時的Heat Flux和求解后所得的最大溫度Temperature分別設置成輸入參數和輸出參數；

（2）選擇Goal Driven Optimization優化子項，啟動GDO分析，在Design of Experiments中，選擇DOE中心組合設計（Central Composite Design）類型；

（3）在Optimization study中選擇輸入參數P2（熱流量值）為尋求最大值“Maximize”，輸出參數P1（最高溫度）為目標值，小于或等于90℃，更新優化可得優化曲線，對應曲線上90℃點的熱流量即為理論載流量所對應的熱流量值，如圖6所示。

（4）根據優化得到的熱流量值，銅導體截面6 mm2，考慮導體電阻損耗時，可按照下式求得載流量In。

式中，P2為熱流量值（W/m2）；S為單位長度導線散熱面積（m2）；R為單位長度導線電阻（Ω/m）；A為導線截面積（mm2）；ρ20為銅導體20℃電阻率，取0.0175Ω·mm2/m；α為銅導體電阻溫度系數，取0.0039/℃。

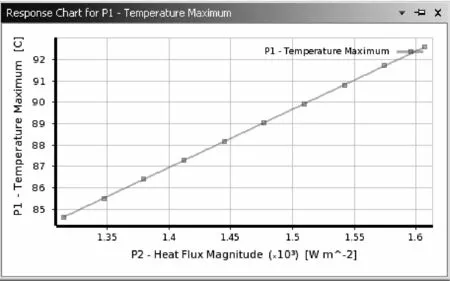
圖6 載流量優化曲線

根據式（6），當電纜絕緣達到交聯聚乙烯的允許溫度90℃時，中心鋼管單元臍帶纜的載流量理論計算結果為In=59.4 A。

6 結束語

臍帶纜是由電纜、光纖、不銹鋼管等多種結構單元組成的復雜組合體，涉及多種工程材料，必須采用有限元數值分析求出臍帶纜復雜截面各部分溫度實際分布情況，計算其最熱點溫度，從而找到最熱點，驗證整體結構在運行中的長期散熱合理性，同時按照有限元溫度場分析，可以得到實際的載流量。

本文采用基于有限元法的ANSYS軟件對不同結構臍帶纜溫度場進行分析，通過對臍帶纜結構溫度場的分析發現，臍帶纜端面各單元、各部件之間的空氣隙比例越少，結構散熱效果好，載流量也越大。對溫度場分布而言，其分布受纜芯結構的影響較大，當電纜單元集中在中心位置時，散熱情況較差，此時載流量僅為中心管單元結構的53%，應當避免在設計臍帶纜時要避免將電纜單元置于中心位置。

［1］ 李長春，連 璉.水下生產系統在海洋石油開發中的應用［J］.海洋工程，1995，13（4）：25-30.

［2］ Witz J A，Tan Z.On the axial-torsional structural behaviour of flexible pipes，umbilicals and marine cables［J］.Marine Struetures，1992，5：205-227.

［3］ 高 歡，郭 宏，孫科沸，等.水下生產系統臍帶纜初步結構設計［J］.電線電纜，2011（6）：12-16.

［4］ 曹惠玲，王增強，李雯靖.坐標組合法對直埋電纜與土壤界面溫度場的數值計算［J］.電工技術學報，2003，18（3）：59-63.

［5］ 溫嘉斌，許明宇.防爆型水冷電機內換熱與溫度場計算［J］.電機與控制學報，2009，13（3）：393-397.

［6］ 張沛紅，單 濤，時亞娟.變壓器端部絕緣結構參數化設計及電場分析［J］.哈爾濱理工大學學報，2012，17（2）：76-79.

The Finite Element M ethod of Tem perature Field and Am pacity Analysis of Umbilical Cable

GUO Hong1，GAO Huan2
（1.CNOOC Research Institute，Beijing 100027，China；2.Shanghai Electrical Cable Research Institute，Shanghai200093，China）

The finite elementmethod was used in this paper solving the limitation of traditional thermal circuitanalyticalmethod.The software of ANSYSwas used to analyze the submarine umbilical cablesmodels with complex structure，and results of the whole temperature field distribution were shown by comparing the difference of temperature field distribution in different cables.Moreover，the optimum calculatingmethod of ampacity is given for design of umbilical cables.

umbilical cable；ampacity；finite elementmethod

TM247.9

A

1672-6901（2013）03-0005-04

2013-03-01

國家863計劃資助項目（2009AA09Z301-1）

郭 宏（1968-），女，高級工程師.

作者地址：北京市東城區東直門外小街6號［100027］.