圖像法處理打點紙帶的研究

何述平

（西北師范大學教育學院物理教育研究所，甘肅 蘭州 730070）

1 引言

打點紙帶的數據處理是研究勻變速直線運動實驗的基本而重要的內容，也是打點計時器在中學物理實驗應用的基本方法.然而，關于處理打點紙帶的圖像法，以前雖有所論述；［1－4］但較零星、籠統，有必要再進行較深入、系統的探究，進而為合理處理打點紙帶奠定層次性、開放性的理論基礎.本文就此進行相應的研究，以期拓展處理打點紙帶測定加速度、初速度的圖像法，提供實驗數據處理的圖像法依據，并為打點計時器的實驗教學設計奠定堅實的物理基礎.

2 圖像法的推證

紙帶隨物體做勻變速直線運動，打點紙帶的計數點為n，計數周期為T，連續計數點間的位移依次為s1，s2，…sn，sn＋1…，如圖1所示.

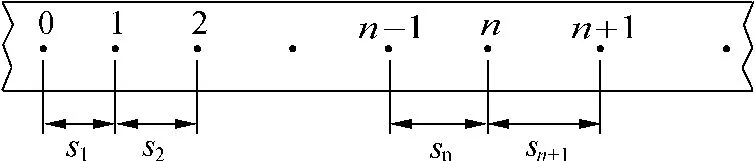
圖1

計數點n－1、n間的位移為

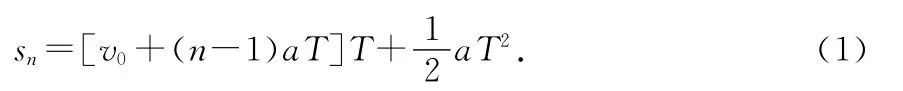
式中n＝1，2，3，…，v0為n＝0時的瞬時速度.

計數點n的瞬時速度為

2.1 基本圖像法

2.1.1 位移圖像法

由式（1）得

式中

為恒量，取決于實驗條件、計數點的選取（物理意義為：n＝0、前T內的位移）.

依據式（3）有以下3種具體位移圖像法.

2.1.1.1 s－t圖像法

式（3）可改寫為［2］

式（5）表明：sn與nT呈一次線性關系.于是按圖像法處理數據（nT，sn），就可確定加速度as－t.

2.1.1.2 s－n圖像法

式（3）可改寫為［2，3］

式（6）表明：sn與n呈一次線性關系.于是按圖像法處理數據（n，sn），就可確定加速度as－n.

2.1.1.3 s－t2圖像法

式（3）可改寫為

式（7）表明，sn與nT2呈一次線性關系.于是按圖像法處理數據（nT2，sn），就可確定加速度as－t2.

另外，分別由位移圖像法確定的as－t、as－n、as－t2 和s0代入式（4），就可確定初速度v0.

2.1.2 速度圖像法

依據對速度圖像法的理解層次不同，可進行分類：從物理實驗數據處理的形式上理解，就是基本速度圖像法；從物理實驗數據處理的實質上理解，則是變形速度圖像法.

（1）基本速度圖像法.

紙帶做勻變速直線運動，則有

式中n＝1，2，3，…依據式（8）有以下兩種具體基本速度圖像法.

（a）v－t圖像法.

式（8）可改寫為［1－4］

式（9）表明：vn與nT 呈一次線性關系.圖像法處理數據（nT，vn），就可確定加速度av－t、初速度v0.

（b）v－n圖像法.

式（8）可改寫為

式（10）表明：vn與n呈一次線性關系.圖像法處理數據（n，vn），就可確定加速度av－n、初速度v0.

（2）變形速度圖像法.

由式（2）知，速度vn并非實驗的直接測定量，有必要將其表示成實驗的直接測定量——位移sn、時間T的函數.于是，將式（2）代入式（8）得

依據式（11）有以下3種具體變形速度圖像法.

式（11）可改寫為

式（12）表明，sn＋sn＋1與2nT 呈一次線性關系.圖像法處理數據（2nT，sn＋sn＋1），就可確定加速度asv－t、初速度v0.

（b）sv－n圖像法.

式（11）可改寫為

式（13）表明：sn＋sn＋1與2n呈一次線性關系.圖像法處理數據（2n，sn＋sn＋1），就可確定加速度asv－n、初速度v0.

（c）sv－t2圖像法.

式（11）可改寫為

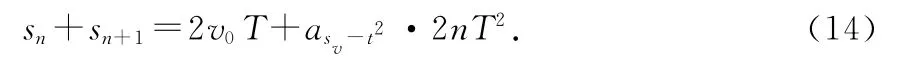
式（14）表明：sn＋sn＋1與2nT2呈一次線性關系.圖像法處理數據（2nT2，sn＋sn＋1），就可確定加速度 asv－t2、初速度v0.

當滿足上述高度調整閥調平條件時，僅通過高度調整閥即可調平；若不能同時滿足，則需分別在前后轉向架軸箱彈簧處加設墊片來減小|ΔB1|和|ΔB2|，從而使調平條件滿足要求。由于|ΔB1|和|ΔB2|分別能反映前、后轉向架的調平情況，為了節約調平時間，降低工藝難度和復雜度，當需要在軸箱彈簧處加設墊片時，工人希望盡量只在一個轉向架的軸箱彈簧上加設。為此，可以先比較|ΔB1|和|ΔB2|的大小，再進一步計算能否通過只減小|ΔB1|和|ΔB2|中較大者來滿足高度調整閥調平條件。

2.2 奇異圖像法

從不同角度或側面考慮同一問題，也許是有益的；這形成了處理打點紙帶的奇異圖像法.

2.2.1 中時速度圖像法

紙帶做勻變速直線運動，則有

式中n＝1，2，3，…，v0′為n＝0 （時的瞬時速度 n想象為比圖1中計數點超前而

2.2.1.1 基本中時速度圖像法

式（15）可分別改寫為

由式（17）、（18）分別按圖像法處理數據（nT，vn′）、（n，vn′），可確定加速度av′－t、av′－n和v′0.

另外，由勻變速直線運動的速度規律，有

由式（19）、圖像法確定的av′－t、av′－n和v0′可確定初速度v0.

2.2.1.2 變形中時速度圖像法

式（16）代入式（15），得

式（19）代入式（20），得式（3）、（4）；進而有式（5）、（6）、（7），即有位移圖像法的結果.可謂殊途同歸.

2.2.2 線性化圖像法

參照圖1，紙帶做勻變速直線運動，則有

式中n＝1，2，3，…，v0為n＝0時的瞬時速度.

將式（21）線性化［5］，得

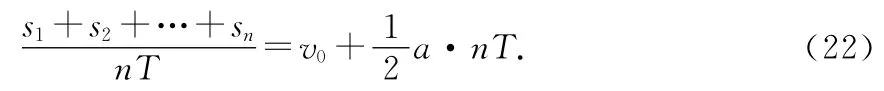
由式（22）則有如下兩種具體線性化圖像法.

式（22）可改寫為

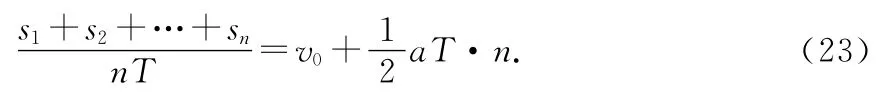
3 圖像法的分類

圖像法具有直觀、簡便的特點，［5，6］因此在物理實驗數據處理中有重要運用；但隨著作圖工具的發展，圖像法也不斷發展；依據目前作圖工具，圖像法可分為人工圖像法和機工圖像法.就物理實驗教學而言，人工圖像法即手工作圖，簡稱為作圖圖像法，因手工作圖不可避免地存在一定的作圖誤差，［5］從而有一定運用（如分析物理量間關系，粗略求物理量值）；機工圖像法即計算機作圖圖像法，是回歸法與計算機的計算、圖像功能相結合的方法，計算機有現成的Excel程序能自動完成數據處理，不僅可獲得線性函數的回歸法圖像，而且可獲得線性函數的回歸法表達式，［6］從而有廣泛運用（如擬合物理量間關系，精確求物理量值，定量確定標準差，預報與反預報），由此形成了可簡稱為回歸圖像法.

幸運的是，上述推證的12種圖像法中的因變量與自變量均呈一次函數關系；因此可直接進行直線回歸或擬合，即可直接運用回歸圖像法處理打點紙帶數據.

4 圖像法的運用及結果

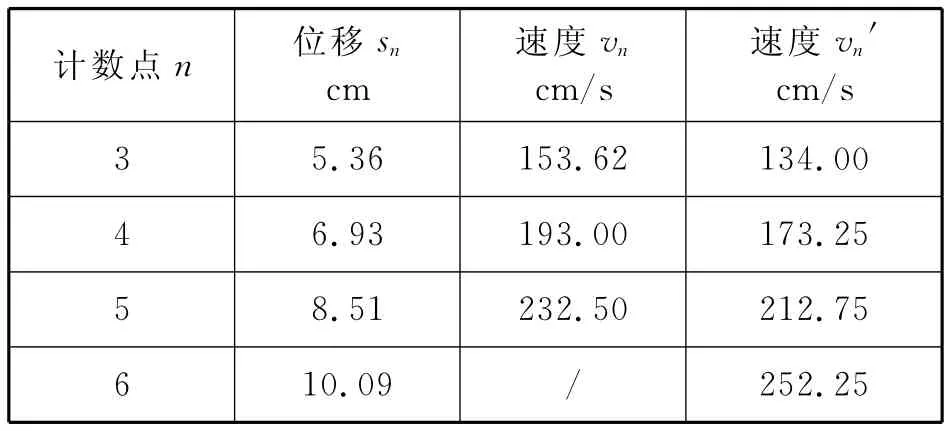
取測定北京地區重力加速度（g北京＝980.12cm／s2）的打點紙帶數據（T＝0.04s）［3］，如表1（vn、vn′分別由式（2）、（16）算得）；則依次運用上述推證的回歸圖像法（Excel程序：選定（xi，yi）→插入→圖表→標準類型→XY散點圖→平滑線散點圖→完成；右擊平滑圖線→添加趨勢線→類型→線性→選項→顯示公式→確定）處理打點紙帶測定加速度、初速度的結果如表1.

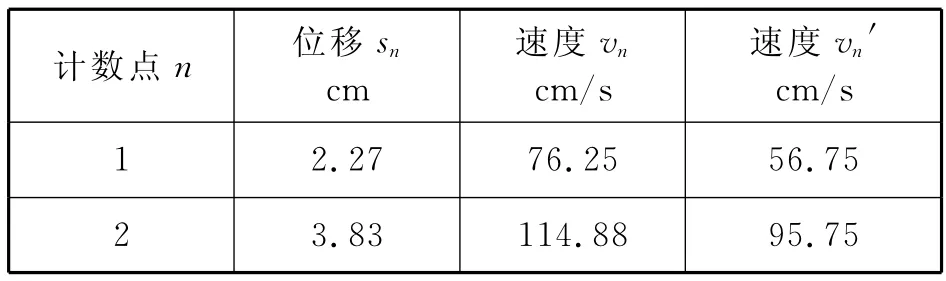
表1

續表

4.1 位移圖像法的結果

（1）由式（5）、表1相應數據得s－t圖像、表達式，如圖2；進而得：gs－t＝976.98cm／s2，v0＝36.89cm／s.

圖2

（2）由式（6）、表1相應數據得s－n圖像、表達式，如圖3；進而得：gs－n＝976.88cm／s2，v0＝36.89cm／s.

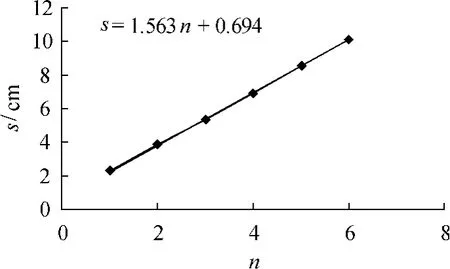
圖3

（3）由式（7）、表1相應數據得s－t2圖像、表達式，如圖4；進而得：gs－t2＝976.96cm／s2，v0＝36.89cm／s.

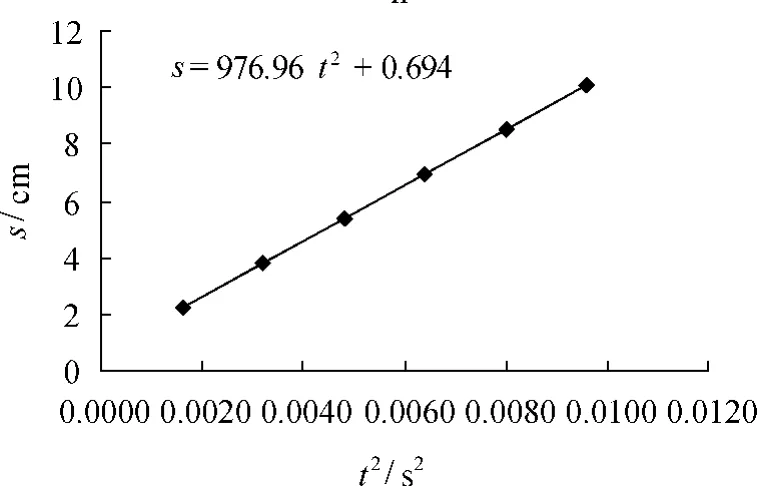
圖4

4.2 速度圖像法的結果

4.2.1 基本速度圖像法的結果

（1）由式（9）、表1相應數據得v－t圖像、表達式，如圖5；進而得：gv－t＝976.55cm／s2，v0＝36.86cm／s.

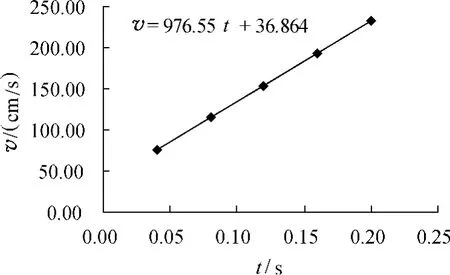
圖5

（2）由式（10）、表1相應數據得v－n圖像、表達式，如圖6；進而得：gv－n＝976.55cm／s2，v0＝36.86cm／s.

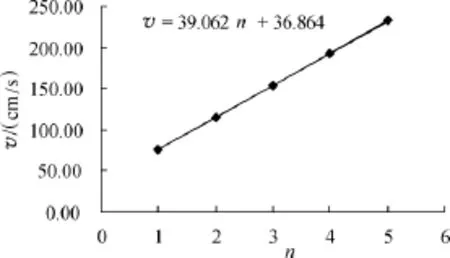
圖6

4.2.2 變形速度圖像法的結果

（1）由式（12）、表1相應數據得sv－t圖像、表達式，如圖7；進而得：gsv－t＝976.58cm／s2，v0＝36.86cm／s.

圖7

（2）由式（13）、表1相應數據得sv－n圖像、表達式，如圖8；進而得：gsv－n＝976.56cm／s2，v0＝36.86cm／s.

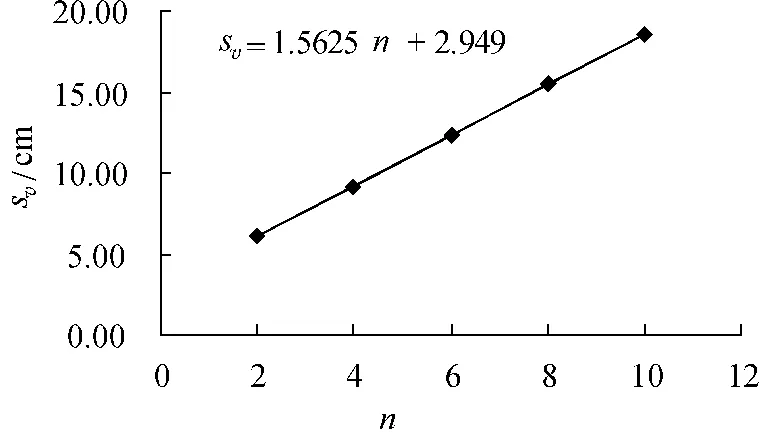
圖8

（3）由式（14）、表1相應數據得sv－t2圖像、表達式，如圖9；進而得：gsv－t2＝976.56cm／s2，v0＝36.86cm／s.

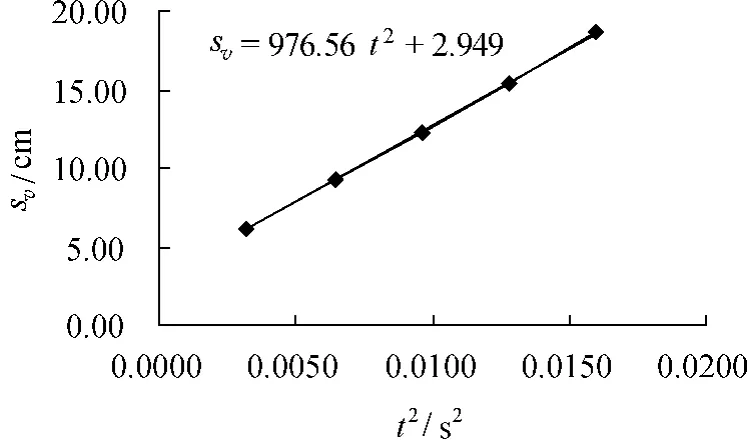
圖9

4.3 中時速度圖像法的結果

（1）由式（17）和表1中相應數據得v′－t圖像、表達式，如 圖 10；進 而 得：gv′－t＝976.96cm／s2，v0＝36.89 cm／s.

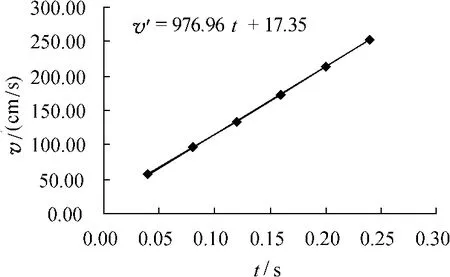
圖10

（2）由式（18）和表1中相應數據得v′－n圖像、表達式，如圖11；進而得gv′－n＝976.98cm／s2，v0＝36.89cm／s.

圖11

4.4 線性化圖像法的結果

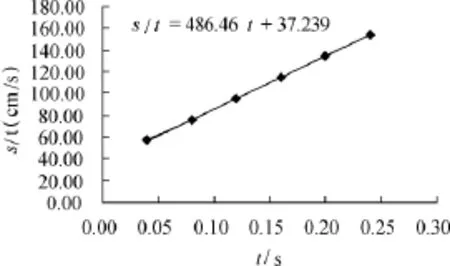
圖12

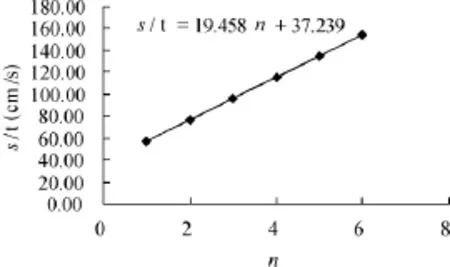
圖13

上述12種圖像法處理打點紙帶數據的結果表明：12種圖像法的結果基本一致（重力加速度的相對誤差依次為0.32%，0.33%，0.32%；0.36%，0.36%；0.36%，0.36%，0.36%；0.32%，0.32%；0.73%，0.74%）；因摩擦、空氣阻力，則實驗測定值g實測應比公認標準值g北京偏小.因此，各圖像法的結果具有合理性；進而說明各圖像法具有合理性、可行性.

5 圖像法的討論

5.1 特點比較

位移圖像法的式（3）、基本速度圖像法的式（8）、變形速度圖像法的式（11）、基本中時速度圖像法的式（15）、變形中時速度圖像法的式（20）、線性化圖像法的式（22）不僅物理意義明確（式（22）表明：時段nT的平均速度即中間時刻的瞬時速度，等于初速度v0加上一半時段的速度增量；則其物理實質是勻變速直線運動的速度變化規律），而且可以互推（如由式（3）、（4）可推得式（11），由式（11）、（4）可推得式（3）；由式（3）、（4）可推得式（8），由式（8）、（4）可推得式（3）（參考圖1）；由式（8）、（2）可推得式（11），由式（11）、（2）可推得式（8）；由式（15）、（16）可推得式（20），由式（20）、（16）可推得式（15）；由式（20）、（19）可推得式（3），由式（3）、（4）可推得式（20）；由式（3）、（4）可推得式（22），由式（22）、（4）可推得式（3）；由式（8）、（19）可推得式（15），由式（15）、（19）可推得式（8）等等）；雖表達形式上不同，但物理實質等效（從不同側面即位移、速度反映勻變速直線運動的特征——加速度恒定）.

比較上述各圖像法可知，圖像法處理打點紙帶測定加速度的簡捷程度（由簡到繁）依次為：位移圖像法（因直接利用實驗測定量的位移和時間，故位移圖像法最簡捷）、變形中時速度圖像法、變形速度圖像法、基本中時速度圖像法、基本速度圖像法、線性化圖像法.因此，更宜采用位移圖像法處理打點紙帶測定加速度.這就為圖像法的層次性、開放性實驗教學設計奠定了堅實的物理理論基礎.

5.2 圖像法與逐差法的比較

圖像法、逐差法均是擬合直線或曲線的方法，也是數據處理的基本方法.［5］作圖圖像法的實質是粗略平均法，回歸圖像法的實質是數理統計法即最小二乘法；逐差法的實質是差分－平均法.一般而言，逐差法的處理結果比作圖圖像法的精確，與回歸圖像法的相差不大；［5］或原則上，逐差法的標準差比回歸法的大.［7］因此，對處理打點紙帶測定加速度、初速度而言，回歸圖像法最精確、逐差法次之、作圖圖像法最次.

雖然如此，作圖圖像法仍不失為中學物理實驗基本訓練的數據處理方法，逐差法是中學物理實驗合理、實用的數據處理方法，回歸圖像法可作為中學物理實驗提高、開放的數據處理方法.

6 結語

本文拓展了處理打點紙帶測定加速度、初速度的圖像法；從作圖工具和物理實驗教學探討了圖像法的分類，提出了作圖圖像法和回歸圖像法；提供了推證的12種回歸圖像法運用的一個典型實例；比較了各圖像法的特點、簡捷程度；討論了作圖圖像法、逐差法、回歸圖像法的精確程度、中學物理實驗的適用情形.

圖像法不僅是物理實驗的數據處理方法，而且是物理實驗的基本內容.因此，本文的研究既可作為關于數據處理方法的高中物理課程資源，又可作為物理學科學方法教育的顯性方法的內容，是高中物理教師深入認識、教學設計打點計時器實驗的物理基礎；同時體現了高中物理課程內容理念的基礎性、選擇性、時代性（回歸圖像法作為回歸法與計算機的計算、圖像功能相結合的方法在高中物理教科書［8］中業已呈現），高中物理課程實施理念的多樣性，并突出了開放性.可以預見，通過本文推證的處理打點紙帶測定加速度、初速度的圖像法的探究式教學，可很好地培養物理實驗的數據處理方法，可更好地理解勻變速直線運動的規律，進而提升物理實驗的數據處理能力.

1 許國梁，束炳如.中學物理教學法（第2版）.北京：高等教育出版社，1993.358

2 陶洪.物理實驗論.南寧：廣西教育出版社，1996.185，188

3 王興乃，羅棟國.高中物理實驗大全（第1冊）.北京：電子工業出版社，1989.166－167，179－181，186－188

4 安忠，劉炳升.中學物理實驗教學研究.北京：高等教育出版社，1986.185—187

5 龔鎮雄.普通物理實驗中的數據處理.西安：西北電訊工程學院出版社，1985.88—89，80—82，95—96，122，132

6 朱鶴年.基礎物理實驗教程：物理測量的數據處理與實驗設計.北京：高等教育出版社，2003.59－60，68－69

7 朱鶴年.新概念物理實驗測量引論：數據分析與不確定度評定基礎.北京：高等教育出版社，2007.80

8 人民教育出版社課程教材研究所，物理課程教材研究開發中心.普通高中課程標準實驗教科書·物理1（第2版）.北京：人民教育出版社，2006.32