混響噪聲局部平穩條件下次佳檢測方法研究*

余義德，劉 欣，李全瓊

(91550 部隊，大連 116023)

1 引言

在東海海域沉底小目標的海底主動探測中，發現混響是回波信號的主要干擾，給探測圖像的判讀帶來一定困難。因為混響是發射信號作用于海底后，在回波信號接收面上由大量散射體的散射波疊加形成的，所以混響與發射信號是強相關的，具有在時域上難分離，在頻域上又極其相似的特點。有研究表明［4］，海底小目標散射體尺度的不均勻性，現代基陣的大孔徑、窄波束和寬頻帶特性都使得等效散射體的數量變少，導致混響信號的瞬時值偏離高斯分布，成為非平穩的有色信號。一般來說，匹配濾波器對于高斯白噪聲背景是最佳檢測器，能得到最大的輸出信噪比，但混響的非平穩性和有色性導致在高斯分布假設條件下的最佳檢測器性能大大降低［1，8］。基于此，數據在送入匹配濾波器前，應當先級聯一個“白化濾波器”［2］，通過對混響信號的預白化處理，實現混響背景下的信號次佳檢測。

根據實際發射信號長度和混響信號特點將接收信號分段，基于混響信號的局部平穩性結論，利用當前數據段的AR 模型系數對下一數據段進行白化處理，實現了混響背景下的信號檢測問題。目前，該方法已經成功應用于東海海域沉底小目標探測中。

2 方法的提出

2.1 混響信號的局部平穩性驗證

預白化需要噪聲的譜信息，由于混響噪聲的強非平穩性，它的協方差函數不可能僅僅通過單一信號估計出來［3］，但是，一般由于發射信號的脈寬很小，可以近似認為混響在此脈寬時間段內是局部平穩的，進而可以通過分段白化對信號進行檢測。首先對于聲納工作的東海海域經典混響信號應用“CLR 統計距離法”對其是否滿足局部平穩性進行驗證［6］。截取試驗中的一段混響數據，計算它的GLR 距離。試驗中發射信號的中心頻率為32.5KHz，信號帶寬為15KHz，脈寬為4ms的線性調頻信號。信號的時間波形及相應的GLR 距離如圖1所示。可以看出，混響數據在時間上是非平穩的，隨著時間的增加，GLR 距離增大，即兩段信號的譜特性差異變大，但是混響數據在發射信號脈寬的量級上，滿足局部平穩性，相鄰兩段之間的譜距離比較小，譜特性較為相似，可以認為混響信號滿足局部平穩性。

2.2 信號預白化檢測方法

信號分段預白化的方法是:利用前一段數據建模形成的白化濾波器對后一段數據進行白化，然后進行匹配濾波。即利用前一段數據所估計的AR 模型參數α 和階數P 構造白化濾波器，對后段分塊數據進行濾波，將混響濾波成為白噪聲，最后再進行相關檢測處理。如圖2 所示，首先進行信號分段，如果第K 段沒有信號，用第K 段的協方差信息估計出濾波器對第K+2 段噪聲白化，在第K+2 段高斯白噪聲背景下對信號W(s(t))進行最佳檢測，如果沒檢測到有信號，增加K，回到第2 步，若檢測到有信號，則可進行下一階段的匹配濾波。

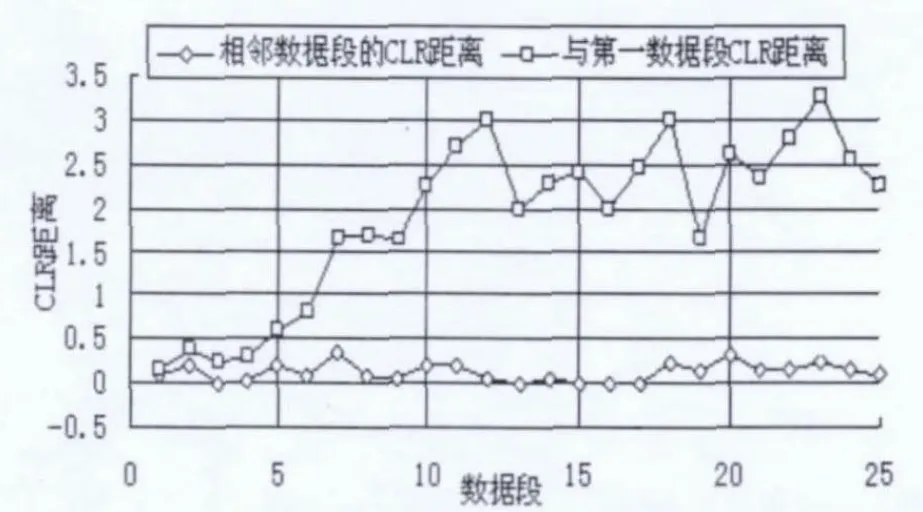
圖1 數據分段示意圖

圖2 混響背景下的次佳信號檢測流程

2.3 白化濾波器模型［9－10］

3 關鍵參數確定

3.1 數據分段

數據分段長度直接影響白化濾波器的效果［5］。假設在觀測時間T 內水聽器接收的信號x(t)中有回波信號s(t)，s(t)的脈寬為TP，時延為τ(τ為一未知常數)。考慮將x(t)分為寬度為TB的數據段，數據分段的基本原則是:數據段寬度TB必須與需檢測信號的脈寬TP相當，s(t)的寬度必須小于數據段的寬度，即TB＞TP，s(t)必須完全位于數據段#2 中，即ΔT≤TB－TP。采用的數據分段方案是:取數據段的長度為發射信號長度的兩倍，相鄰兩數據段之間有二分之一重疊，如圖3 所示。

3.2 模型參數的確定

在預白化過程中AR 模型階數p的確定和系數a的估計是方法的核心，直接影響最終的系統檢測性能。階數p的確定與數據分段長度有關，可以通過MDL 準則得到。由于受到實際混響非高斯特征的影響，無法用信號的高階統計量進行有效估計。采用基于三階累積量的高階譜估計方法對參數a 進行估計［7，11］。假設x(t)的三階累積量:

且滿足:

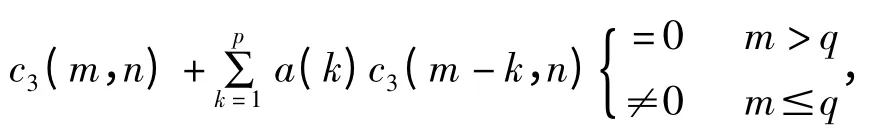
其中，p，q 分別是模型AR 和模型MA的階數。

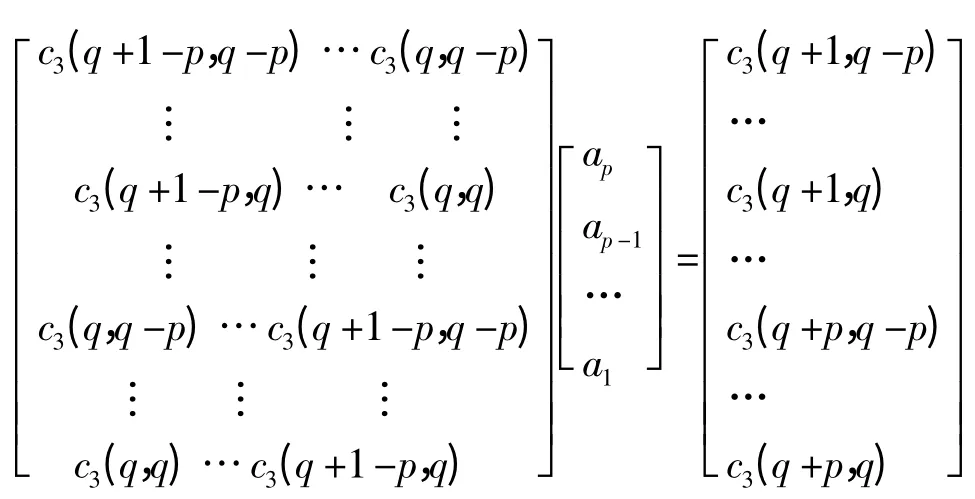
通過對方程求解，可以得到參數a的估計值。

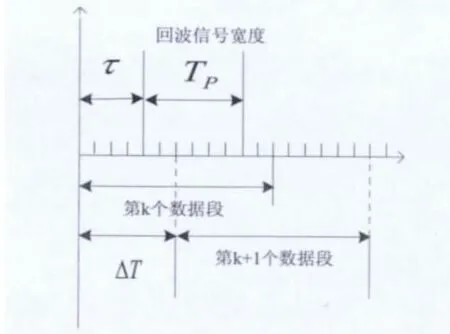
圖3 GLR 統計距離隨分段號的變化

4 仿真分析

仿真數據為純海底回波采集回來的混響數據，發射的信號為線性調頻信號，發射信號的周期為1s，發射信號的脈寬為0.5ms，信號頻率為15KHz－30KHz，采樣頻率為500KHz，截取混響數據的長度為10000個點，目標回波信號加在5000個點的位置，信混比為－13dB。數據分段采取1/2 重疊原則，每一段數據的長度為發射信號長度的兩倍。數據采用常規方法和預白化方法處理的結果如圖4 所示。

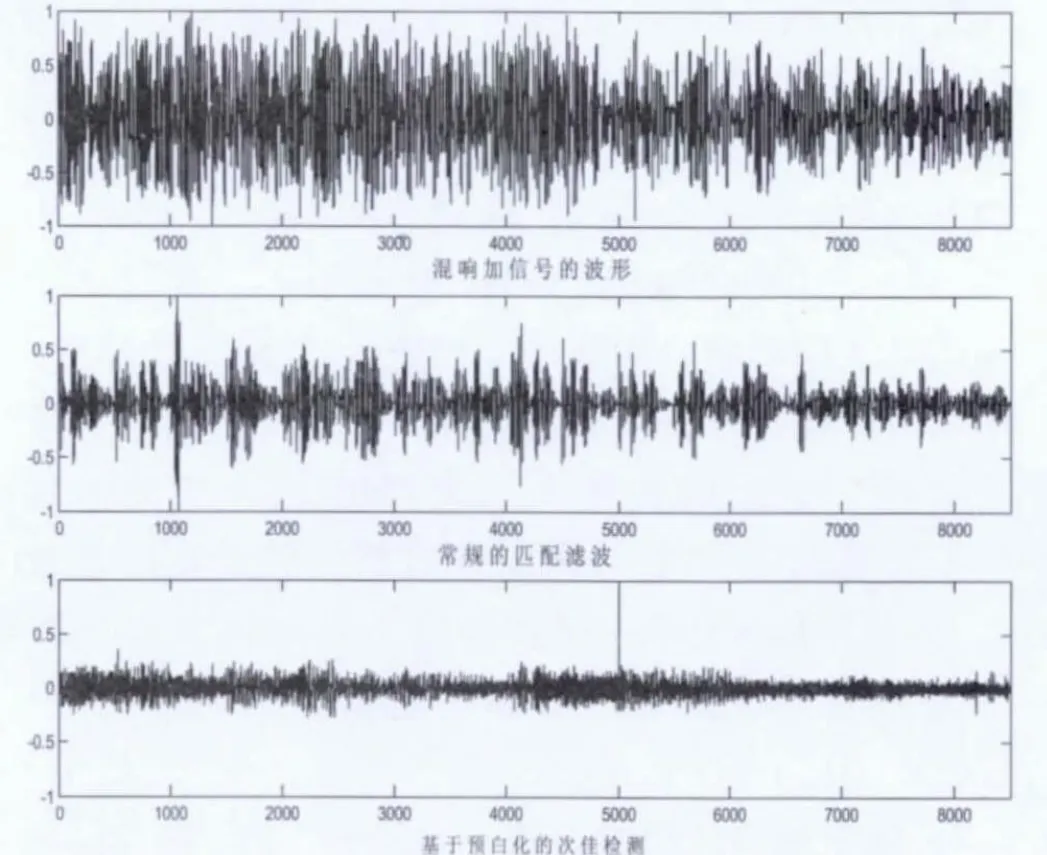
圖4 信號的原始波形及兩種不同方法的檢測結果

5 實驗驗證

由于實際試驗數據目標的回波信號比較弱，想要檢測出來比較困難，先對不同基元的接收數據進行波束形成，對波束形成后的數據再進行上述的分段預白化檢測，其結果如圖5 所示。可以看出，對于實驗數據，基于局部平穩的次佳檢測較常規的匹配濾波而言能獲得一定的信混比增益。

6 結論與展望

對于文中的混響信號，基于局部平穩的預白化次佳檢測較常規的匹配濾波而言，在檢測性能上有所改善，仿真結果優于實驗結果。這是由于實際檢測結果很大程度上依賴數據分段的情況，而且在用AR 模型預測的時候，在相鄰兩段數間存在一定的數據不連續性，易產生尖峰脈沖，因此這種算法具有一定的不穩定性，并且易受分段的影響，這也是下一步深入研究的方向。

［1］肖先賜.現代譜估計:原理與應用［M］.哈爾濱:哈爾濱工業大學出版社，1989:30－35.

［2］王玉泉.水聲設備［M］.哈爾濱:哈爾濱工程大學出版社，1999:234－237.

［3］張賢達.現代信號處理［M］.北京:清華大學出版社，2002:74－103.

［4］朱廣平，孫輝，陳文劍.混響背景中信號檢測的特征核支持向量機［J］.哈爾濱工程大學學報

［5］吳國清.自適應分段技術在回波分析中的應用［J］.應用聲學，1985(4):23－31.

［6］趙航芳，祝獻，宮先儀.混響背景下信號的檢測［J］.哈爾濱工程大學學報，2004(25):34－37.

［7］薛山花，田杰，李宇，等.基于時變AR 預白濾波處理的水雷非水雷識別算法［J］.微計算機應用，2008，29(2):2－5.

［8］D.A.Abraham，A.P.Lyons.Reverberation envelope statistics and their dependence on sonar beamwidth and bandwidth in Impact of Littoral Environmental Variability on Acoustic Predictions and Sonar Performance［J］.N.G.Pace and F.B.Jensen Eds.Norwell MA:Kluwer，2002:539－546.

［9］Cannillet V，Joulain G.Wideband sonar detection in reverberati on using autoregressive models［J］.Proc Oceans＇96 MTSIIEEE，Fort Laud.Erdale，1996 (3):1435－1440.

［10］Carmillet V，Amblard Po.Detection of phase－ or frequency－ modulated signals in reverberation noise［J］.JASA，1999(6):3375－3389.

［11］李全瓊.高分辨率聲納海底混響統計特性分析及抑制技術研究［D］.哈爾濱:哈爾濱工程大學，2009.