試論彈性碰撞的條件

程旭健

（武義二中，浙江 武義 321203）

彈性碰撞（又稱完全彈性碰撞）是中學物理和大學物理中都涉及的課題.彈性碰撞的特點是碰撞前后兩物體的總動量和總動能守恒.那么，彈性碰撞成立的前提條件是什么？

17世紀，惠更斯指出，只有在碰撞后物體不發(fā)生永久形變、不裂成碎塊、不粘在一起、不發(fā)熱以及不發(fā)生其他內(nèi)部變化的情況下，動能才是守恒的.這個表述是具體的，直觀的，但不夠深入.

現(xiàn)在一般大學教材論述彈性碰撞的過程時，把它分為兩個階段：壓縮階段和恢復階段.兩物體碰撞壓縮時有一部分（或全部）動能轉(zhuǎn)化為彈性勢能，在恢復階段彈性勢能全部變回動能.據(jù)此，有的文獻提出了不妥當?shù)恼f法.如網(wǎng)上百度百科這樣定義彈性碰撞：兩碰撞體的接觸區(qū)域僅發(fā)生彈性變形的碰撞表述為：“真正能反映碰撞過程的定義應當是：如果兩球碰撞過程中相互作用的內(nèi)力完全是由于形變引起的彈性力（保守力），而無其他非保守內(nèi)力的作用，則此碰撞稱為完全彈性碰撞.”［1］

僅發(fā)生彈性形變的碰撞就是彈性碰撞嗎？筆者認為，兩個彈性體碰撞過程中相互作用的內(nèi)力完全是由于形變引起的彈性力（保守力）的前提下（沒有產(chǎn)生內(nèi)能或塑性形變之類），這種碰撞還未必是彈性碰撞.因為碰撞過程中一般有部分動能轉(zhuǎn)化為彈性勢能，所以動能并不守恒，只能稱為機械能守恒，即動能與彈性勢能之和守恒，稱不上彈性碰撞.現(xiàn)分析和計算如下，不妥之處請指正.

對于最簡單的模型如兩個帶小球的彈簧碰撞見圖1，動能是守恒的，但對結構稍復雜一點的物體，碰撞結束后，物體未必恢復原狀，因而保留有一部分彈性勢能，這部分彈性勢能和動能相互轉(zhuǎn)化，也就是說，物體碰撞結束之后還會振動.圖2所示的兩個鋼球碰撞時有清脆的撞擊聲；碰撞彈開后我們試著用手抓住其中任一個鋼球，手會感到有振顫感.這些事實說明物體碰撞后有一部分動能轉(zhuǎn)化成振動的能量.

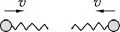
圖1

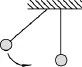
圖2

為簡單起見，我們考慮這樣一個物理模型如圖3：碰撞的兩物體是對稱的，每個物體都由兩個小球和兩根彈簧聯(lián)結起來，碰撞速度大小一樣.由于對稱性，它們的碰撞點（接觸點，稱為O點）是靜止的.在碰撞結束前它們一直接觸，這段時間內(nèi)可以看作固定在O點，這樣就把一個碰撞問題轉(zhuǎn)化為彈性振動問題.為此建立坐標系如圖4，x1、x2代表兩小球偏離平衡位置的位移.建立該系統(tǒng)的振動微分方程（忽略小球與水平支承面之間的摩擦）.

圖3

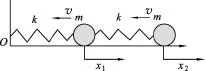
圖4

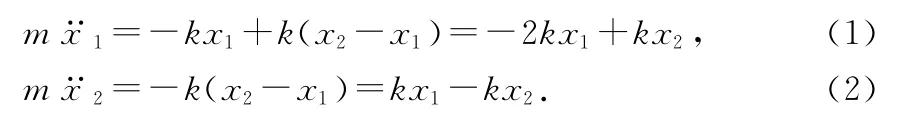
寫成矩陣形式

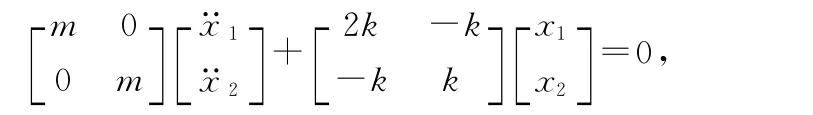
即

上式中

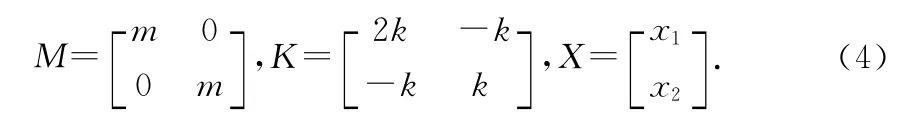
據(jù)文獻，［2］上述方程有非零解的充分必要條件是

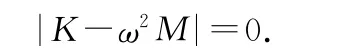
將具體值（4）代入，求得

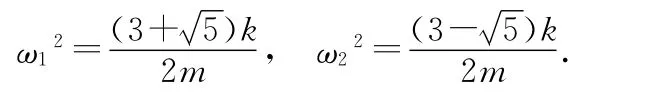
設特解x1＝Asin（ω1t＋φ1），x2＝Bsin（ω1t＋φ1），代入方程（1）、（2），求得

設特解x1＝Csin（ω2t＋φ2），x2＝Dsin（ω2t＋φ2），代入方程（1）、（2），求得則設一般解為

代入（5）式，得

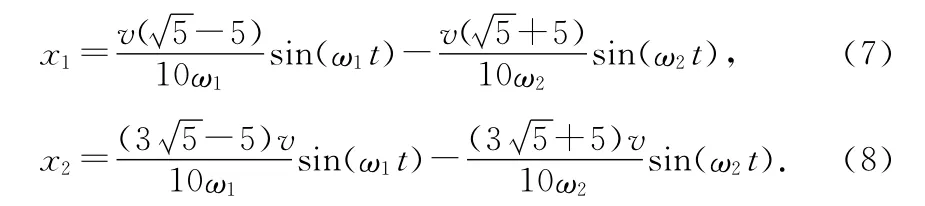
x1的兩個分量都是周期函數(shù)，x1開始時為0，經(jīng)過一段時間，再次為0時，左邊第一根彈簧由壓縮狀態(tài)恢復原長，接下去x1變?yōu)檎担磸椈蓪㈦x開原點，意味著碰撞結束，算出此時物體的動能，與初始動能比較，就可以知道是否動能守恒.

對上述方程用天空軟件站的圖像繪制軟件《冰竹之新數(shù)學函數(shù) 參數(shù)方程》按精確到小數(shù)點后4位求得時，第2次x1＝0.此時

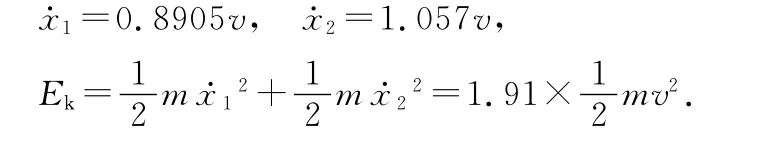
而初始動能是

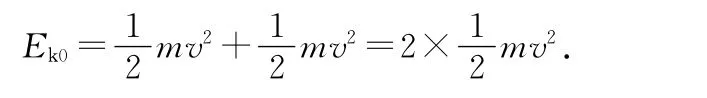
筆者再次用上述軟件按精確到小數(shù)點后7位重新計算，得

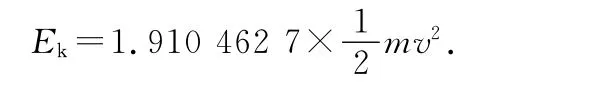
可見以一個小球和一根彈簧聯(lián)結而成的物體在對稱碰撞后確實動能不守恒，有一小部分動能（大約4.5%，即由算出）轉(zhuǎn)化成彈性勢能.

上面的精確計算表明，一般彈性體碰撞結束后動能不守恒，有一小部分動能轉(zhuǎn)化為彈性勢能，所以不等于彈性碰撞.彈性碰撞是一種理想化的物理模型，除了要求碰撞過程中相互作用的內(nèi)力完全是由于形變引起的彈性力（保守力）外，還要求碰撞物體剛度大（即變形小）、幾何尺寸小，從而碰撞時間短，碰撞作用瞬時傳到整個物體，這樣的宏觀物體的碰撞才可近似地看作是彈性碰撞.真正的彈性碰撞，只有在分子、原子以及更小的粒子之間才會遇到.

1 李增林等.力學.南京：南京工學院出版社，1988.197—203

2 中山大學數(shù)學力學教研室.力學教程.北京：高等教育出版社，1978.277—288