基于半徑變化量測量的圓度誤差最小外接圓評定法研究

張玉梅

（赤峰學院建筑與機械工程學院，內蒙古赤峰024000）

基于半徑變化量測量的圓度誤差最小外接圓評定法研究

張玉梅

（赤峰學院建筑與機械工程學院，內蒙古赤峰024000）

最小外接圓法是一種工程中常用的圓度誤差評定方法.文章給出了基于半徑變化量測量的圓度誤差最小外接圓評定法的數(shù)學模型和最小外接圓的判定方法和條件.實驗結果表明，給出的數(shù)學模型是正確的，判定條件是合理可行的.

最小外接圓法；半徑變化量測量；圓度誤差

1 前言

根據(jù)國家標準GB/T7235-2004，圓度誤差主要有四種評定方法，分別是最小區(qū)域圓法、最小二乘圓法和切接圓法（包括最小外接圓法和最大內接圓法）[1].其中最小外接圓法是工程中常用的一種方法，主要用于軸類零件的圓度誤差評定，相當于基孔制的軸孔配合情況[2].

按采樣方式不同，圓度誤差的精密測量有坐標測量法和半徑變化量測量法[3].本文將在最小二乘圓法的基礎上，研究基于半徑變化量測量方式的圓度誤差最小外接圓評定法的數(shù)學模型，討論最小外接圓的判定條件.

2 最小外接圓法圓度誤差評定數(shù)學模型

最小外接圓法圓度誤差評定數(shù)學模型在最小二乘圓法基礎上給出.

所謂最小二乘圓法，是指根據(jù)實際被測輪廓上各測量點到最小二乘圓的徑向距離平方和最小的原則，首先確定最小二乘圓，據(jù)此確定的圓度誤差值等于實際被測點到最小二乘圓的徑向距離最大值（正）與最小值（負）的差值，如圖1所示.

根據(jù)文獻[3]，基于半徑變化量測量的最小二乘圓圓心坐標O0(x0，y0)和最小二乘圓半徑R0分別為：

式中M表示測量一周的采樣點數(shù)；

j表示采樣點序號，j=1,2,…,M；

r0表示第一個測量點至回轉中心的距離；

ΔRj表示任一測量點相對于第一個測量點的半徑變化量.

θj表示任意測量點與第一個測量點間的夾角；

任意測量點Pj相對最小二乘圓的徑向偏差值δj為：

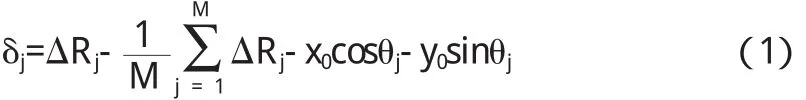
最小二乘圓法評定的圓度誤差E0的數(shù)學模型為：

式中ΔRmax，ΔRmin分別表示實際被測點到最小二乘圓的最大偏差值點和最小偏差值點相對于第一測量點的半徑變化量；

θmax，θmin則表示與ΔRmax，ΔRmin相對應的測量點角坐標.

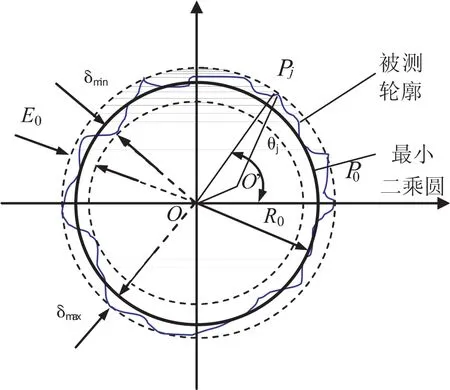
圖1 最小二乘圓法圓度誤差評定原理圖

最小外接圓法的評定過程是：先作實際被測輪廓的最小外接圓，然后作與最小外接圓同心的被測輪廓的最大內包容圓，兩同心圓的半徑差，就是最小外接圓法評定的圓度誤差，如圖2所示.O1是最小外接圓圓心，R1是最小外接圓半徑，Rmin是與最小外接圓同心的被測輪廓最大內包容圓的半徑，即被測點中到最小外接圓徑向距離最大點所對應的半徑.按此方法評定圓度誤差E1計算式為：

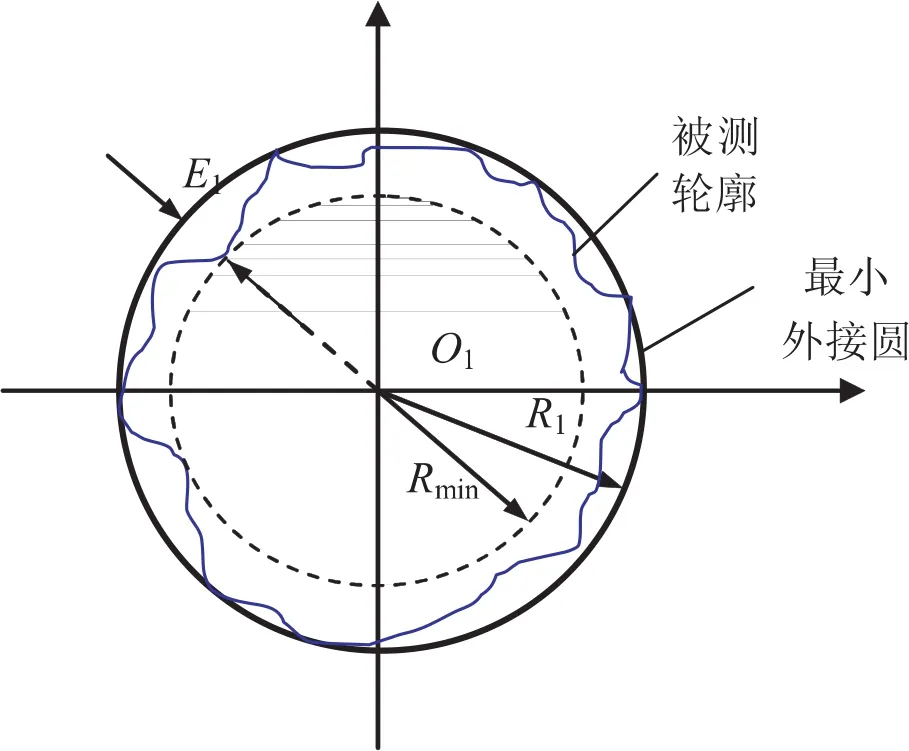
圖2 最小外接圓法圓度誤差評定原理圖

按照確定最小二乘圓的方法，加上最小外接圓的判斷條件來確定最小外接圓，得到基于半徑變化量測量的最小外接圓法圓度誤差評定數(shù)學模型為：

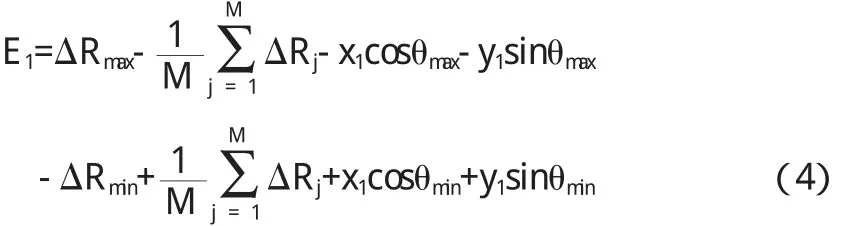
式中M、j、ΔRj同上；

(x1,y1)表示最小外接圓的圓心坐標；

ΔRmin表示位于同心最大內包容圓上的測量點的半徑變化量測量值；

θmin表示與ΔRmin相應測量點的角坐標值.

ΔRmax表示位于最小外接圓上的測量點的半徑變化量測量值；

θmax表示與ΔRmax相應測量點的角坐標值；

根據(jù)文獻[4]，最小外接圓的判斷準則有兩種，分別為：

（1）對徑準則.外接圓與被測輪廓兩點相接，且此兩點連線為外接圓直徑.

（2）三角形準則.外接圓與被測輪廓三點相接，此三點相連后形成銳角或直角三角形.

測量點屬于外接圓和被測輪廓接觸點的判斷方法是：被測沾到最小二乘圓偏差值最大且相等.

基于半徑變化量測量的最大偏差值計算式為：

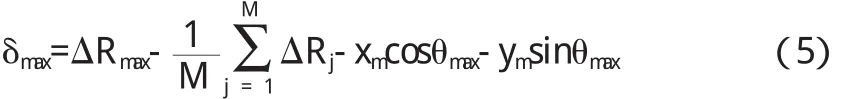
式中(xm,ym)表示外接圓圓心坐標.

3 最小外接圓判定方法

3.1 對徑準則的判定方法

若被測點中有兩點（A和B）與最小二乘圓的徑向偏差值最大且相等，即

同時，此兩點的角坐標滿足式（6），

則判斷此圓是最小外接圓.否則，按下面方法進行判斷.

3.2 三角形準則的判定方法

若被測點中有三點（A、B和C）與最小二乘圓徑向偏差最大且相等，即

則首先將三點的角坐標θA，θB，θC按由大到小的順序排列，比如θA>θB>θC，然后按照下列條件判斷是否滿足銳角或直角三角形準則.

條件1若θA-θC=180°，則A、B、C三點連線會構成直角三角形，如圖3所示（設θC=0°），說明此時的外接圓是最小外接圓.

圖3 三角形準則最小外接圓判定條件1

條件2：若同時成立，則A、B、C三點連線構成銳角三角形（如圖4（a））或直角三角形（如圖4（b））（設θC=0°），可以判定此外接圓為最小外接圓.

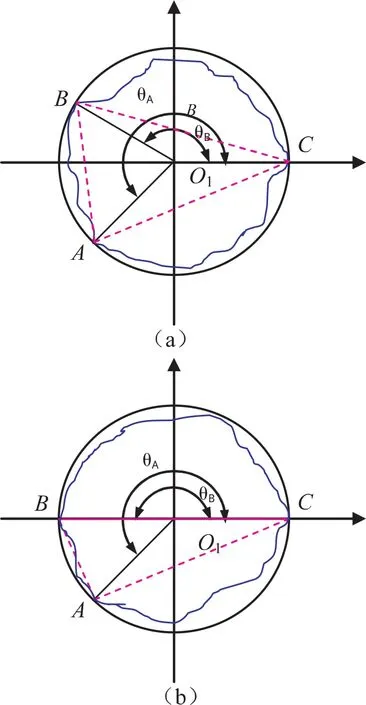
圖4 三角形準則最小外接圓判定條件2

條件3若θA-θC<180°，如圖5所示（設θC=0°），說明A、B、C連線會構成鈍角三角形，則說明此外接圓不是最小外接圓.

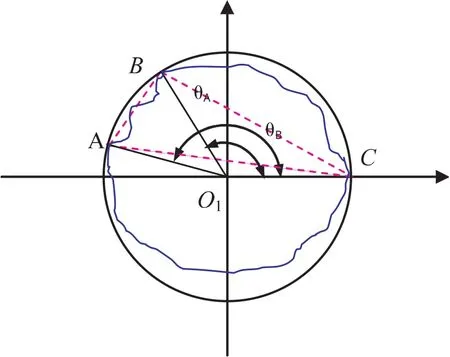
圖5 三角形準則最小外接圓判定條件3

條件4若θB-θC>180°，如圖6所示，（設θC=0°），說明A、B、C連線構成鈍角三角形，說明此外接圓不是最小外接圓.

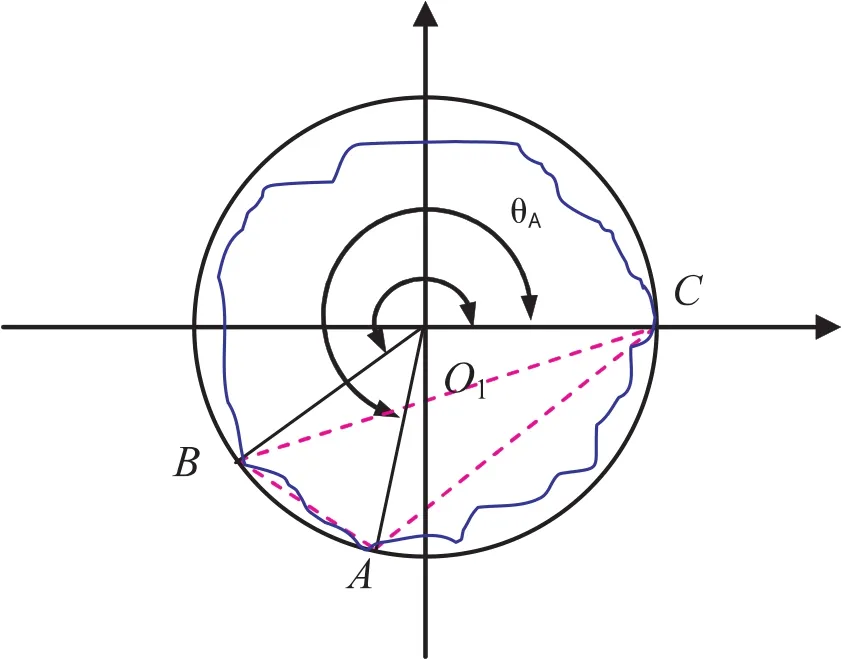
圖6 三角形準則最小外接圓判定條件4

最小外接圓判定條件匯總結果見表1.

表1 最小外接圓判定條件

3.3 最小外接圓與被測輪廓接觸點數(shù)多于三點時的判定方法

當外接圓和被測輪廓接觸點數(shù)量超過三點時，將所有接觸點的角坐標排序，三個一組，按一個方向逐次判斷.只要出現(xiàn)一組滿足表1所列最小外接圓成立條件即可.

4 實驗驗證

將圓度誤差的半徑變化量測量數(shù)據(jù)，經(jīng)過濾波等數(shù)據(jù)處理后，得實際輪廓，再根據(jù)前文給出的圓度誤差最小外接圓評定法數(shù)學模型和最小外接圓判定條件，通過優(yōu)化算法得到最小外接圓，結果如圖7所示.A、B、C三點滿足三角形準則中的判定條件2.

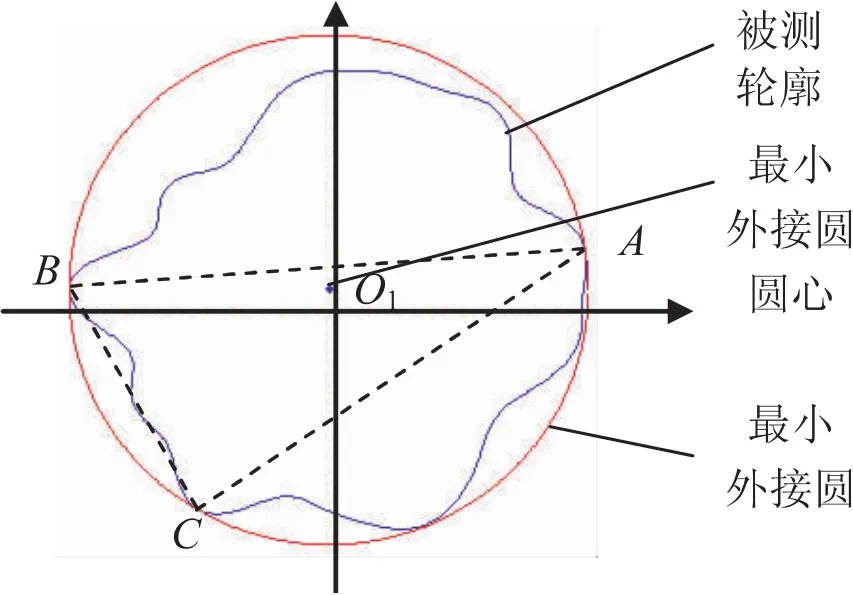
圖7 被測輪廓與最小外接圓

5 結論

針對圓度誤差的半徑變化量測量法，研究了工程中常用的圓度誤差最小外接圓評定法的數(shù)學模型，并給出了最小外接圓的判定條件.實驗結果表明，給出的基于半徑變化量測量的圓度誤差最小外接圓評定法的數(shù)學模型是正確的，最小外接圓的判定方法和條件是合理可行的.研究結果對基于半徑變化量測量的圓度誤差評定方法研究有重要的應用價值.

〔1〕GB/T7235—2004,產(chǎn)品幾何量技術規(guī)范(GPS)評定圓度誤差的方法[S].中華人民共和國國家質量監(jiān)督檢驗檢疫總局，2004.

〔2〕方沁林.圓度誤差評定的算法研究與軟件設計[D].武漢:華中科技大學,2007.

〔3〕甘永立.形狀和位置誤差檢測[M].北京:國防工業(yè)出版社，1995.

〔4〕曹麟祥,王丙甲.圓度檢測技術[M].北京:國防工業(yè)出版社，1998.

TB92

A

1673-260X（2013）11-0013-03