最短路算法及其在物流管理中的應用

余麗

（肇慶醫學高等專科，廣東肇慶526020）

最短路算法及其在物流管理中的應用

余麗

（肇慶醫學高等專科，廣東肇慶526020）

本文介紹了最短路的兩種算法，并介紹了它們在物流管理中的若干應用.將Dijkstra算法與Floyd算法用于解決物流管理中的配送路徑問題以及配送中心選址問題，并對這兩種算法進行比較.

Dijkstra算法；Floyd算法；最短路

1 引言

最短路問題是交通網絡分析中的一個重要的問題，它是資源分配、路線設計及分析等優化問題的基礎.給定一個網絡，如何求它從某點到其它點的最短路，或者如何求任意兩點間的最短路?對此，已有很多好的算法.

最短路算法在物流管理中有廣泛的應用.物流業被人們看作是世紀經濟發展的新領域，在大力發展物流的同時,人們面臨著一個共同的問題：即物流配送中心如何進行合理的選址，如何選擇合適的配送路徑.物流中心選址及配送路徑的選擇是否合理直接關系到企業各項經營成本及其獲利程度.因此，合理選擇物流配送中心及配送路徑對于物流系統的規劃至關重要.而最短路算法正可以為物流配送中心選址及配送路徑選擇提供強有力的理論支持.

2 最短路算法

2.1 Dijkstra算法

Dijkstra算法是一種通過源結點出發到網絡當中其他的地方各個點，從中尋找最佳的路徑和最短的通路的著名的算法.目前，Dijkstrs算法是大部分系統在解決最短路徑的問題時所應用的理論基礎，不同的系統對這種算法采用的時候實現的方式也是不同的.總的來說，該算法其主要的思想就是從源結點出發，按照路徑的長度的遞增次序，每一次找一個結點跟源結點之間的最短通路，然后不斷繼續地尋找，直至把全部的結點找到為止，因此就產生了最短路徑.

Dijkstra算法的基本思想如下：

Dijkstra算法的基本思想是從圖G中的n-1個獨立割集中的每一個都選取一條最小的邊，從而構成一個最小樹.現敘述如下：設圖G的點綜合為（x={1,2,3,…,n}），邊eij的權為wij.

第1步置u1=0，uj=w1j，j=2，3，…，n，P={1}，T={2,3,…, n}；

第2步在T中尋找一點k，使得

置P=PU{k}，T=T-{k}.若T=?，終止；否則，進行第3步.

第3步對T中每一點j，置uj=min{uj，uk+wkj}，然后返回第1步.

該Dijktra算法其實就是在保證局部距離的最短來更好地獲得整體距離最短，是一種以局部來計算總體的貪心的策略的算法.如果從源點到其中任意點的路徑不存在，那么可以假設該點的最短路徑是一條長度為無窮大的虛擬路徑.通過這個的分析，我們可以知道Dijkstra算法過程是由沒有被確定為最短路徑頂點的全部頂點中選擇出一個權值最小的弧段，直至對比得到這一點頂點為止，然后仍舊不斷地繼續前面相同的工作，不斷地反復循環.

Dijkstra算法在計算任意一個點到其他的點的最短路徑的時候一共需要兩次的循環，其時間的復雜度是O(n2).因此在計算一對頂點之間的最短路徑的時候，需要以每一個頂點作為源點.如果執行算法n次，那么總的執行的時間的復雜度是為O(n3)，所以要選擇一個弧段是權值是最小的話，就必須把全部還沒確定的頂點都來掃描一次，如果數據量比較大的話，就會對計算機的速度產生較大的影響.

2.2 Floyd算法

Floyd算法又稱為弗洛伊德算法，插點法，是一種動態規劃的算法，用于尋找給定的加權圖中頂點間最短路徑的一種算法.Floyd算法在所以頂點之間的最短路徑的算法中是很具有代表性的，其核心的思想是通過一個圖的權值矩陣求出它的每兩點間的最短路徑矩陣.每次迭代求出的是只經過點集的某個子集的最短路徑（一般來說初始矩陣就是鄰接矩陣），這個子集在每次迭代中都加多一個點，當全部的頂點都作為中間頂點的時候，就可以求出最后的權矩陣，這時就反映出全部的頂點之間的最短的距離.

其算法思路如下：單獨一條邊的路徑也不一定是最佳路徑.從任意一條單邊路徑開始.所有兩點之間的距離是邊的權的和，(如果兩點之間沒有邊相連,則為無窮大）.對于每一對頂點u和v，看看是否存在一個頂點w使得從u到w再到v比己知的路徑更短.如果是更新它.不可思議的是，只要按排適當，就能得到結果.dmij為從節點i到節點j的最短距離.

3 最短路算法在物流管理中的應用

隨著經濟的全球化迅速發展和信息科技技術的突飛猛進，物流的配送技術也隨著迅速提升.物流配送與我們先進的信息科技技術以及數學模型的工具也是息息相關，緊密地結合在一起，通過應用各種優化的方法對物流配送當中的各個環節進行管理，甚至進行決策，從而實現了最佳的配合.同時，最短路算法在物流配送中能夠適應現代物流的特點，可以達到減少成本和提高經濟效益和物流效益的效果.

3.1 最短路算法中物流配送路徑的選取中的應用及算法比較

例1現有一批食品，打算由v1汽車站配送到v5大型超市，尋找一條最短的路線.經過實際測量，得到以下路線網絡圖，如圖1所示.

圖1

3.1.1 用Dijkstra算法計算

（1）求出v1到v2的最短距離為1千米，v1到v2的最短距離為2千米，v1到v4的的最短距離為∞千米，v1到v5的最短距離為∞千米.由于v1到其他各距離最小為1，所以保留邊e12.

（2）仍用Dijkstra算法計算v2到v3、v4、v5的距離；取(ui,u2+w2i)，保留該點以及之前的點和邊.

（3）重復進行之前一步，直到找出最短路徑為止.迭代過程如下：

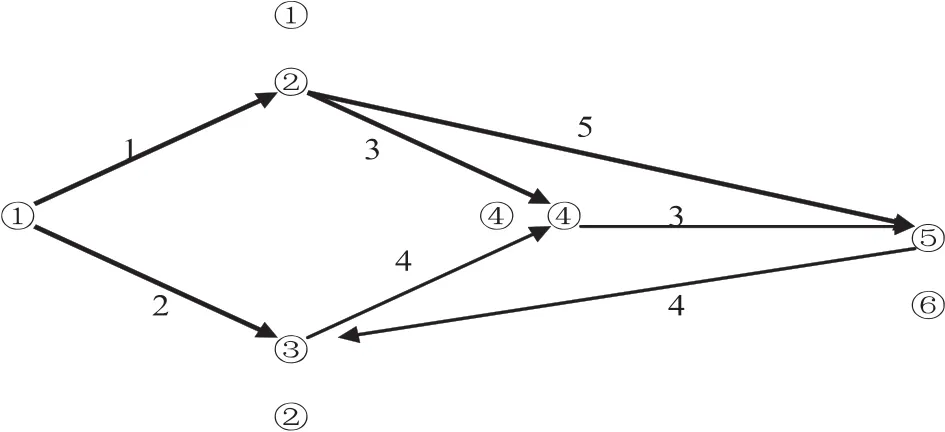
根據上面的步驟，可以得到從v1汽車站配送到v5大型超市的最短路徑長度為6，即走v1v2v5.

3.1.2 用Floyd算法計算

Floyd算法主要用距離矩陣來求解，所以先要構造n個矩陣D0，D1，…Dn.本例中n=5，從D5矩陣中可以直接讀出到相互之間的最短距離.

根據Floyd算法來解題,如下：

第一步:確定矩陣D0.如果頂i和j之間有邊相連等于該邊長度，如果沒有.由圖2可知

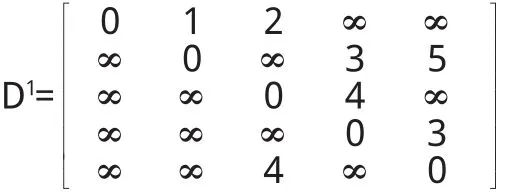
第三步：采用類似的辦法可得D2,D3,D4,D(5)矩陣為:

D5的各元素值就是相應頂點間的最短路徑.D5矩陣中對應的就是v1到v5相互之間的最短距離，顯然可以看出兩地之間的最短路徑長度為6.

通過上面的例子可以了解到：Dijkstra算法通常用在計算一個點到其他的點之間的最小的路徑，它在搜索的過程中，剛好與物流系統當中由一個中心點到其他點從近到遠的配送方式一致：雖然Flody算法是求出每兩個點間的最短的路徑，可是它僅僅是求出兩點間的最短路徑的長度，卻未能對整個路徑的結點作標示，這對物流配送查詢途徑路徑造成困難.兩者相比之下，Dijkstra算法的性能較為穩定，同時也比較適合網絡的拓展變化，因為選擇Dijkstra算法為物流配送運輸路線的基礎算法.

3.2 基于最短路算法的物流中心選址方法

本文中最短路算法包含Dijkstra算法和Flody算法，也就是頂點對間的最短路的算法和全部頂點之間的最短路算法.Dijkstra算法在物流的配送運輸中能夠合理的進行決策和分析，而Flody算法比較適合選擇合理的物流中心，從而使物流的總費用達到最少的效果，但是在選擇物流中心時，由于一些約束的條件限制，導致選擇物流位置只能在特定的一些區域，同時，物流運輸的費用與物流運輸的距離呈非線性的關系.

下面結合實例來說明最短路徑說法在物流配送中心選址中的應用.

例2已知定點①、②、③、④,各點間的費用如圖2所示，在四個點中選定一個點為物流的中心，使得該點到其他每個點的費用是最小的.

圖2

3.2.1 根據Dijkstra算法來解題,如下：

反復應用Dijkstra算法，求出每一個候選地到其它各點的最短路徑，由于過程較多，只給出如下結果：

利用Dijkstra算法，得到上面的結果，通過觀察可以得出①到②的最短距離為1，①到③的最短距離為2，①到④的最短距離為3，由此，①到②、③、④各點最短距離和為6同理，②到其它處最短距離和為11，③到其它處的最短距離和為9，④到其它處的最短距離和為6.比較各處到其它各處費用和的大小，可知①和④處到其它各點的費用最小.因此，①和④處就經濟要素而言是最優的.

3.2.2 根據Floyd算法來解題，如下：

第一步：確定矩陣D0.如果頂i和j之間有邊相連等于該邊長度，如果沒有，而.由圖4可知

由此可知

第三步：采用類似的辦法可得D2，D3，D4矩陣為

D4的各元素值就是相應頂點間的最短路徑.第一行值之和即為①處到其它三處的物流費用的和，可知①到其它的費用和為6，②到其它處費用和為11，③到其它處的費用和為9，④到其它處的費用和為6.比較各處到其它各處費用和的大小，可知①和④處到其它各點的費用最小.因此，①和④處就經濟要素而言是最優的.

Dijkstra算法是求最短路徑最常用也是最有效的方法，但是它只能求從某一頂點到其余各頂點的最短路徑.若是用于配送中心的選址問題的情況，對于這種情況，就得重復多次用Dijkstra算法，計算起來比較復雜.而1962年Floyd提出了求任意兩點間最短距離的算法，就能更好的用于這種情況的解決.Dijkstra算法主要是用來標記路徑，而Floyd算法則能在矩陣中直觀的看出結果來.但是，當配送中心候選地較多時Floyd算法也會顯得相當累贅.

4 結語

本文對最短路算法在物流配送中選用的方法進行了分析，同時，最短路算法對物流配送也起到重要的作用，不僅能夠規劃調整物流配送的路線，而且有效地節約物流配送成本.本文將Dijkstra算法與Floyd算法分別應用于物流管理中的配送路徑問題以及配送中心選址問題，并對這兩種算法進行比較.認為Dijkstra算法在物流配送路線規劃方面比較適合，而配送中心選址問題用Floyd算法求解則更簡潔.

〔1〕甘應愛,田豐,李維錚,等.運籌學[M].北京：清華大學出版社，2005.

〔2〕傅彥.離散數學及其應用[M].北京：高等教育出版社，2007.

〔3〕王燕,蔣笑梅.配送中心全程規劃[M]北京:機械工業出版社，2004.

〔4〕刁在筠,等.運籌學(第二版)[M].北京:高等教育出版社，2005.

〔5〕耿娟.工業企業物流網絡規劃[M].西安:西安建筑科技大學，2007.

TP301.6

A

1673-260X（2013）11-0020-03