基于LMS的自適應(yīng)直放站回波消除算法研究

王 鵬 ，王明泉 ,李曉陽(yáng) ，喬佳亮

（中北大學(xué) a.儀器科學(xué)與動(dòng)態(tài)測(cè)試教育部重點(diǎn)實(shí)驗(yàn)室；b.信息與通信工程學(xué)院，山西 太原 030051）

隨著手機(jī)（數(shù)字電視）用戶迅猛增長(zhǎng)，客戶對(duì)覆蓋網(wǎng)絡(luò)優(yōu)化的要求越來(lái)越嚴(yán)格，但由于受到地勢(shì)、功率大小等因素的影響，一些地區(qū)的網(wǎng)絡(luò)信號(hào)難以保持良好，如高樓的陰影區(qū)、地下停車場(chǎng)、邊遠(yuǎn)的郊區(qū)、農(nóng)村等，因此數(shù)字電視的盲區(qū)覆蓋成為下一步網(wǎng)絡(luò)建設(shè)的重點(diǎn)[1]。所以，解決數(shù)字電視地面網(wǎng)絡(luò)信號(hào)覆蓋盲點(diǎn)問(wèn)題就需要使用數(shù)字轉(zhuǎn)發(fā)器。

直放站收發(fā)天線耦合的回波抑制對(duì)于整個(gè)轉(zhuǎn)發(fā)系統(tǒng)來(lái)說(shuō)起著很重要的作用。同頻直放站同時(shí)具有接收天線和發(fā)射天線，而且同頻轉(zhuǎn)發(fā)的情況下，轉(zhuǎn)發(fā)器的輸出為大功率的射頻信號(hào)，與轉(zhuǎn)發(fā)器的輸入是同頻的，而收發(fā)天線間的耦合作用會(huì)使部分轉(zhuǎn)發(fā)的信號(hào)反饋到直放站接收端，在接收天線端產(chǎn)生了經(jīng)過(guò)多徑的回波耦合信道和延遲后的回波信號(hào)，即耦合回波信號(hào)，如果不處理，不僅會(huì)提高接收機(jī)的誤碼率，嚴(yán)重時(shí)還會(huì)導(dǎo)致系統(tǒng)自激[2]。

為了解決上述問(wèn)題，美國(guó)、歐洲、日本對(duì)此做了大量工作，有的采用RLS算法，有的采用NLMS算法，但LMS算法較為簡(jiǎn)單。我國(guó)也非常重視ICS（Interference Cancel System）數(shù)字無(wú)線直放站的研發(fā)。目前較為常用的思路是，利用所采用的算法估計(jì)出回波信道，在數(shù)字基帶進(jìn)行抵消，即可輸出期望的信號(hào)。

1 LMS算法

LMS算法自20世紀(jì)60年代初提出以后得到了廣泛的應(yīng)用。LMS算法最核心的思想是平方誤差代替均方誤差。文獻(xiàn)[3]中作者指出LMS算法的基本關(guān)系式為

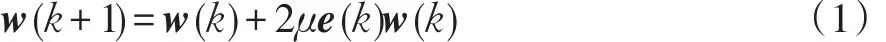
LMS算法進(jìn)行梯度估計(jì)是以誤差信號(hào)每一次迭代的瞬時(shí)平方值來(lái)代替均方值[4-5]，LMS的迭代權(quán)值更新算法式為

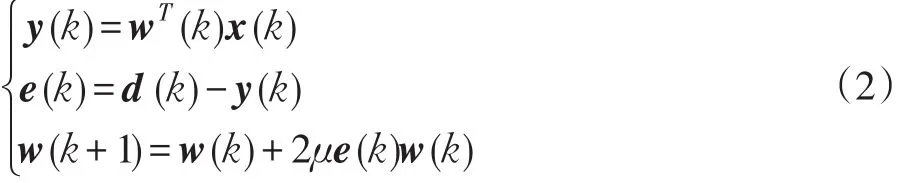
式中：w（k）為濾波器的權(quán)值系數(shù)；μ為自適應(yīng)濾波器的收斂因子，控制自適應(yīng)算法的速度和穩(wěn)定性。為了保證算法收斂，需滿足0〈μ〈λmax，其中λmax為輸入信號(hào)的最大特征值。一般，超量均方誤差Jex等于穩(wěn)態(tài)均方誤差的數(shù)學(xué)期望E[J（n）]與最小均方誤差Jmin之差，即

在穩(wěn)態(tài)情況下

當(dāng)μ較小時(shí)，上式可表示為

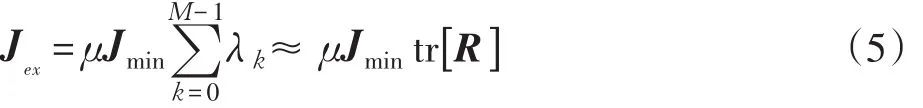
由式（4）和式（5）得到LMS算法的失調(diào)為

自相關(guān)矩陣R的平均特征值為

平均時(shí)間常數(shù)τmse,av定義為

故

所以，可得失調(diào)

由此可得μ越大，自適應(yīng)濾波器的收斂速度越快，但是會(huì)有較大的失調(diào)誤差；相反，μ越小，收斂速度越慢，失調(diào)誤差越小[6-8]。

2 基于LMS算法的回波抵消

同頻直放站對(duì)輸入信號(hào)接收后，經(jīng)過(guò)一些列信號(hào)處理后以相同的頻率將信號(hào)發(fā)射。同頻直放站的難度在于由于發(fā)射鏈路和接收鏈路同頻，所以發(fā)射信號(hào)會(huì)以不同的形式或多或少地耦合到接收鏈路上（通常將這個(gè)信號(hào)叫作回波信號(hào)），這樣，在系統(tǒng)增益不高的情況下，會(huì)影響輸出信號(hào)的質(zhì)量，在系統(tǒng)增益較高的情況，會(huì)引起系統(tǒng)的自激，使系統(tǒng)不能穩(wěn)定工作，甚至燒毀后級(jí)功放。所以在同頻直放站設(shè)計(jì)中如何減小回波對(duì)整個(gè)系統(tǒng)的影響成為設(shè)計(jì)上的最大挑戰(zhàn)。而回波信號(hào)本質(zhì)上是系統(tǒng)的接收信號(hào)放大后，加噪聲和延時(shí)的同頻信號(hào)，針對(duì)回波信號(hào)的以上兩個(gè)特點(diǎn)本文采用了基于LMS算法的自適應(yīng)FIR濾波器，用FIR濾波器的特性模擬發(fā)射天線到接收天線的鏈路特征，通過(guò)FIR濾波器計(jì)算出發(fā)射到接收天線的回波并消除。原理如圖1所示。

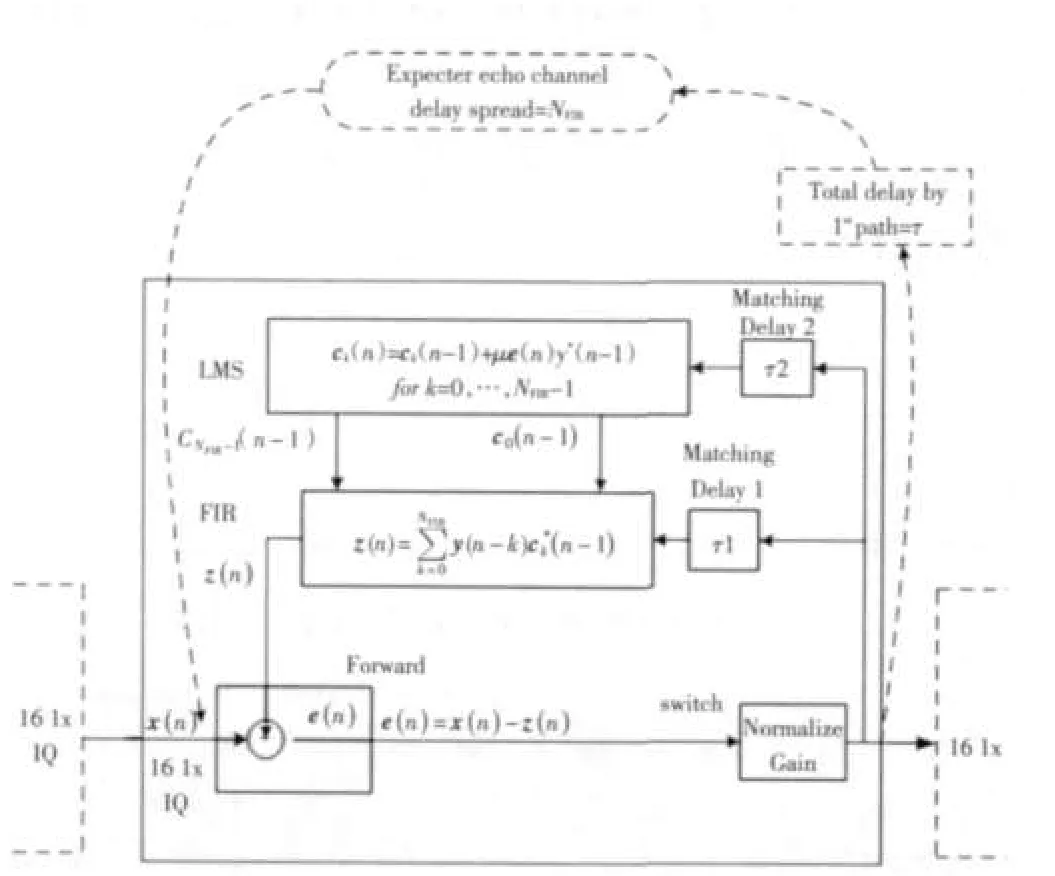
圖1 算法整體框圖

1）用LMS算法計(jì)算出最優(yōu)的的FIR的值。首先，給系數(shù)設(shè)定一個(gè)初值作為參考信號(hào)，然后參考信號(hào)對(duì)輸入信號(hào)開(kāi)始作用，開(kāi)始自適應(yīng)調(diào)整加權(quán)系數(shù)，最終求得一個(gè)合理的e（n）y*（n-k）。原理如圖2所示。

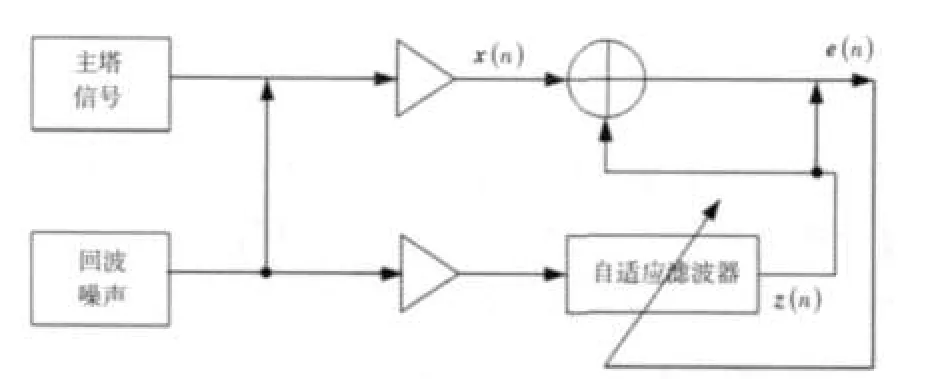
圖2 算法原理圖

式（10）已證明μ越大，自適應(yīng)濾波器的收斂數(shù)度越快，但是會(huì)有較大的失調(diào)誤差；相反，μ越小，收斂速度越慢，失調(diào)誤差越小。

3 仿真及結(jié)果分析

為了驗(yàn)證該算法的有效性和評(píng)估該系統(tǒng)的性能，采用MATLAB中的Simulink進(jìn)行仿真。

實(shí)驗(yàn)一：在設(shè)計(jì)時(shí)還要考慮FIR濾波器的最優(yōu)長(zhǎng)度。理論上更多階數(shù)的FIR濾波器可以消除更加分散的多經(jīng)，但并不是FIR濾波器的長(zhǎng)度越大越好。首先，階數(shù)多時(shí)計(jì)算誤差較大，實(shí)現(xiàn)時(shí)占用的FPGA資源較多。其次，多徑延時(shí)非常長(zhǎng)，也就是說(shuō)這個(gè)回波是從較遠(yuǎn)的地方傳播回來(lái)的，它的傳播路徑較遠(yuǎn)，能量較小，消除它的必要性不足。以上兩點(diǎn)說(shuō)明濾波器的長(zhǎng)度存在一個(gè)最優(yōu)長(zhǎng)度，并非越長(zhǎng)越好。在這里通過(guò)實(shí)驗(yàn)發(fā)現(xiàn)當(dāng)FIR的長(zhǎng)度為170～190時(shí)殘留回波處于一個(gè)最小的范圍，再結(jié)合上面的分析決定選取FIR的長(zhǎng)度為175。對(duì)應(yīng)關(guān)系如圖3所示。

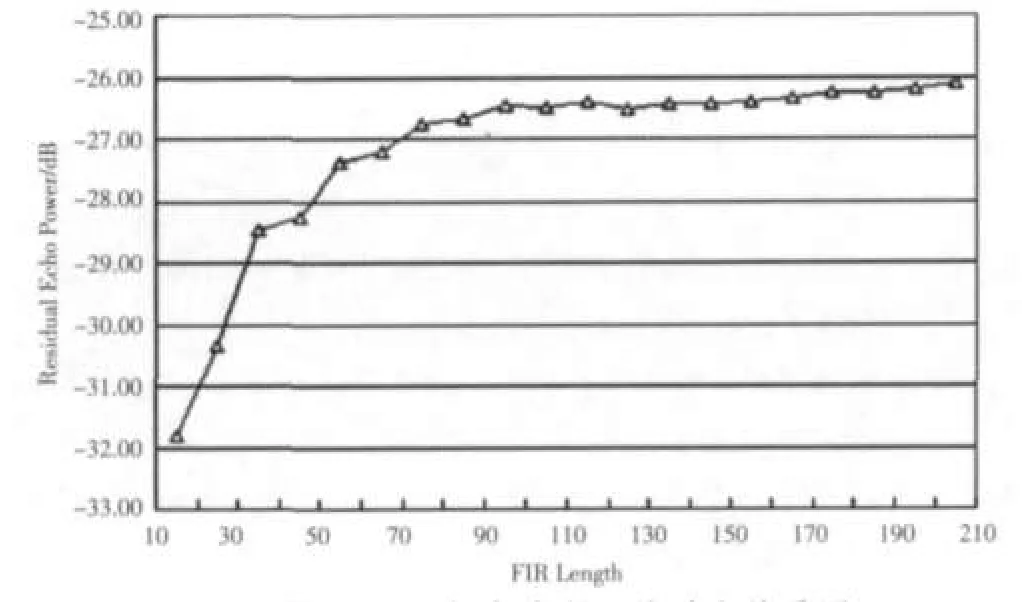
圖3 FIR長(zhǎng)度殘留回波對(duì)應(yīng)關(guān)系圖

經(jīng)過(guò)分析計(jì)算μ的最優(yōu)取值范圍為2-5～2-3，仿真中μ取0.037 7。

實(shí)驗(yàn)表明，開(kāi)啟ICS系統(tǒng)后與開(kāi)啟ICS系統(tǒng)前比較，該系統(tǒng)對(duì)回波有較好的抑制作用。回波抵消仿真模型如圖4所示，結(jié)果如圖5所示。圖5中黃色的波形為回波消除系統(tǒng)開(kāi)啟前的輸出波形圖，藍(lán)色的為回波消除系統(tǒng)開(kāi)啟后的波形圖，實(shí)驗(yàn)結(jié)果表明該系統(tǒng)可有效消除回波。

實(shí)驗(yàn)二：為了進(jìn)一步了解信噪比與回波消除能力的關(guān)系，在FIR長(zhǎng)度一樣的情況下分別給輸入端輸入-30 dB，-20 dB，-10 dB的噪聲與13.70 dB，13.70 dB，14.12 dB的信號(hào)，見(jiàn)表1。得到在信噪比較低的情況下回波消除能力和SNR呈線性關(guān)系，在性噪比較高的情況下為非線性關(guān)系，如圖6所示，圖中case1、case2、case3分別代表輸入噪聲為-10 dB，-20 dB，-30 dB時(shí)的情況。

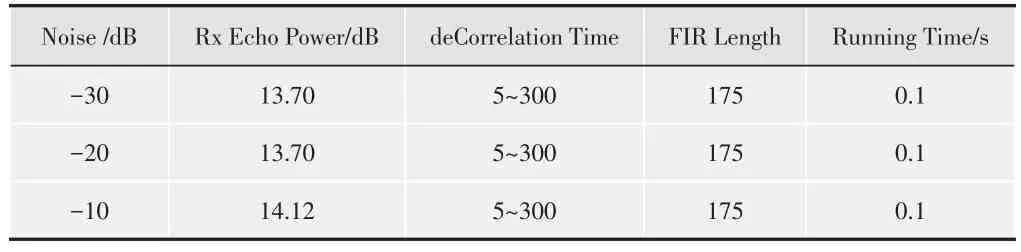
表1 實(shí)驗(yàn)二參數(shù)情況

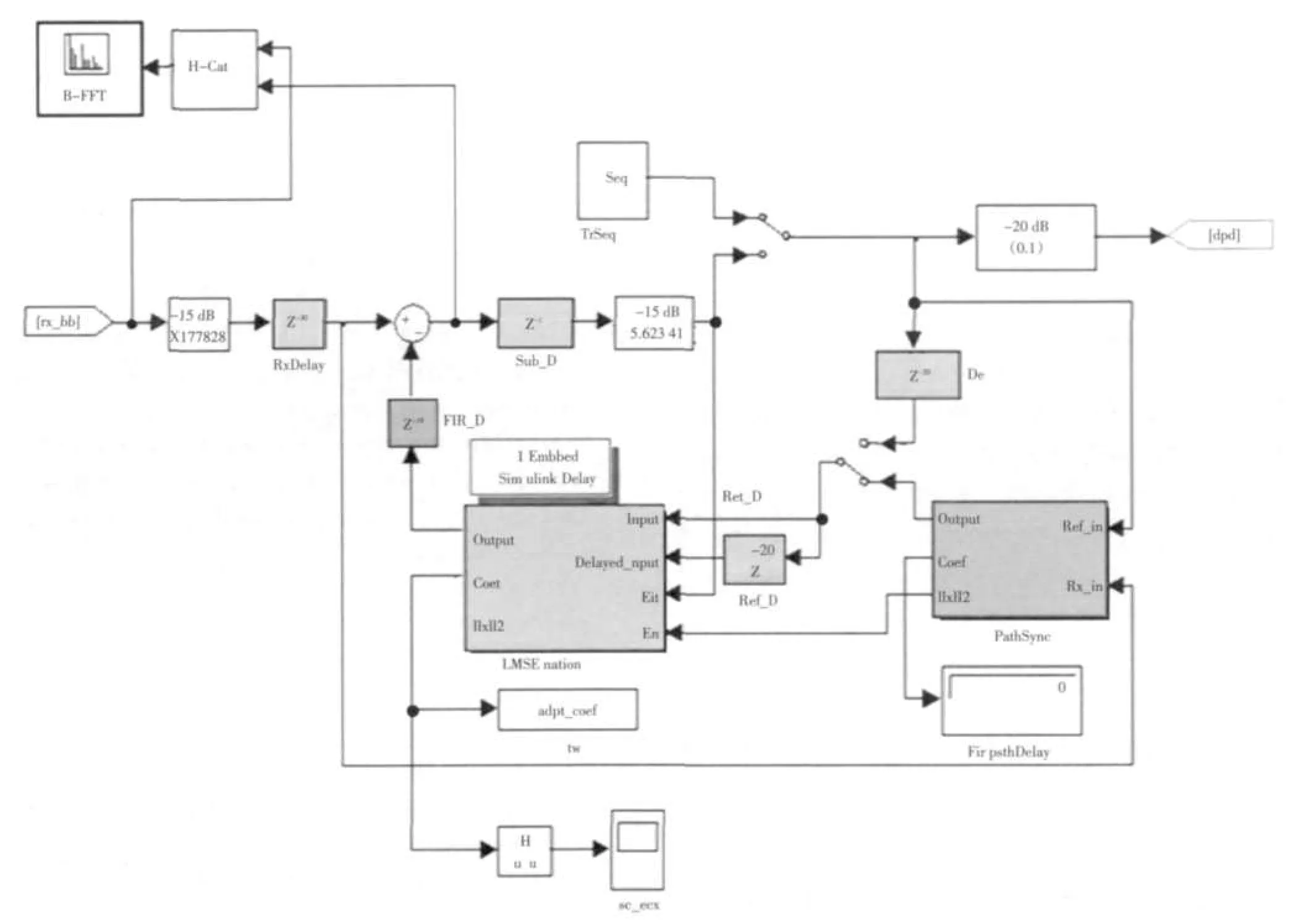
圖4 回波抵消仿真模型

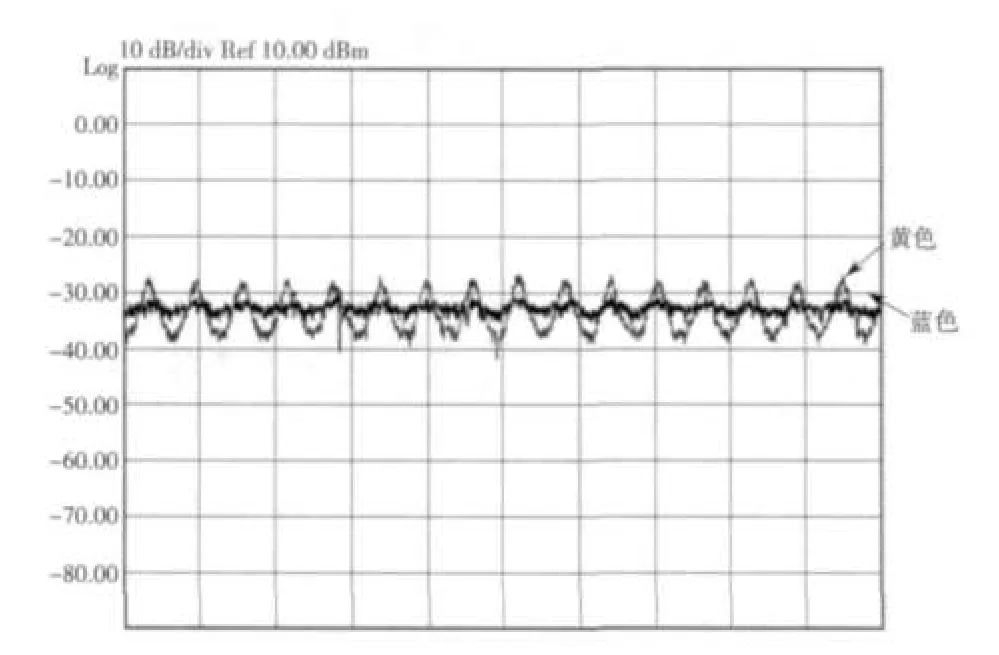
圖5 開(kāi)啟回波消除系統(tǒng)前后輸出波形圖（截圖）

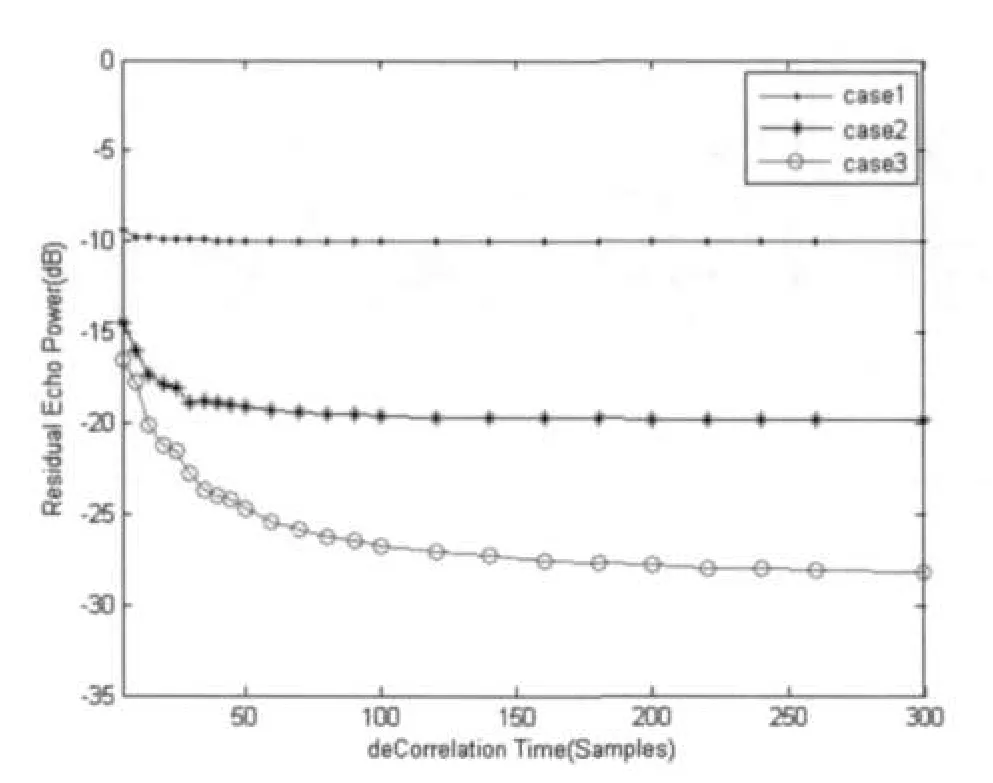
圖6 SNR殘留回波對(duì)應(yīng)關(guān)系圖（截圖）

4 結(jié)論

本文對(duì)基于LMS算法的自適應(yīng)直放站回波抵消算法進(jìn)行了研究，結(jié)果表明該算法可以有效改善信號(hào)的回波對(duì)系統(tǒng)的影響，提高系統(tǒng)的穩(wěn)定性。實(shí)驗(yàn)仿真結(jié)果表明該算法可有效地消除回波，具有良好的使用價(jià)值。

[1] 高鷹，謝勝利.一種變步長(zhǎng)LMS自適應(yīng)濾波算法及分析[J].電子學(xué)報(bào)，2001，29（8）：1094-1097.

[2] 趙春暉，張朝柱.自適應(yīng)信號(hào)處理技術(shù)[M].北京：北京理工大學(xué)出版社，2009.

[3] 姚天任，孫洪.現(xiàn)代數(shù)字信號(hào)處理[M].武漢：華中理工大學(xué)出版社，1999.

[4] 張園，王輝.基于LMS算法自適應(yīng)回波抵消器的Simulink仿真分析[J].現(xiàn)代電子技術(shù)，2008（17）：101-104.

[5] 周建英.基于LMS算法的智能天線波束形成研究及實(shí)現(xiàn)[D].哈爾濱：哈爾濱工程大學(xué)，2008.

[6] 李昕.基于FPGA的自適應(yīng)濾波器設(shè)計(jì)及在回聲消除中的應(yīng)用研究[D].西安：中國(guó)科學(xué)院研究生院，2009.

[7]WIDROW B，MCCOOL J M，LARIMORE M G，et al.Stationary and nonstationary learning eharaeteris ics of the LMS adaptive filter[C]//Proc.IEEE.[S.l.]：IEEE Press，1976：1151-1162.

[8] BUTTERWECH H J.A ware theory of long adapive filters[J].IEEE Trans.Circuits and Systems I:Fundamental Theory and Applications,2001，48（6）：739-747.