基于Z-O編碼的兩層WSNs隱私保護最值查詢處理協議

戴 華 秦小麟 劉 亮 季一木 付 雄 孫 研

①(南京郵電大學計算機學院 南京 210003)

②(南京航空航天大學計算機科學與技術學院 南京 210016)

1 引言

目前，無線傳感器網絡(Wireless Sensor Networks, WSNs)已被廣泛用于諸如環境監測、醫療衛生、智能交通、國防軍事等各種重要領域。而兩層WSNs(Two-tiered Wireless Sensor Networks)[1]是一種以存儲節點(storage nodes)為中間層的無線傳感器網絡，其中存儲節點為計算、存儲和能量資源充足的傳感器節點，其上層為Sink節點，下層為資源受限的一般感知節點(sensor nodes)，存儲節點與查詢區域內其負責管理的所有感知節點構成查詢單元(query cells)。由于兩層WSNs的拓撲結構的簡單性和中間層存儲節點的資源充裕性，使得兩層WSNs具有鏈路質量穩定、路由結構簡單、查詢高效和負載均衡等優點[1,2]。然而，由于存儲節點所處位置的重要性，不僅存儲著大量感知數據，同時還負責執行上層的查詢請求，這就使得存儲節點往往成為各種攻擊的主要目標。研究和解決兩層WSNs中的安全和隱私保護問題，對于促進無線傳感器網絡技術的大規模應用具有重要的現實意義。

在面向兩層 WSNs的隱私保護查詢處理技術中，現有研究重點關注范圍(range)查詢中的隱私保護技術[3-6]，對于最值(MAX/MIN)查詢處理的研究相對較少，目前僅有文獻[7]提出了初步的解決方法，該方法利用前綴編碼驗證(Prefix Membership Verification, PMV)機制[3]，給出了一種無需感知數據明文參與的數值線性關系比較方法，進而實現滿足隱私保護要求的最值查詢處理方法(記為 PMVMQP)。然而，該方法采用的前綴編碼機制產生的數據量較大，并且每一個感知節點都需要加密感知數據并傳送密文數據，導致該查詢處理過程需要較大的能耗開銷。此外，文獻[8]提出了工作于多跳WSN中基于k-隱藏的最值聚集查詢方法，但該方法只能查詢最值數據，無法查詢產生最值數據的傳感器節點位置信息。

本文以兩層WSNs為研究背景，重點討論面向兩層WSNs的隱私保護最值查詢處理技術，即在實現最值查詢處理的過程中，確保感知數據和最值查詢結果不泄露，以保證感知數據和最值查詢結果的隱私安全性。基于此，本文提出了基于Z-O編碼的兩層WSNs隱私保護最值查詢處理協議。通過引入安全多方計算中的Z-O編碼技術[9]，并結合Hash消息身份驗證編碼機制(Hashed Message Authentication Code, HMAC)[10]，對感知數據進行HMAC數值化Z-O編碼處理，然后利用Z-O編碼集合的數值比較特性，實現在無需感知數據明文參與下的數值線性關系比較，并利用加密技術確保感知數據傳輸過程中的隱私安全性。在上述隱私保護措施的基礎上，給出基于Z-O編碼的隱私保護最值查詢處理協議(Z-O Encoding based Privacy Preserving Max/Min query process protocol, ZOPPM)，并對該協議進行能耗和隱私安全性分析。實驗結果表明，ZOPPM協議的能耗優于現有的方法。

2 問題描述

在兩層WSNs的查詢處理過程中，如果不對感知數據進行處理，直接以明文形式參與查詢，當存儲節點被俘獲，該節點將能夠獲取所有存儲在該節點，以及利用該節點進行轉發的感知數據，并且還能夠獲取由該節點計算出的部分查詢結果。與此同時，由于傳感器節點數據通信的廣播特性，在感知節點發送數據的一跳(hop)范圍內，其他任何節點(存儲節點或感知節點)都可以收到數據。因此，需要在查詢處理過程增加隱私保護措施，以確保感知數據和查詢結果的隱私安全性。

最值查詢即為獲取查詢區域內的感知節點采集到的數據最大值(MAX)或最小值(MIN)及其位置信息的計算過程。最值的計算必然需要比較數值的線性關系，所以解決最值查詢問題，首先需要解決如何在不泄露隱私的情況下比較兩個感知節點的數據大小問題，該問題類似于安全多方計算研究中一個經典問題——百萬富翁問題[11]。

與文獻[3,7,8]類似，本文也假設查詢發起節點Sink可信，并假設兩層WSNs中的存儲節點和感知節點都有試圖窺探其他節點數據的企圖，但仍然能夠遵循查詢處理協議進行最值計算，即符合honestbut-curious威脅模型[12]。此外，假設兩層WSNs的拓撲結構穩定，感知節點采集感知數據，存儲節點只負責計算和存儲；存儲節點擁有其負責的感知節點的位置和ID信息，而感知節點也擁有對應存儲節點的位置和ID信息，Sink則擁有所有感知節點和存儲節點的位置和ID信息。

在上述假設條件下，實現具有隱私保護能力的最值查詢，就必須確保查詢處理過程滿足：(1)對于網絡中的任一感知節點的感知數據，只有該感知節點本身和Sink可以讀取其明文數值；(2)對于最終的最值查詢結果(包含數值和位置信息)，只有Sink擁有，而其他任何節點都無法獲得。此外，存儲節點的能量資源充足，而感知節點的能耗有限，因此，降低感知節點的能耗開銷也是兩層WSNs查詢處理技術研究的一個重要目標。

3 基于Z-O編碼的數值比較方法

本節我們將在文獻[9]的基礎上，給出基于 Z-O編碼數值比較方法。

定義1Z-O編碼(Zero-One encoding)：設包含w個二進制位的數值x=b1b2…bw-1bw(bi∈{0,1}且1≤i≤w)，對x進行Z-O編碼，得到的Z編碼集合Z(x)和O編碼集合O(x)為

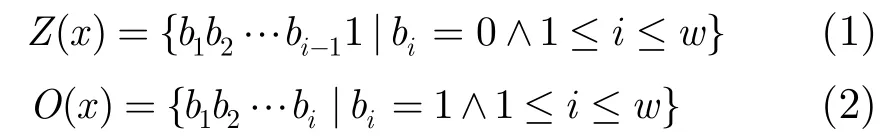
其中b1b2…bw-1bw是數值x的二進制編碼表示，b1為最高位，bw為最低位。

性質1設數值x為包含w個二進制位，則Z(x)和O(x)滿足如下性質：

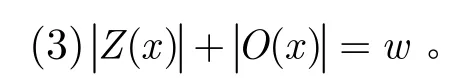
由定義1容易得到性質1成立(證略)。

性質2若已知數值x的Z編碼集合或O編碼集合，不難反向逆推出數值x。

由定義1中的Z-O編碼方法及性質1的內容，易得性質2成立。例如，若已知包含4個二進制位的數值x的Z編碼集合Z(x)={1}，則x必定為0111。

定理1對于都包含w個二進制位的數值x和y，當且僅當O(x)與Z(y)不相交時，x＞y成立；當且僅當O(x)與Z(y)存在非空交集時，x≤y成立，即有式(3)和式(4)成立。

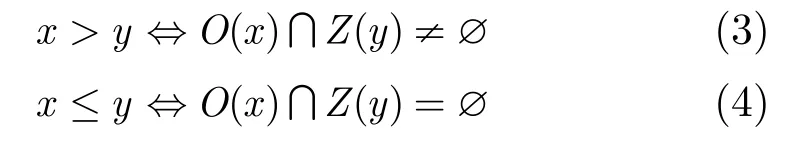
定理1的證明詳見文獻[9]。由定理1可知，數值x和y的大小比較問題，可以轉化為判斷Z編碼集合與O編碼集合是否存在交集的問題。顯然，如果將Z編碼集合和O編碼集合中的元素都轉換為具體數值，則可以簡化集合相交的計算過程。為了保持Z-O編碼的數值比較特性，對于Z-O編碼的數值化方法必須滿足定義2要求。

定義2若將任意Z-O編碼二進制序列p的數值化方法記為N，得到的數值化Z-O編碼記為N(p)，則對于任意兩個Z-O編碼二進制序列p1和p2，該數值化方法應滿足：

(1)p1=p2?N(p1)=N(p2)；

(2)p1≠p2?N(p1)≠N(p2)。

顯然，針對Z-O編碼的數值化方法并不唯一。本文給出一種簡單的數值化方法Ns：對于數值x的任一Z-O編碼序列p=b1b2…bi，則p數值化后得到Ns(p)=1b1b2…bi，即在二進制序列b1b2…bi的最高位之前增加“1”。容易證明，該數值化方法Ns符合定義2要求。

4 基于 Z-O編碼的隱私保護最值查詢處理方法

4.1 基本思想

在介紹本文研究工作的基本思想之前，我們首先給出查詢單元的形式化定義。

定義3查詢單元(query cell)：存儲節點S與其在查詢區域內的負責的所有感知節點?={s1,s2,…,sn}(?≠?)構成一個查詢單元，記為 qcS=(S,?)。

根據定義3的要求，任一查詢單元只包含一個存儲節點，且至少包含一個感知節點。此外，由于存儲節點擁有其負責的感知節點的位置信息，因此，該存儲節點能夠計算出其所在的查詢單元或者不構成查詢單元。為了方便討論，我們假設任一感知節點最多只存在于一個查詢單元中。

本文的面向隱私保護的最值查詢處理方法的基本思想主要包含如下兩個階段：

(1)查詢指令廣播階段首先 Sink將查詢指令MQ={t,qa, MAX/MIN}(表示查詢滿足時刻t和區域qa要求的最大/最小的感知數據)廣播到所有存儲節點；存儲節點S收到MQ后，判斷是否構成查詢單元qcS，若構成，則S再將MQ轉發至qcS內的所有感知節點，否則不參與查詢處理。

(2)最值查詢處理階段在每一個查詢單元 qcS=(S,{s1,s2,…,sn})中，si發送其感知數據的 HMAC數值化Z-O編碼數據給S；根據收到的qcS內所有感知節點發來的編碼數據，S計算出qcS內產生最值的節點sj，并通知sj發送感知數據；當sj收到S的數據請求，sj立即加密其感知數據，并將密文發回給S；而S收到密文數據后，構造qcS的局部查詢結果lqr(local query result)并發送給Sink；最后，Sink根據各個查詢單元發送的lqr，計算出最終的全局查詢結果gqr(global query result)，并返回給用戶。

在查詢處理階段，為了確保感知數據和查詢結果的隱私安全性，我們采取如下隱私保護措施：

(1)當si需要發送其感知數據di給S時，首先利用對稱加密方法(如RC4, RC5, IDEA等)對di進行加密處理，生成密鑰為ki的加密數據(di)ki,si僅與Sink共享ki，然后將(di)ki發送給S；

(2)為了消除Z-O編碼的可逆推性，在編碼過程中增加HMAC處理。HMAC機制的單向性和抗沖突性，將使得感知數據di經過 HMAC數值化處理后，即可得到不可逆的 HMAC數據集合 HMACg(Ns(Z(di)))和HMACg(Ns(O(di)))，其中g為所有感知節點共享的HMAC密鑰。

4.2 具有隱私保護能力的最值查詢處理協議ZOPPM

下面，我們以最大值查詢處理為例，給出兩層WSN中基于Z-O編碼的隱私保護最值查詢處理協議。我們分別從查詢單元和Sink節點這兩個方面，討論ZOPPM協議的工作過程。

設lqrHMAC為存放HMAC數值化Z-O編碼數據的變量，lqrnode為存儲感知節點ID的變量，lqr(S)={id, cv}為存儲節點S所在查詢單元的局部查詢結果變量，gqr={id, pv}為存儲全局查詢結果的變量，其中id為感知節點ID, cv為密文數據，pv為明文數據，MD為密文傳送指令。則具體協議內容如表1所示。

由ZOPPM協議內容可知，兩層WSN中的最值查詢處理由Sink，存儲節點和感知節點共同協作完成。在查詢處理過程中，加密機制確保了感知數據在傳輸過程中的安全性，而HMAC機制的應用，使得惡意節點無法利用Z-O編碼反向逆推原始感知數據，進而保證了兩層 WSN中感知節點的隱私安全性。

表1 基于Z-O編碼的隱私保護最值查詢處理協議

4.3 協議分析

4.3.1隱私安全性分析我們主要從感知數據和查詢結果角度，分析ZOPPM協議的隱私安全性。

(1)感知數據的隱私安全性 在本文基于可信Sink節點的前提下，對于任意感知節點si及其本地感知數據di而言，僅當查詢處理方法能夠確保其它感知節點和存儲節點都無法獲取di時，di才是隱私安全的。而我們提出的ZOPPM協議能夠保證感知數據的隱私安全性：

首先，在最值查詢處理過程中，si在傳輸di時，需首先利用對稱加密方法對di進行加密處理(密鑰僅與 Sink共享)。因此，在無密鑰的情況下獲取di的復雜度與破解加密算法相同，從而確保任意傳輸路徑中的其它感知節點或存儲節點都無法獲取其明文數據。

其次，我們利用HMAC機制，對感知節點發送給存儲節點的數值化Z-O編碼集合進行HMAC處理，使得存儲節點在無需感知數據明文參與的情況下，即可實現各感知數據的大小比較；同時也使得其它能夠獲得HMAC數據的節點，都無法反向逆推其對應的感知數據。

(2)最值查詢結果的隱私安全性 最值查詢結果由最值數據和最值位置這兩方面組成。其中，最值數據同樣也是由某個感知節點產生的感知數據，由本節(1)中的討論可知，最值數據的隱私安全性同樣能夠保證。這里，我們重點分析ZOPPM協議對于最值位置的隱私保護能力。

對于最值查詢處理而言，產生最值的感知節點的位置信息同樣也需要保護。假設網絡中共有k個構成查詢單元的存儲節點，則這些存儲節點將產生k個局部查詢結果(包含局部最值的位置信息)，而最終的全局查詢結果在其中產生，并由Sink負責計算。可見，全局查詢結果的位置信息，隱藏在k個局部查詢結果中，任一存儲節點獲得全局查詢結果位置的概率僅為1/k。因此，ZOPPM協議對最值位置的隱私保護滿足k-隱藏(k-indistinguishable)特性，其中k為網絡中構成查詢單元的存儲節點的數量。

由上述隱私安全性分析可知，ZOPPM 協議具有較好的隱私安全保護能力，不僅能夠確保感知數據的隱私安全，同樣能夠保護最值查詢結果的隱私安全性。

4.3.2能耗分析在兩層WSN中，由于存儲節點具有充足的存儲空間和能量儲備，因此，整個網絡的生命周期主要受感知節點的能耗影響。為了盡可能提高網絡的生命周期，我們以降低感知節點的能耗為主要目標。

在本文的最值查詢處理方法中，感知節點的總能耗Etotal的計算公式如式⑸所示，

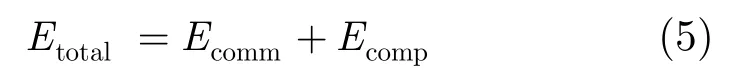
其中Ecomm表示感知節點接收和發送數據所帶來的通信能耗，Ecomp表示感知節點進行加密和 HMAC計算所帶來的計算能耗。

由ZOPPM協議可知：每個感知節點收到存儲節點發送的MQ和MD各一次；并且，每個包含w位的感知數據對應的 Z-O編碼集合將包含w個HMAC數據；此外，每個查詢單元中將有一個感知節點對本地感知數據進行加密，并發送密文數據給存儲節點。因此，通信能耗Ecomm為

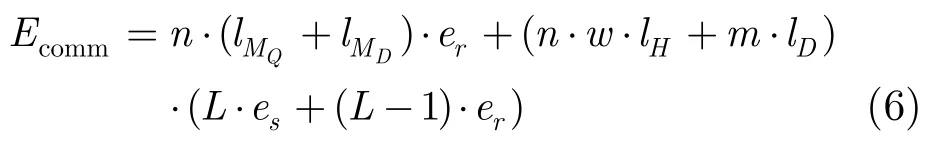
此外，計算能耗Ecomp為感知節點進行加密和HMAC計算的能耗之和，則有

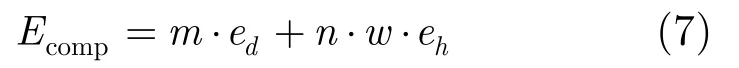
由式(6)，式(7)進而可以得到感知節點的總能耗Etotal的最終計算公式為

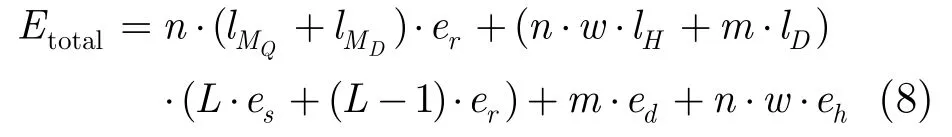
而文獻[7]提出的基于前綴成員驗證的兩層WSN最值查詢處理方法(PMV-MQP)，其基本思想為：對于任一感知節點si的感知數據di∈[dbot,dtop](dbot和dtop分別為感知數據的已知下界和上界)，si針對di和[di,dtop]分別計算相應的HMAC數值化前綴編碼集合F和S，若di包含w個二進制位，則F和S滿足|F|=w+1和 1≤|S|≤2w-2,si需要計算的HMAC數據總量為|F|+|S|∈[w+2, 3w-1]；同時，si還對di進行加密處理，然后將 HMAC數據和加密數據都發送給存儲節點，以進行后續的最值查詢處理。可見，PMV-MQP總能耗在理論上存在上限和下限；并且，與本文提出的ZOPPM相比，在同等情況下PMV-MQP將消耗更多的通信和計算能耗。我們將在第5節對ZOPPM和PMV-MQP的能耗問題作進一步的實驗對比分析。

5 實驗分析

為了對協議的性能進行比較和分析，本文在文獻[13]的仿真器上實現了ZOPPM與PMV-MQP。通過模擬仿真，我們對這兩種方法的能耗進行對比試驗，其中，PMV-MQP(top)和 PMV-MQP(bot)分別表示PMV-MQP的能耗上限和下限；同時，我們還對ZOPPM的通信和計算能耗進行對比實驗，以評測通信和計算能耗對總能耗的影響情況。本文的實驗環境為Pentium E5700(雙核3.0 GHz)CPU,3 G內存；軟件環境為 Windows XP操作系統，Eclipse和 Matlab；實驗數據集為 Intel Lab Data[14]。

本文采用與文獻[15]相同的能耗計算方法：無線通信電路發送和接收1 byte的能量消耗公式為es=α+γ×dk和er=β，其中，α為通信發送電路消耗的能量，γ為傳輸放大器消耗的能量，d為傳輸距離，k為路徑損失因子，β為通信接收電路消耗的能量。我們采用文獻[13]的參數：γ=10 pJ/bit/m2,α=45 nJ/bit,β=135 nJ/bit,k=2。此外，感知數據長度初始設置為10 bit，加密計算的初始能耗采用文獻[8]給出的TelosB中利用RC4對10 bit數據進行加密的能耗數據8.92 μJ，并假設HMAC計算的能耗與加密計算相同。其它參數設置如表2所示。

表2 實驗參數

在每一組實驗中，我們通過在網絡覆蓋區域中隨機分布感知節點，生成20組不同拓撲結構的網絡(用不同的網絡ID標識)，進而通過計算20組網絡的平均能耗值確定最值查詢的總能耗。具體實驗結果及分析如下：

(1)在實驗設置的初始參數條件下，隨機生成的20組網絡的能耗實驗結果如圖1所示。

由圖1(a)可知，在不同拓撲的網絡中，ZOPPM和PMV-MQP的能耗均變化不大，且分布都較為均勻，但ZOPPM的能耗始終低于PMV-MQP。并且，與其能耗下限相比，ZOPPM平均節省約23.03%的能耗開銷。由圖1(b)可知，在ZOPPM的總能耗中，計算能耗Ecomp和通信能耗Ecomm的變化都不大，但通信能耗占總能耗的絕大部分(約99.96%)。可見，在隨機生成的不同拓撲結構的網絡中，ZOPPM和PMV-MQP的能耗均變化不大，但ZOPPM的能耗表現明顯較優，其能量消耗絕大部分由數據通信產生。

(2)以感知節點數量n為自變量，其它參數保持初始設置不變，得到如圖2所示的實驗結果。

由圖2(a)可知，隨著感知節點數量n的增長，感知節點發送的數據消息也增多，導致ZOPPM和PMV-MQP的總能耗都顯著增長，其中PMV-MQP的增長幅度較大，這是由于前者的任一查詢單元中，僅有一個感知節點需要發送密文數據，而后者所有的感知節點卻都需要發送。在本組實驗設置下，ZOPPM的總能耗始終少于PMV-MQP，與后者的能耗下限相比，ZOPPM平均節省約23.05%的能耗開銷。由圖2(b)可知，在ZOPPM的能量消耗中，隨著n的增長，Ecomm有顯著增長，雖然Ecomp也同步增長，但由于其占總能耗的比重非常小(平均約占0.02%)，其增長趨勢不明顯。

(3)以w為自變量，其它參數保持初始設置不變，得到如圖3所示的實驗結果。

由圖3(a)可知，隨著感知數據長度w的增大，ZOPPM和PMV-MQP的總能耗也隨之增大，這是由于查詢單元中的所有感知節點都需要傳送HMAC數據，而w的長度與感知節點傳送HMAC數據的數量成正比，因此，兩者的總能耗都同步增長，但ZOPPM的總能耗始終少于PMV-MQP，與后者的能耗下限相比，ZOPPM平均節省約17.1%的能耗開銷。由圖3(b)可知，在ZOPPM消耗的總能量中，通信能耗占總能耗的絕大部分(平均約99.96%)，計算能耗所占比重則非常小。

綜合上述實驗結果及分析可知：本文的ZOPPM的能耗優于文獻[7]提出的PMV-MQP，在本文的實驗設置條件下，ZOPPM比PMV-MQP的能耗下限平均節省近 20%的能量消耗；并且，在ZOPPM 協議中，收發數據的通信能耗占總能耗的絕大部分，而計算能耗所占的比重較小。

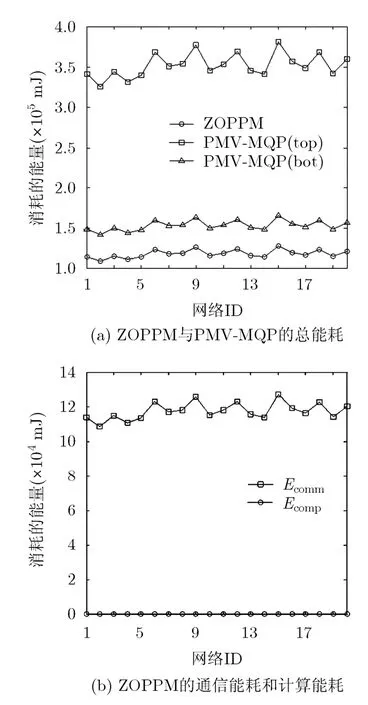
圖1 不同網絡拓撲下的能耗實驗結果

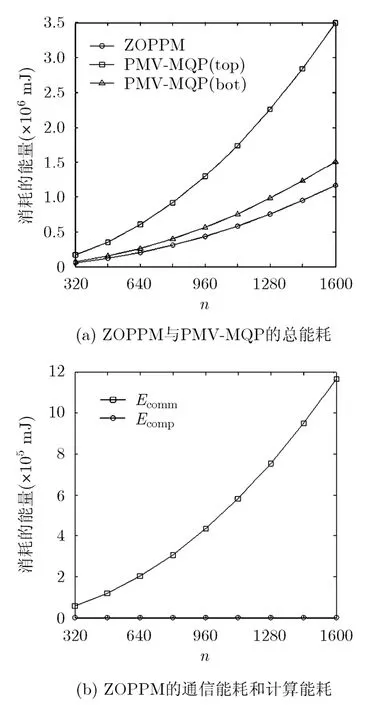
圖2 以n為自變量時的能耗實驗結果

圖3 以w為自變量時的能耗實驗結果

6 總結

數據隱私保護問題是無線傳感器網絡中具有共性要求的問題，在諸如環境監測、醫療衛生、智能交通、國防軍事等各種重要領域都有著迫切的需求，是無線傳感器網絡研究中的一個熱點問題。然而，現有的兩層WSNs重點關注范圍等查詢處理方法，對最值查詢處理方法的研究相對較少。本文提出了一種基于Z-O編碼的兩層WSNs隱私保護最值查詢處理協議。在該協議中，感知節點利用Z-O編碼機制，并結合Hash消息身份驗證編碼方法，對本地感知數據進行HMAC數值化Z-O編碼處理，并發送至存儲節點；而存儲節點則利用Z-O編碼的數值比較特性，實現在無需感知數據明文參與下的數值線性關系比較，進而獲得所在查詢單元中產生局部最值的感知節點，并通知該感知節點計算并傳送加密數據，然后構造局部查詢結果并發送給Sink；最終由Sink完成最值查詢結果的計算，并返回給用戶。理論分析和實驗結果表明，ZOPPM 協議能夠確保感知數據和最值查詢結果的隱私安全性，并且其能耗優于現有的方法。

[1]Gnawali O, Jang K Y, Paek J,et al.. The tenet architecture for tiered sensor networks[C]. Proceedings of the 4th ACM Conference on Embedded Networked Sensor Systems,Boulder, Colorado, USA, 2006: 153-166.

[2]Yang D, Misra S, Fang X,et al.. Two-tiered constrained relay node placement in wireless sensor networks: computational complexity and efficient approximations[J].IEEE Transactions on Mobile Computing, 2012, 11(8): 1399-1411.

[3]Chen F and Liu A X. SafeQ: secure and efficient query processing in sensor networks[C]. 29th IEEE International Conference on Computer Communications, San Diego, CA,USA, 2010: 1-9.

[4]Sheng B and Li Q. Verifiable privacy-preserving range query in two-tiered sensor networks[C]. 27th IEEE International Conference on Computer Communications, Phoenix, AZ,USA, 2008: 46-50.

[5]Shi J, Zhang R, and Zhang Y. Secure range queries in tiered sensor networks[C]. 28th IEEE International Conference on Computer Communications, Rio de Janeiro, Brazil, 2009:945-953.

[6]Shi J, Zhang R, and Zhang Y. A spatiotemporal approach for secure range queries in tiered sensor networks[J].IEEE Transactions on Wireless Communications, 2011, 10(1):264-273.

[7]Yao Y, Xiong N, Park J H,et al.. Privacy-preserving max/min query in two-tiered wireless sensor networks[OL].Computers & Mathematics with Applications. http://www.sciencedirect.com/science/article/pii/S08981221120011 74. 2012, 2.

[8]Groat M M, Hey W, and Forrest S. KIPDA:kindistinguishable privacy-preserving data aggregation in wireless sensor networks[C]. 30th IEEE International Conference on Computer Communications, Shanghai, China,2011: 2024-2032.

[9]Lin H Y and Tzeng W G. An efficient solution to the millionaires’ problem based on homomorphic encryption[C].Proceedings of the 3rd International Conference on Applied Cryptography and Network Security, New York, NY, USA,2005: 97-134.

[10]Krawczyk H, Canetti R, and Bellare M. HMAC:keyed-hashing for message authentication[R]. RFC 2104,1997.

[11]Yao A C. Protocols for secure computations[C]. 23rd Annual Symposium on Foundations of Computer Science, Chicago,Illinois, USA, 1982: 160-164.

[12]Bozovic V, Socek D, Steinwandt R,et al.. Multi-authority attribute-based encryption with honest-but-curious central authority[J].International Journal of Computer Mathematics,2012, 89(3): 268-283.

[13]Coman A, Sander J, and Nascimento M A. Adaptive processing of historical spatial range queries in peer-to-peer sensor networks[J].Distributed and Parallel Databases, 2007,22(2): 133-163.

[14]Samuel M. Intel lab data[OL]. http://db.csail.mit.edu/labdata/labdata.html. 2004.6.

[15]Coman A, Nascimento A M, and Sander J. A framework for spatio-temporal query processing over wireless sensor networks[C]. Proceeedings of the 1st International Workshop on Data Management for Sensor Networks, Toronto, Canada,2004: 104-110.