振蕩積分的數值計算與Matlab實現

陳衛紅

（安徽財貿職業學院，安徽 合肥230601）

振蕩積分的數值計算與Matlab實現

陳衛紅

（安徽財貿職業學院，安徽 合肥230601）

本文提出利用樣條函數計算及類型的振蕩積分，在每個比較小的子區間采用分部積分法，避免了整體利用分部積分需要計算函數在區間端點處的高階導數，能提高計算的精確度.

振蕩積分；樣條插值；Matlab實現

1 背景導引

2 積分計算原理分析

設f(x)的樣條插值函數為S(x)，則

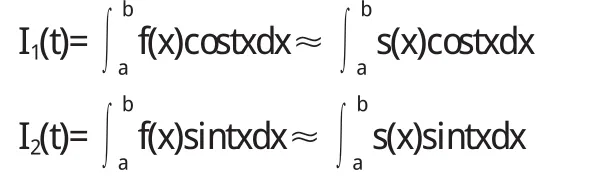
首先，將積分區間[a,b]n等分，h=(b-a)/n，結點坐標為xi=a+ih(i=0,1,…,n)

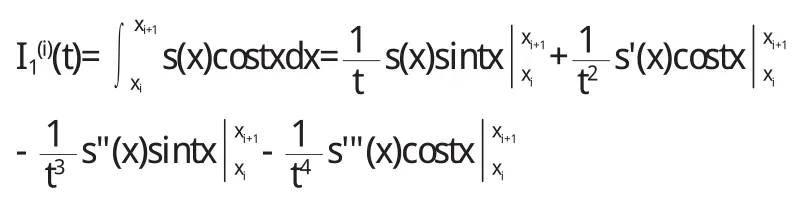
由于在每一個區間上的s(x)為三次多項式，因此s'"(x)為一常數，且在子區間[xi,xi+1]上

令s"(xi)=Ti則有s'(x0)=s'(a)=f'(a)，s'(xn)=s'(b)=f'(b)

于是有

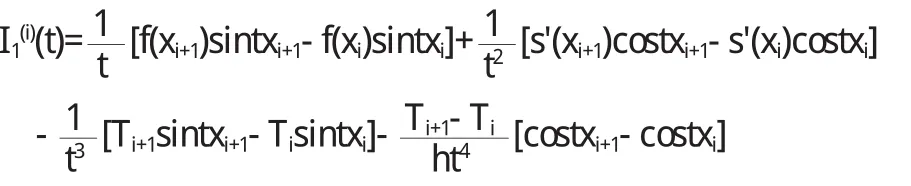
利用類似方法得到

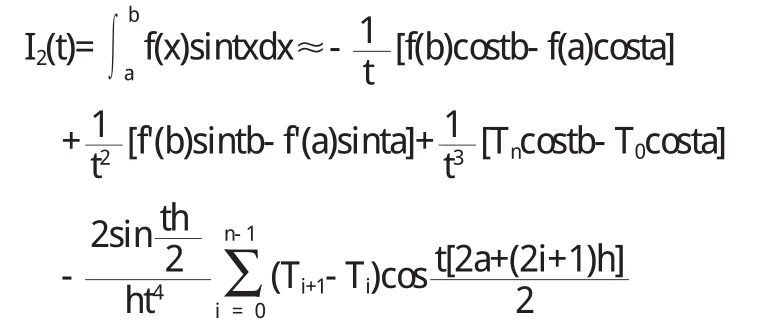
如果積分區間為[0,2π]，則上述兩個公式就變為

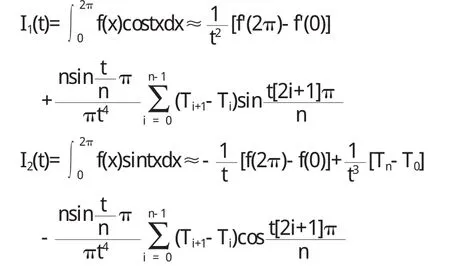
如果等分數n能除盡t，則上述兩個公式又可化簡為

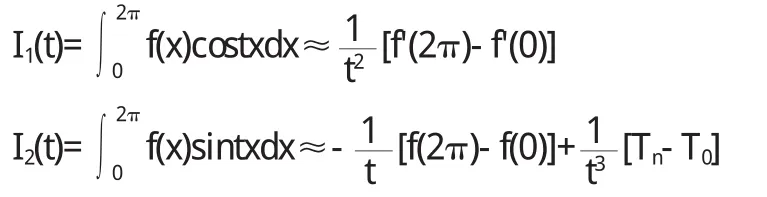
3 Matlab實現

利用Matlab自編T文件或它自帶的樣條插值計算工具箱算得T0=-1.73908T3=-6.80476

一般來說，用樣條函數來處理振蕩積分能大大提高精確度．

〔1〕孫志忠.數值分析[M]．南京：東南大學出版社，2002．

〔2〕張德榮.計算方法與算法語言[M]．北京：高等教育出版社，1981.

O246

A

1673-260X（2013）12-0004-01