基于主成分分析和RBF神經網絡的公路貨運量預測模型

蔣林利

數據挖掘是一種從數據庫中發現知識的過程，它可對知識進行自動提取和分析，因而它與信息系統、數據庫技術之間都存在密切的聯系。數據挖掘的對象并不局限于某一個數據庫，不論是一般數據庫、高級數據庫、關系型數據庫還是信息系統，只要是需要進行數據挖掘的系統都可以成為數據挖掘的研究對象。數據挖掘的內容就是從數據庫大量的數據中挖掘出有用的信息，為行業提供制定決策所需的依據。根據挖掘任務不同，數據挖掘可分為兩種，一種是描述一種是預測，描述任務相對預測任務而言更為簡單，它只需提取數據的表面性質，而預測任務則需對提取的數據進分析和預測。本文以國家統計局編印的《中國統計年鑒》為研究背景，對運輸行業和郵電行業的公路貨運量進行分析，并在此基礎上運用數據挖掘技術中的RBF神經網絡算法，構建公路貨運量預測模型。

一、主成分分析法

主成分分析法是一種將多個變量通過線性變化以選出較少個數重要變量的多元統計法，這種統計法可有效地針對變量間復雜的關系進行簡化處理，從而達到降低信息損失量，形成線性組合的目的。主成分分析方法是建立在降維思想的基礎上，由于它對每個變量都進行了不同程度和不同角度的考慮，所以它統計出來的信息實用度都較高，且各指標間都存在重疊和交叉，所以指標的個數也從多個發展成綜合指標，綜合指標的形成不僅保證信息的精確、全面，還能提高信息的抓取速度。主成分分析法的運用簡化了研究人員的工作分析量，在將研究重點放在主要成分信息的同時抓住了主要信息的重點內容，掌握事物內部變量規律的過程更為簡單，研究人員的工作效率得到了有效的提升。

二、RBF神經網絡算法

由于RBF神經網絡在逼近任意連續函數時精度不受限制，所以它又屬于局部逼近網絡。當樣本數據的個數為n，屬性為m，在神經網絡徑向基函數中的輸入向量應為 X=（X1，X2，…，Xm），函數的輸出向量應為Y=（Y1，Y2，…，Ys）。在上述向量中，s代表輸出節點維數，m代表輸入節點維數。隱含層包含的高斯函數具有一定的輻射狀作用，如下所示為高斯函數：

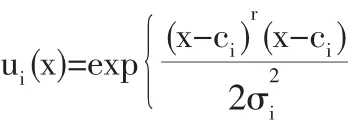
在上述公式中，ui(x)表示隱節點i的輸出；樣本輸入向量用x表示；ci表示隱節點i的中心向量，它和樣本輸入向量x的維數相同；σi是一個標準常數。

高斯函數的數學表達式非常簡單，即使輸入的量為多變量也不會使運算復雜化，兩者之間呈現徑向對稱且光滑型較好，任何數的階導數都存在。隱含層的節點輸出ui(x)表示輸入模式與隱含層節點間呈現分離狀態時，該隱含層節點表示的徑向基函數，在傳統的輸入方法中，隱含層節點的中心向量通常用訓練樣本中隱節點i的輸入向量，因而馴良樣本的個數就表示為隱含層節點的個數。受高斯函數性質的影響，當ui(x)在隱含層節點的中心向量處存在最大值時，ui(x)會隨著(x-ci)的增大而逐漸減小直至取值為零，在衰減過程中只有很少的中心向量靠近x，這部分中心向量才能被激活，若用聚類中心代替部分中心，與聚類中心鄰近的中心向量都可以被激活。隱層節點與輸出層間呈現線性關系，由此可見神經網絡隱含層中的高斯函數為線性函數。

三、RBF神經網絡預測模型在公路貨運量中的預算

（一）經濟數據及公路貨運量

本文用于數據挖掘的數據來源于國家統計局編印的《中國統計年鑒》中的貨運量信息，信息內容有公路總長、公路運量、民用車輛以及私用車輛等。為了驗證數據挖掘技術的精確性，本文選取了2000年至2011年間的所有公路貨運量數據，用于預測2012年的公路貨運量。選取的數據根據年份劃分成11個樣本，將2000年至2009年的公路貨運量數據作為訓練樣本，將2010年的公路貨運量數據作為測試樣本，2011年的公路貨運量數據作為對比樣本。由于數據的屬性和數量級各不相同，所以在處理數據的過程中比較麻煩，為了滿足神經網絡預測算法的要求，在進行數據挖掘前我們首先要對待挖掘的數據進行歸一化處理。然后利用神經網絡算法對預處理后的數據進行預測，輸入結構為X1、X2、X3，輸出量為Y，其中X1表示公路總長度，X2表示民用車輛的輛數，X3表示私人車輛的輛數。將2009年的樣本數據集合成訓練集，將2010年的樣本數據集合成測試集，以此為基礎建立新的神經網絡預測模型，對訓練集和測試集中的數據進行預測。

（二）公路貨運量數據預處理

時域因素和關聯因素都會影響到公路貨運量的預測信息，公路貨運量數據經過預處理后便可形成對應的綜合延拓矩陣。關聯預測主要是通過對本年的其他因素進行分析從而達到預測公路貨運量的目的，時域預測則是以近幾年的公路貨運量為依據，對今后的發展趨勢作出的一個公路貨運量預測信息。無論是時域因素還是關聯因素，它們與公路貨運量都存在著直接或間接的聯系，為了順利完成數據預處理，提高公路貨運量的預測準確性，本文采用了關聯因素與時域因素相結合的綜合延拓矩陣。首先對數據進行歸一化處理全部統一至[0，1]區間，歸一化處理數據的步驟是找出屬性相同的樣本數據中的最大值，對該屬性進行處理后將每個樣本所有相同的屬性都除以最大值，這樣就能弱化數量級對數據預處理的影響。歸一化處理后的數據就可用線性回歸法和主成分分析法進行數據分析，得出關聯因素（X1、X2、X3）的主成分數據分析結果，再將本年前的四年公路貨運量數據設定為時域因素，同樣用線性回歸法和主成分分析法對數據進行分析，然后得出時域因素（Y1、Y2、Y3）的主成分數據分析結果。

（三）公路貨運量數據預測模型

根據年份將2000年至2009年的公路貨運量數據劃分成9個樣本，然后對這9個樣本數據進行均值聚類，K代表聚類的個數。RBF神經網絡有一個隱含層，而隱含層的中心則是聚類中心，所以隱含層中包含的神經元個數就等于聚類個數，將神經網絡和聚類綜合起來進行反復實驗，然后利用動態聚類算法將聚類K設定為5，獲得如下表所示的下近似集樣本號和上近似集樣本號。表1所示為基于粗糙集的動態聚類結果：

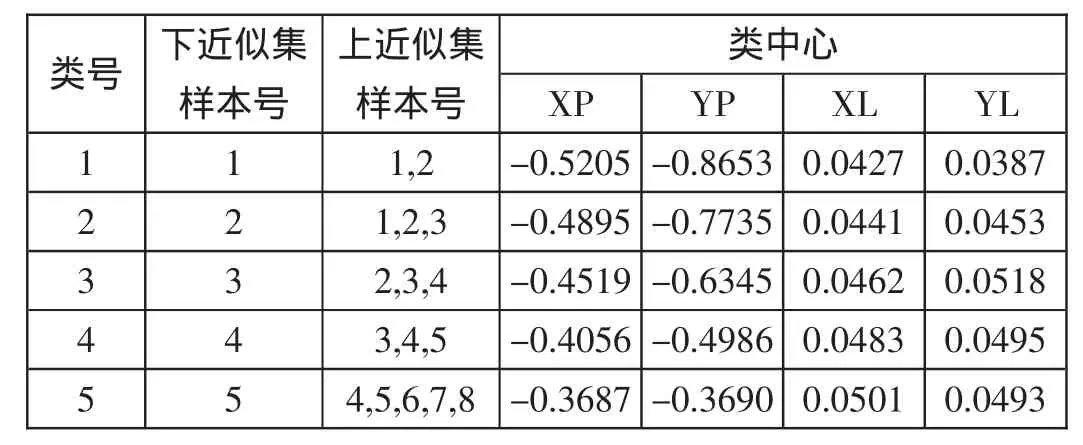
表1 基于粗糙集的動態聚類結果

RBF神經網絡在輸入結構處有三個節點，而隱含層則包含了5個節點，如上文所述將聚類中心作為隱含層的中心，則輸出節點的個數為1個。基于RBF構建的預測模型可以吸收9個樣本中包含的數據信息，而數據信息的體現則是借助綜合延拓矩陣完成的，樣本信息中包含了與公路貨運量相關的屬性分析和一些預測值，神經網絡的構建是以聚類中心為構建中心，在此基礎上學習9個樣本中的數據信息，從而使神經網絡達到一個穩定狀態。

構建穩定的神經網絡，首先需建立神經網絡預測模型，然后選取訓練樣本，訓練樣本數據一般就是這11個數據樣本，利用神經網絡進行預測，預測結果出現的誤差則用均方誤差表示。均方誤差是表示誤差函數常用的方法，通常用MSE來表示，其中T代表實際值而Y則用來表示預測值，具體計算公式如下所示：

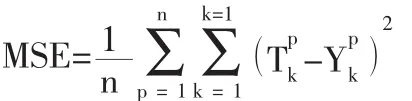
將2011年的數據信息輸入上述公式，得出2011年一年內的公路貨運量，將得出的公路貨運量數據與均方誤差進行比較，得出兩者的誤差。

表2 多種模型的預測性能比較

（四）多種模型的預測性能比較

公路貨運量預測常用方法包括組合預測法、直接預測法和KM-RBF綜合預測法，直接預測法則通過分析公路貨運量歷史數據達到預測的目的，它是借助RBF神經網絡對原始數據進行直接預測；組合預測法主要是用兩種以上的不同預測方法對公路貨運量數據進行預測的一種方法，它與直接預測存在一定的區別，首先要對數據進行預處理，轉變成延拓矩陣才能得出預測結果；KMRBF綜合預測法比直接預測法和組合預測法的精度都要高，相對于簡單的RBF神經網絡算法，KM-RBF綜合預測法在分析能力上有所提升，而輸入結構也得到了簡化，預測顯示的實際值是指該年公路的實際貨運數值。

[1]王純子，張斌.基于隱層優化的RBF神經網絡預測模型[J].計算機工程，2010，36（18）

[2]李曦，王青，萬云輝，李琦.基于RBF神經網絡預測模型及其應用研究[J].泰山學院學報，2008，30（3）

[3]許霞.基于RBF神經網絡的貨運量預測模型[J].航空計算技術，2007，37（5）：28-31