二元域上三次和四次剩余碼的冪等生成元
1.大連大學 信息工程學院,遼寧 大連 116622
2.赤峰學院 附屬中學,內蒙古 赤峰 024000
3.遼寧師范大學 數學學院,遼寧 大連 116029
1.大連大學 信息工程學院,遼寧 大連 116622
2.赤峰學院 附屬中學,內蒙古 赤峰 024000
3.遼寧師范大學 數學學院,遼寧 大連 116029
1 引言
在通信系統中,為提高信息傳輸可靠性,廣泛使用了具有一定糾錯能力的信道編碼技術,如奇偶校驗碼、漢明碼、循環碼等編碼技術。二次剩余碼是特殊的循環碼,又是漢明碼和格雷碼的推廣。因此研究二次剩余碼以及它們的推廣形式具有重要的理論意義和實際價值。文獻[1]的第十六章討論了二元域F2上四種二次剩余碼之間的關系,給出了四種二次剩余碼的冪等生成元。文獻[2]用冪等生成元定義了有限環Z4上的二次剩余碼。文獻[3]證明了在有限環Z2k上由冪等元定義的二次剩余碼存在,且只有4個。另一方面,文獻[4-7]定義了有限域Fq上的高次剩余碼,給出了這些碼生成多項式的形式。高次剩余碼的生成多項式都是多項式xn-1的因式。然而要求出這些高次剩余碼,就需要在有限域Fq上分解 xn-1。當n很大時,這是一件十分困難的任務。如果能夠確定高次剩余碼冪等生成元,求這些冪等生成元與xn-1最大公因式就可得到高次剩余碼生成多項式而不用分解xn-1[1]。本文給出了二元域F2上三次和四次剩余碼的冪等生成元表達式。
2 預備知識
定義1[5]如果方程xt≡2(modp)有解,則稱2是模 p的一個t次剩余。


定義3[1]設p是奇素數,若e(x)∈F2[x]/(xp-1)滿足 e(x)2≡e(x)(mod(xp-1))則稱e(x)為F2[x]/(xp-1)的冪等元。能生成循環碼的冪等元e(x)稱為冪等生成元。
定義4[8]設C是有限域Fq上長為n的循環碼,又設α是 Fq的擴域上n次本原單位根,Z={αi|i∈T}是C的根集合,則稱T是C的定義集。

定義5[8]設 a是整數并且 (a,n)=1,定義映射 iμa≡ia(modn),i∈{0,1,…,n-1},將此定義延伸到 Fq[x]/(xn-1)使得 f(x)μa≡ f(xa)(modxn-1),f(x)∈ Fq[x]/(xn-1)。
引理4[8]設C是有限域Fq上長為n并且以T為定義集的循環碼,a是整數并且(a,n)=1,a-1是a模n的乘法逆,則a-1T(modn)是循環碼Cμa的定義集。
引理5[8]設e(x)是循環碼C的冪等生成元,則e(x)μa是循環碼Cμa的冪等生成元。
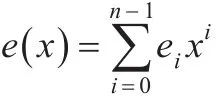
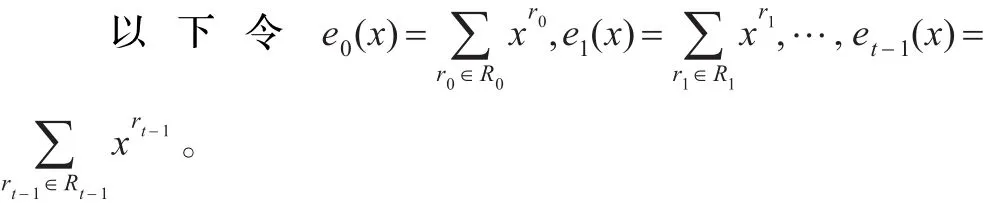
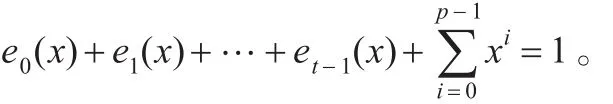
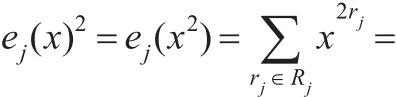

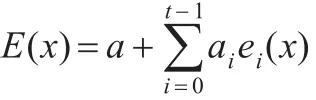
證明設E(x)是t次剩余碼C的冪等生成元,則C的定義集為某個Rl或={0}∪Rl。由于每個Ri都是分圓陪集之并,故可設Ri=Ci1∪Ci2∪…∪Civi,其中Cik都是分圓陪集,i∈{0,1,…,t-1}。由 R0∪R1∪…∪Rt-1={1,2,…,n-1}和引理6可設:
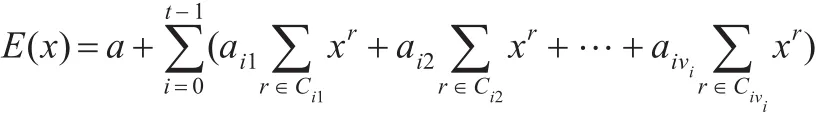
因為 Ri={ρtk+i∈FP|k∈Z},其中 i∈{0,1,…,t-1},故不妨設 Ci1={ρi,2ρi,…} 。如果 Cif={ρtf+i,2ρtf+i,…} ,則取d=ρtf∈R0。于是 dCi1=Cif從而
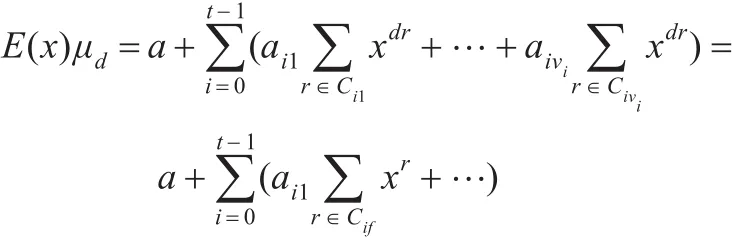
又因為
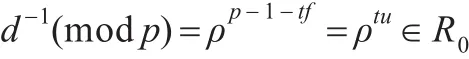


3 三次和四次剩余碼的冪等生成元


情況1 e0(α),e1(α),e2(α),e3(α)之中有一個為1,另外三個為 0。設 ei(α)=1,ei+1(mod4)(α)=ei+2(mod4)(α)=ei+3(mod4)(α)=0 。令e(x)=ei+1(mod4)(x)+ei+2(mod4)(x)+ei+3(mod4)(x)。顯然e(x)是冪等元。



4 結束語
本文給出了二元域上三次和四次剩余碼的冪等生成元表達式。求解這些冪等生成元與多項式xn-1最大公因式就可得到二元域上三次和四次剩余碼的生成多項式。而在有限域上求解兩個多項式的最大公因式可用已有的計算機軟件如Maple,Matlab等來解決,從而可得到具體的二元域上三次和四次剩余碼。如何確定更高次剩余碼的冪等生成元是一個有待研究的問題。
[1]Macwilliams F J,Sloane N J A.The theory of error-correcting codes[M].Amsterdam,the Netherlands:North-Holland,1977.
[2]Pless V,Qian Z.Cyclic codes and quadratic residue codes over[J].IEEE Trans on Inform Theory,1996,42(5):1594-1600.
[3]盧慧敏,董學東,李選海.Z2k上的二次剩余碼[J].應用數學學報,2008,31(2):257-265.
[4]董學東,高潔,楊麗.關于三次剩余碼[J].遼寧師范大學學報,2002,25(1):1-2.
[5]高潔.關于e次剩余碼[D].大連:遼寧師范大學,2002.
[6]高麗,李體政,封利鋒,關于四次剩余碼及其推廣[J].天津師范大學學報,2003,23(1):37-39.
[7]朱士信,陳安順.域F2上的三次剩余碼[J].電子學報,2008,36(12):2312-2314.
[8]Huffman W C,Pless V.Fundamentals of error correcting codes[M]. Cambridge:Cambridge University Press,2003:138-144.
二元域上三次和四次剩余碼的冪等生成元
董學東1,李文杰2,張 妍3
DONG Xuedong1,LI Wenjie2,ZHANG Yan3
1.College of Information Engineering,Dalian University,Dalian,Liaoning 116622,China
2.Middle School Attached to Chifeng College,Chifeng,Nei Mongol 024000,China
3.School of Mathematics,Liaoning Normal University,Dalian,Liaoning 116029,China
The generating polynomials of higher degree residue codes over finite fields are factors of the polynomialxn-1. Generally speaking,it is difficult to factor the polynomialxn-1over finite fields.This paper gives generating idempotents of cubic and quartic residue codes over the fieldF2.As a result,the generating polynomials of cubic and quartic residue codes over the fieldF2can be obtained by computing the greatest common divisors of these generating idempotents and the polynomial xn-1with computer software such as Matlab and Maple。
generating idempotent;residue code;cyclic code
有限域上高次剩余碼的生成多項式都是多項式xn-1的因式。針對多項式xn-1在有限域上分解的困難性,給出了二元域F2上三次和四次剩余碼的冪等生成元表達式。利用計算機軟件求解該冪等生成元與xn-1最大公因式就可得到三次和四次剩余碼生成多項式而不用分解xn-1。
冪等生成元;剩余碼;循環碼
A
TN911.22
10.3778/j.issn.1002-8331.1203-0577
DONG Xuedong,LI Wenjie,ZHANG Yan.Generating idempotents of cubic and quartic residue codes over fieldF2. Computer Engineering and Applications,2013,49(11):41-44.
國家自然科學基金(No.10171042);遼寧省教育廳高校科研項目(No.L2010234)。
董學東(1961—),男,博士,教授,研究領域:編碼密碼學;李文杰(1985—),女,碩士,研究領域:編碼密碼學;張妍(1978—),女,博士研究生,講師,研究領域:編碼密碼學。E-mail:dongxuedong@dl.cn
2012-03-26
2012-06-19
1002-8331(2013)11-0041-04

