基于統計過程控制技術的XBT 故障概率控制研究

方 芳 ,張 鵬，陳 晨

（1.國家海洋技術中心，天津 300112；2.中國煙草江蘇省公司揚州市公司，江蘇 揚州 225002）

投棄式溫度剖面測量儀（the Expendable Bathythermograph，XBT）是一種通過投棄在快速下降過程中感應海水溫度剖面的一次性使用的測量系統。它使用方便可靠，測量探頭成本低廉，并能進行大范圍實時溫度剖面數據的快速獲取，因此在海洋調查、海洋科考、海洋環境保護、海洋維權、海洋防災減災和國防建設等領域均有大量的應用需求。目前，國家海洋技術中心的技術人員已經攻克了投棄式剖面測量的相關關鍵技術，其測量指標已達到國外同類產品的水平，但海上試驗的成功率與國外產品相比還存在差距。本文基于這種情況，探討了一種利用統計過程控制技術分析XBT海上試驗故障的方法。

統計過程控制（Statistical Process Control，SPC）是應用統計技術對過程中的各個階段進行監控，從而達到改進與保證質量的目的[1]。這里統計技術是指任何可以用于分析和監控過程的統計方法。該種理論可以廣泛應用于設計、生產、服務和管理等一般過程。產品的實現過程總是存在波動的。統計技術可以幫助我們了解波動的特性和規律、分析引起波動的根本原因、尋找控制和減小波動的機會。按照統計學的原理，影響過程波動的原因可分為隨機因素（正常因素）和系統因素（異常因素）兩類。正常波動是指由隨機原因引起的、影響相對較小的、其影響是很難通過對過程控制而消除的、在技術上很難根本消除的或消除其影響要花費很大經濟代價的、正常的生產過程中允許存在的波動。異常波動是指由系統原因引起的、在生產過程中并不是大量存在的、一旦存在則影響比較顯著、比較容易查明和消除的、在正常的過程中不允許存在的波動。用統計規律判別和控制異常因素造成的質量波動，從而使過程處于受控狀態的方法稱為統計過程控制方法。

統計過程控制(SPC)技術作為測量數據處理的有效方法[2-3]，盡可能淺顯易懂地表達整個過程狀況，從而對整個過程的異常趨勢提出預警，以便管理人員及時采取措施，消除異常，恢復過程的穩定，從而達到和提高控制質量的目的。這種方法應用XBT海試結果的主要意義在于，在海試投放的過程中，故障概率總是存在著波動，而這正是我們發現問題并解決的突破口。分析引起波動的根本原因，辨別波動的起因是隨機因素還是異常因素引起的。如果波動是隨機因素引起的，其影響是很難通過技術從根本上消除的，這在試驗過程中是允許存在的波動。而異常波動在試驗過程中并不是大量存在的，而一旦存在則影響比較顯著、比較容易查明和消除的，這為找到XBT故障的原因提供依據。

1 XBT系統現場試驗結果的統計分析

根據2009—2010年XBT系統的海試報告進行歸納，故障原因的歸納是基于報告中的結論來表述的。如表1～表4所示。

2 XBT系統現場試驗結果分析

2009—2010年間的4次海試，共進行了19組試驗，合計投放126枚測量探頭，其中50枚出現故障，故障概率為0.397，詳見表5。

對海試報告得到的試驗故障現象進行歸納，見表6。

從表6中可以清晰地看出，由于漆包線的問題導致系統出現故障的概率達到了72%。

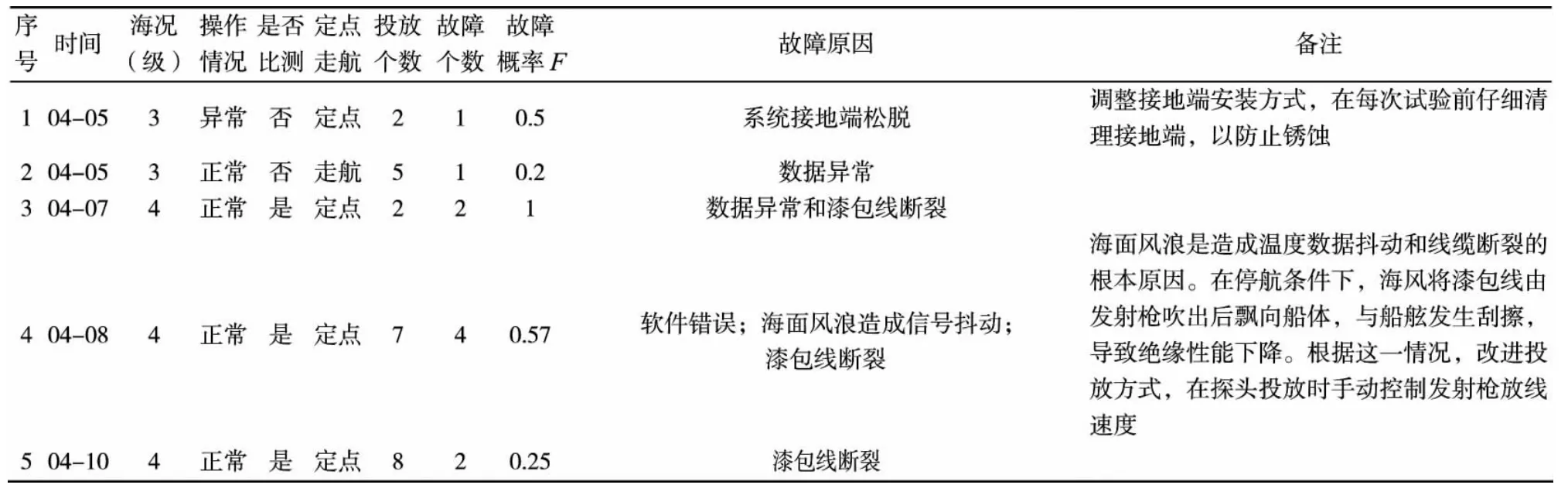
表1 2009年第一航次海試結果統計

表2 2009年XBT 第三方獨立檢測結果統計

表3 2009年第二航次海試結果統計

表4 2010年海試結果統計

表5 故障概率統計表

3 過程統計控制（SPC）技術分析現場試驗數據的探討

過程統計控制（SPC）技術的基本要求是抽取的樣本來自于同一總體。而在XBT系統現場試驗結果的歸納中，存在著由于各航次及各試驗階段所使用的探頭，存在著不同程度的零部件的改進、工藝改進、海況和操作不同的情況，因此使用簡單的統計方法計算故障概率存在試驗條件不統一的問題。因此，首先使用了工程加權法[3]處理現場試驗結果，以排除試驗條件的影響。該方法的核心思想是對不同條件下的海試結果增加加權因子，將歷次海試結果修正到相同的評價條件下，以盡量符合相同的試驗條件，達到滿足SPC技術分析現場試驗數據的要求。考慮到在歷次海試中，海況良好，定點投放的情況較多，因此，設定探討基于如下的評價條件：（1）投放環境按海況三級，天氣良好；（2）投放水平嚴格按照XBT操作流程進行；（3）是否在同一站位相近的時間進行了XBT/CTD的比測試驗；（4）投放方式為定點投放；（5）投放個數最少為10枚；（6）技術水平設定為采用改進的零部件。

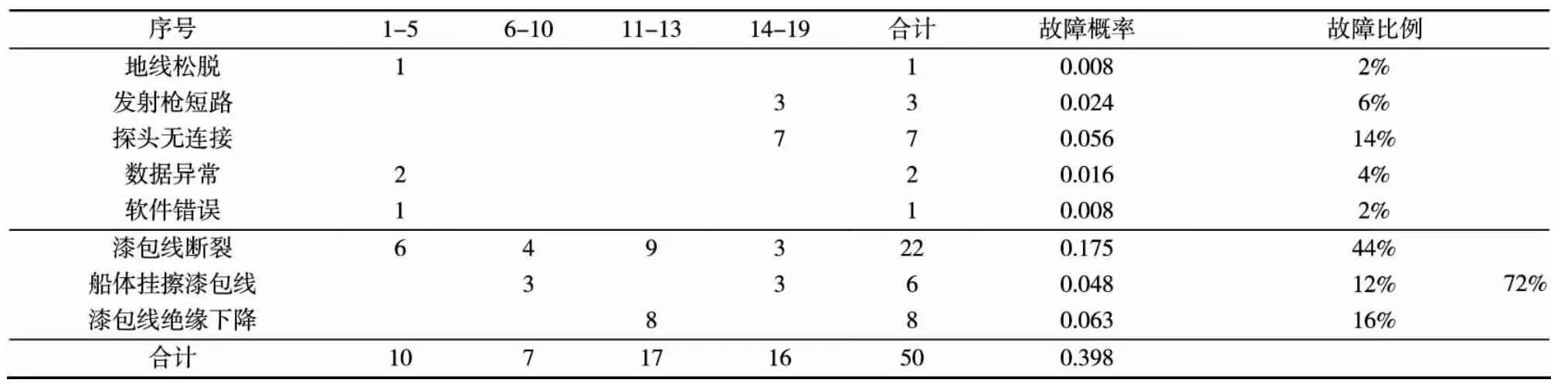
表6 故障現象統計表

3.1 確定各加權因子Ki

加權因子由以下幾個方面組成：

（1）環境因子K1：海況不同、天氣狀況不同投放成功率不同，海況和天氣越惡劣，系統故障概率越高，K1取值越小。

（2）操作因子K2：操作是否按照操作規范進行，規范與否造成投放故障概率也不同。操作隨意性越大，系統故障概率越高，K2取值越小。

（3）比測因子K3：進行比測的數據較為準確，而未進行比測的數據僅憑主觀判斷，往往出現判斷失誤的情況，因此K3取值較大。

（4）投放方式因子K4：走航方式造成系統故障概率越高，K4取值越小。

（5）投放個數因子K5：投放個數小于10個，得出的故障概率沒有說服性也失去普遍性，因此K5取值越小。

（6）技術水平因子K6：未改進零部件的系統投放成功率越低，因此K6取值越小。

因子的量值可以采用專家評分法，一般取值0.1～10。標準情況下總加權因子Wi定義為各加權因子之積，如公式（1）所示：

則統一條件下的故障概率F’為：

3.2 重新修正的結果

按照以上的方法，依據公式（1）、公式（2），按照海試的時間順序，對海試的實際故障概率數據進行重新計算并排序，如表7所示。

在SPC分析過程中使用休哈特先生發明的控制圖[4]，它利用概率統計原理，做出帶有控制界限的曲線圖，該曲線由按照時間順序抽取的數據所得的特性值組成，能夠反映過程的趨勢。每個抽取的數據在過程控制中稱為子組。控制圖是由縱軸和橫軸構成的簡單坐標圖。橫軸表示子組號，縱軸表示過程特征值。按照各樣本點形成的自然順序（時間先后），將其逐一繪制在坐標圖中，并順序連接為相互銜接的折線，由此形成一張控制圖。控制圖中還包括3條重要的線，分別是中心線(Central Line,CL)，以及中心線兩側的上控制界限(Upper Control Limit,UCL)和下控制界限(Lower Control Limit,LCL)。中心線代表所點繪特性值的基準值，一般為所考察數據的平均值。而上下控制界限分別位于中心線兩側的3σ 距離處。其中，σ 為所點繪統計量的總體組內標準差，也可用子組標準差進行估計。3σ 控制界限表明若過程處于統計控制狀態，則大約有99.7%的子組值將落在控制界限之內。

表7 海試結果重新統計分析表

控制圖的種類是多種多樣的，在本文中使用的控制圖是計數控制圖中的一種——p 控制圖。p 控制圖是一種基于二項統計分布的計數型控制圖，它繪制的是每個樣本的不合格率。其中二項分布是以Bemoulli試驗為依據[5]，每個試驗都將產生兩個可能的輸出，即“通過”和“不通過”。而樣本的試驗必須滿足以下的條件：（1）每個試驗應是獨立的，一次試驗的輸出不能影響另一次試驗的輸出；（2）對于每個試驗來說，只能有兩個可能輸出中的一個輸出；（3）樣品的試驗數必須是正整數；（4）對所有試驗來說，成功或者故障的概率必須是相同的。

滿足以上的條件，得到控制限公式如表8所示。

每個子組樣本可以有相同的樣本量或者不相同的樣本量。若子組大小隨子組不同而發生變化，則對于每個子組都要計算出各自單獨的控制界限。

按照上述方法，進一步分析海試結果。首先現場試驗的結果服從成功或者故障這兩種不連續的輸出，且投放探頭的故障概率是相同的，服從二項統計分布，符合p 控制圖的使用條件，其中繪制的是每個子組中的故障概率。

首先將按照時間順序排列的序號作為子組號，將上文重新處理的統計表進行重新歸納，如表9所示。

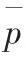
由于各組樣本量大小不同，因此對每個子組按照表中p控制圖的上控制限(UCL)和下控制限(LCL)公式計算，計算得出海試結果UCL及LCL統計表如表10所示（其中UCL得到大于1的值，一律按照1計入表中；LCL得到小于0的值，一律按照0計入），畫出p 控制圖如圖5所示。

表8 p 控制圖的控制限公式

表9 海試結果故障率分析

根據上面的分析，可以發現，由于各組的樣本量不同，因此分別繪制上下限非常費時，這時考慮修正過且處理后的故障概率，由于在對實際的故障概率處理時，考慮到了投放個數因子，處理后的故障概率假設為每個子組投放個數為10個，因此對處理后的概率重新繪制p 控制圖，求處理后故障概率平均值：

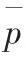
取各子組的平均樣本大小n=10，重新標繪p 控制圖的上下限，如下：

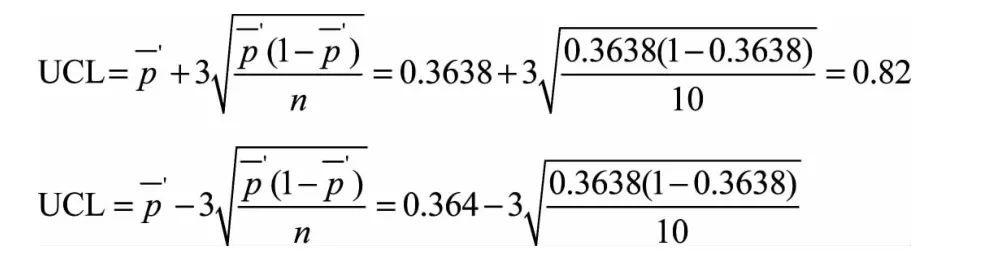
計算得到的LCL值為負值，以0計。

得到修正后的p 控制圖，如圖6所示。

以國產XBT系統目前的制造水平及設計水平，故障概率的上限為82%，雖然現場數據分析的結果以及預計的結果均處于上限范圍之內，但也可以判斷，除了隨機因素（比如天氣惡劣因素，人員使用不當等）是造成系統成功率不高的原因之外，切實提高系統本身的固有可靠性才是提高系統成功率的根本，尤其是在海試現場中表現較為明顯的由于漆包線、探頭殼體、發射槍的制造工藝問題造成的故障，是值得我們進一步分析改進的。

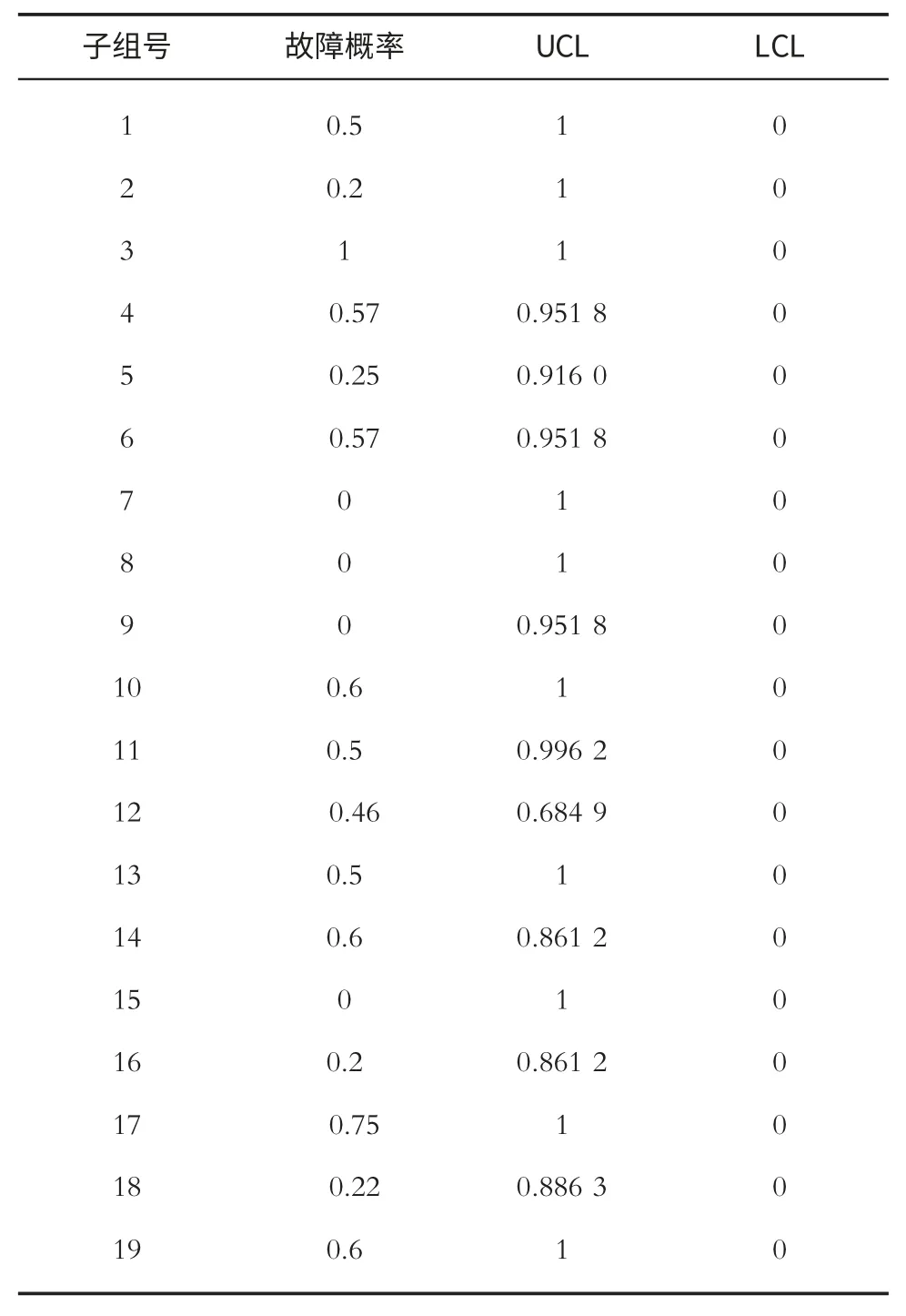
表10 海試結果UCL 及LCL 統計表

另外，要注意的是，由于每階段投放探頭數量約在5～8枚左右，試驗樣本數量較少，各項比測和一致性檢驗不足以反映XBT系統性能的真實情況成為進行SPC控制的一大障礙。

圖5 海試結果p 控制圖

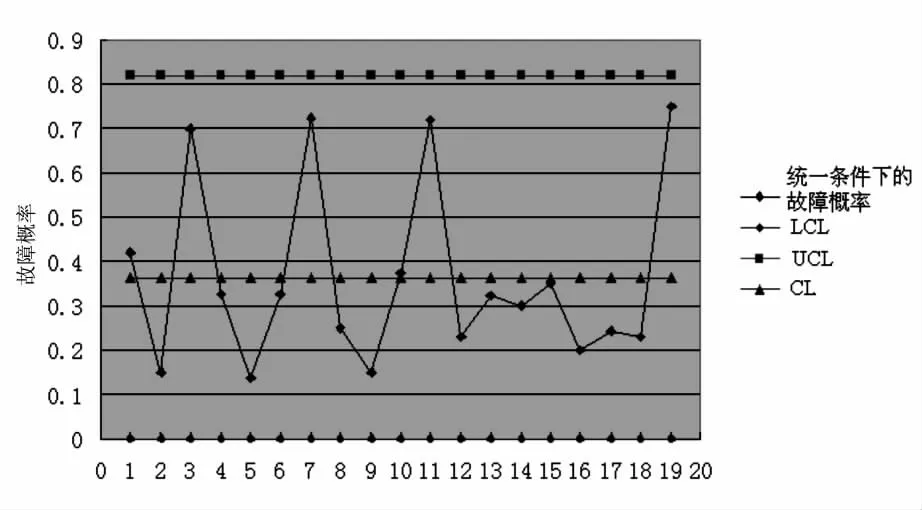
圖6 修正后的p 控制圖

4 結語

將統計過程控制的方法應用于XBT海上試驗的故障概率控制中來，一方面對歷年的投放故障概率情況進行了監控，另一方面也從中區分出故障概率的隨機波動、異常波動，從而分析出XBT投放故障概率波動的范圍（即上下限）、平均值以及故障概率波動的原因，找到XBT投放出現故障的因素。分析證明，該方法對于研究XBT的海上試驗的故障概率控制具有一定的意義。

[1]張增照.以可靠性為中心的質量設計、分析和控制[M].北京:電子工業出版社,2010:296-297.

[2]鐘倫燕.統計過程控制(SPC)技術原理和應用[M].北京:電子工業出版社，2000:12-13.

[3]陳炳生.電子設備可靠性工程系統設備的可靠性理論與實踐[M].北京:國防工業出版社,1987:95-97.

[4]國家質量技術監督局.GB/T 4091-2001.常規控制圖[S].北京:中國標準出版社,2001.

[5]中國國家標準化管理委員會.GB/T 4087-2009.數據的統計處理和解釋二項分布可靠度單側置信下限[S].北京:中國標準出版社,2009.