基于遺傳神經網絡的高速公路縱坡運行速度預測方法研究
靳燦章,候志峰,徐桂興,楊朝輝
(天津市市政工程設計研究院,天津市 300051)
0 前言
目前,公路線形設計的基本依據是設計速度,它決定了公路幾何線形的各項要素。設計速度是一固定值,其作為基礎參數,規定了某一路段的最低設計標準,設計中只要一條公路所采用的最低指標大于其設計速度對應的最低指標,就認為該設計符合要求。經過多年的設計實踐,發現這種設計速度的方法存在諸多不足之處,主要表現在:(1)線形設計要素與實際行車速度不相容;(2)線形設計要素之間不相容;(3)線形的行車速度標準不一致。為此,《公路路線設計規范》(JTG D20-2006)對線形設計引入了運行速度檢驗的概念,運行速度考慮了絕大多數駕駛員的交通心理需求,是車輛的實際運行速度,以其作為線形設計參數,可以消除現行設計方法的不足,有效地保證了線形相關指標與速度的相容性,可以獲得連續一致的均衡設計。
不同車輛的運行速度各不相同,但運行速度值一般呈正態分布,通常以小客車在車速分布累計曲線上第85位百分點的速度來表示運行速度,即V85。
運行速度是車輛實際行駛的速度,在公路建成之前無法實測獲得。因此,應用運行速度作為設計參數進行線形設計或設計成果檢驗的關鍵就是運行速度的預測。而運行速度又受人、車、路及周圍環境等多種因素的影響。本文通過對高速公路不同縱坡路段運行速度的調查,研究在自由流運行條件下,公路縱斷面線形指標(主要指坡度i與坡長S)與高速公路運行速度的相關關系,運用遺傳神經網絡的方法來預測高速公路縱坡運行速度的方法。
1 算法介紹
BP(back-propagation)算法作為一種神經網絡訓練方法,由于其理論依據扎實,推導嚴謹,物理概念清晰,目前仍是應用最為廣泛的神經網絡模型之一。但是,該算法學習收斂速度慢,得到的網絡性能較差。
遺傳算法通過模擬自然界的進化過程來迭代產生適于解決問題的優化解,其搜索機制中的隱含并行性使得搜索過程能不斷向全局最優解逼近。遺傳算法具有:自組織、自適應和自學習性(智能性),并且在本質上具有并行性;遺傳算法不需要求導,只需要影響搜索方向的目標函數和相應的適應度函數。
將BP神經網絡與遺傳算法結合起來,取長補短,能有效解決很多一般數學方法難以解決的問題。遺傳神經網絡模型的總體結構如圖1所示。
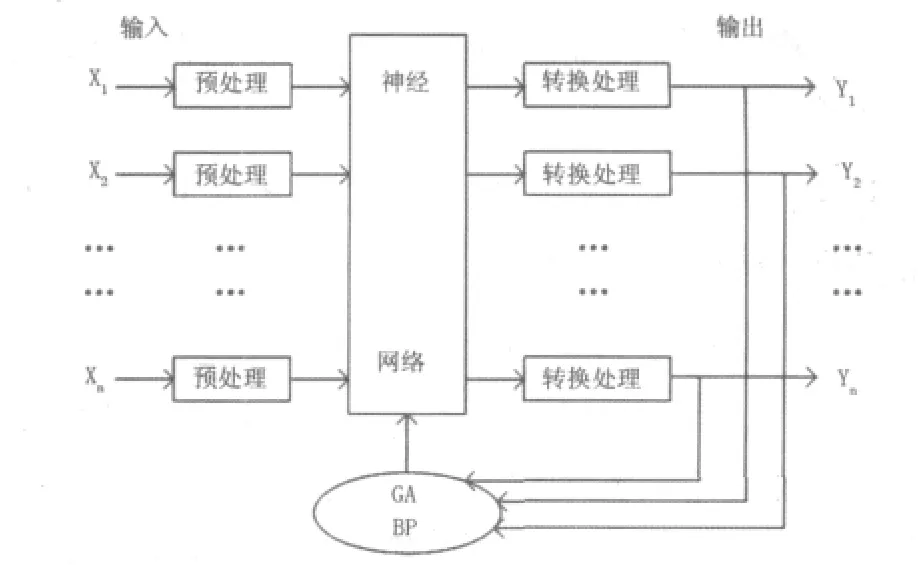
圖1 遺傳神經網絡預測模型功能框圖
1.1 遺傳算法優化神經網絡的結構
(1)個體編碼。采用二進制編碼形式,確定隱含層神經元個數的空間大小,對遺傳染色體進行編碼操作,每一條染色體個體對應著隱含層神經元個數的一種取值。
(2)初始化。隨機產生一定數目的個體組成初始種群。
(3)計算適應度。設網絡輸入N次信號,輸出n次正確解,則適應度函數為:f=n/N。適應度函數f在[0,1]區間內,其中f值越接近1的個體,其輸出信號的正確率就越高。
(4)遺傳操作的確定。首先將當代種群的個體按適應度由大到小排序,然后選擇一定的下位個體將其淘汰,淘汰率一般為30%;在上位個體中實行均勻交叉,生成的子個體填補到種群中,以保持種群的規模不變。最后實行變異操作,生成子代種群。
1.2 遺傳算法優化神經網絡的權值
(1)個體編碼。將神經網絡各層之間可能存在的連接權值編碼成實數碼串或者二進制碼串,每條碼串中包含著網絡中的所有權值,其排列順序可以自定,組成一個染色體。
(2)初始化。隨機產生一定數目的碼串個體組成初始種群。
(3)計算適應度。設網絡共有M個訓練樣本,讓所有的訓練樣本依次通過解碼后生成的神經網絡,計算所有訓練樣本一次通過的平均總誤差作為每條染色體的適應度,如公式:
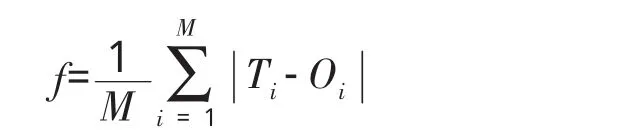
式中:Ti——實測值(即縱坡實測運行速度值);
Oi——網絡的輸出值。
(4)遺傳操作的確定。將選出的染色體進行單點交叉,然后隨機產生一小的概率對隨機選中的一部分染色體個體碼串進行變異操作。為了克服遺傳算法的“早熟”現象,可以在算法進行初期采用較小的變異概率,在算法運行一段時間后,采用較大的概率,加快染色體的變化程度,保持種群個體的多樣性。
2 運行速度與高速公路縱坡線形指標遺傳神經網絡模型的建立
影響縱坡運行速度值的線形指標主要是坡度i與坡長S,本文選擇坡度i、坡長S、縱坡初速度Vin三個參數為輸入參數,實測縱坡出口速度Vout為輸出參數。采用遺傳神經網絡的原理,以大量實測小客車高速公路縱坡運行速度值(V85)建立上、下坡學習樣本。上坡與下坡學習樣本、實測值、網絡輸出值分別如表1、表2所示。
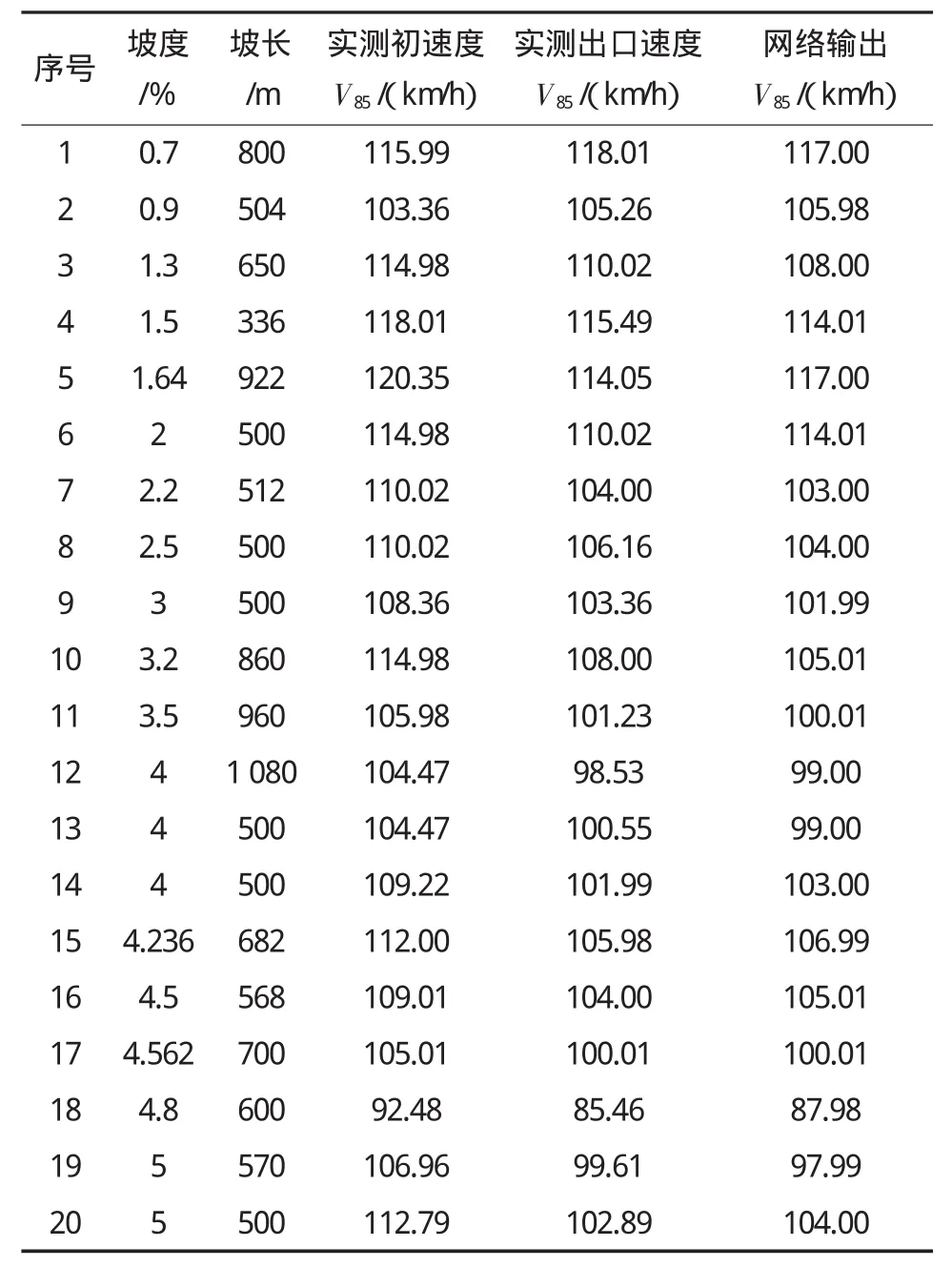
表1 上坡網絡學習樣本及預測值

表2 下坡網絡學習樣本及預測值
利用Matlab神經網絡工具箱函數,先將輸入數據利用premnmx函數進行歸一化處理,并用很小的隨機數對每一層的權值初始化,以保證網絡不被大的加權輸入飽和。網絡期望誤差最小值為0.002,最大訓練次數為8 000,利用遺傳算法對神經網絡進行優化,本文略去了網絡的具體實現過程,只給出了結果如圖2、圖3所示。網絡訓練結束后,對網絡的輸出(歸一后的預測值)進行恢復,得到了網絡的實際輸出,見表1、表2。可以看出,最大誤差為3.83%,網絡的訓練精度非常高。
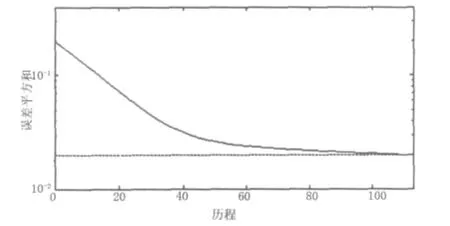
圖2 網絡訓練誤差變化曲線
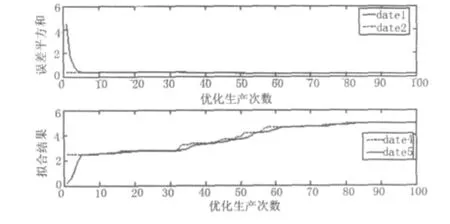
圖3 遺傳算法優化神經網絡
3 高速公路縱坡運行速度的預測
在表1、表2中分別用其中4個樣本為檢測樣本,其余作為訓練(學習)樣本,網絡模型、參數均不變,可預測不同坡度和坡長下的運行速度值,預測結果詳見表3。由表3中的數據可以看出,預測最大誤差在7%左右,證明遺傳神經網絡模型的預測精度較高,可用此模型預測不同縱斷面線形指標的運行速度,從而指導線形的評價、修改。
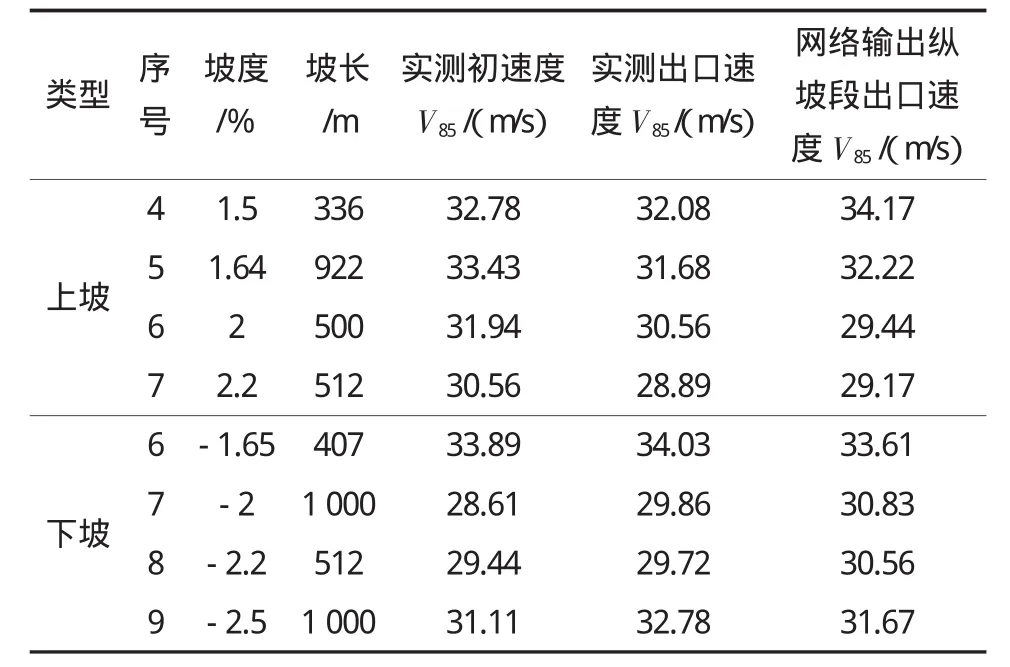
表3 運行速度預測結果對比表
4 結論
遺傳神經網絡具有很高的非線性處理能力,借助MATLAB的工具箱較易實現程序的編寫。通過遺傳神經網絡可以建立運行速度與高速公路縱斷線形指標之間的關系模型,用此模型可以估算新建或已建高速的縱坡車速,其結果較為可靠。這將對推廣采用運行速度的設計方法有一定的參考價值。
[1]JTG D20-2006,公路路線設計規范[S].
[2]周榮貴.公路縱坡坡度與坡長限制的研究[D].北京:北京工業大學,2004.
[3]VELASCO JR,MAGDALENA L.Genetic algorithms in fuzzy control systems[A].WINTER G W.Genetic algorithms in Engineering and Computer Science[C].Great Britain:Academic Press,1995.141-165.
[4]GRUAU F.Genetic microprogramming of neural networks[A].KOZA J T.Genetic programming[C].New York:Oxford University Press,1994.495-517.

