質(zhì)量矩控制自旋彈彈體性能分析

高長生，張研，魏鵬鑫，荊武興

(哈爾濱工業(yè)大學航天工程系，黑龍江哈爾濱150001)

0 引言

質(zhì)量矩和舵是大氣層內(nèi)導彈的兩種控制方式，與后者相比質(zhì)量矩的優(yōu)點［1-3］是:(1)氣動外形良好;(2)抗燒蝕能力強［4］。缺點是:(1)內(nèi)部需要活動部件，布局設計較難;(2)滑塊運動引起慣性力大［5］。

前人通過研究得出慣性力及力矩對STT導彈彈體性能的影響很小，驗證了慣性力及力矩在STT導彈上應用的可行性。而實現(xiàn)質(zhì)量矩技術在自旋彈上的應用存在很多難點問題［6］。不同于舵面很輕可以忽略其動態(tài)特性的舵控制導彈，質(zhì)量塊運動的動態(tài)特性不能忽略。為了提高控制系統(tǒng)跟蹤制導指令的能力，活動質(zhì)量塊必須頻繁往復運動，因而產(chǎn)生的慣性力將嚴重地影響著系統(tǒng)的動態(tài)品質(zhì)，降低了系統(tǒng)的性能［7］。

本文研究了滑塊運動產(chǎn)生的慣性力對自旋彈的影響問題。首先將慣性力進行分類;然后分析了每類慣性力產(chǎn)生機理;最后研究了如何降低慣性力的負面效應。

1 問題描述

本文所研究的質(zhì)量矩控制自旋彈采用單滑塊的控制方式，其布局構型如圖1所示。飛行器由彈體B和徑向滑塊p組成，滑塊p的導軌平行于彈體坐標系Oxbybzb的yb軸。對于舵控制導彈而言，舵面做與彈旋同頻率的正弦偏轉(zhuǎn)運動可以對旋轉(zhuǎn)飛行器產(chǎn)生控制力，這里滑塊也按正弦運動進行。已有文獻研究該類運動時未考慮滑塊慣性力對系統(tǒng)的影響，因而系統(tǒng)是可控的。實際系統(tǒng)中必須考慮慣性力的影響，本文研究發(fā)現(xiàn)，慣性力的存在使系統(tǒng)難以保持良好的彈體特性。

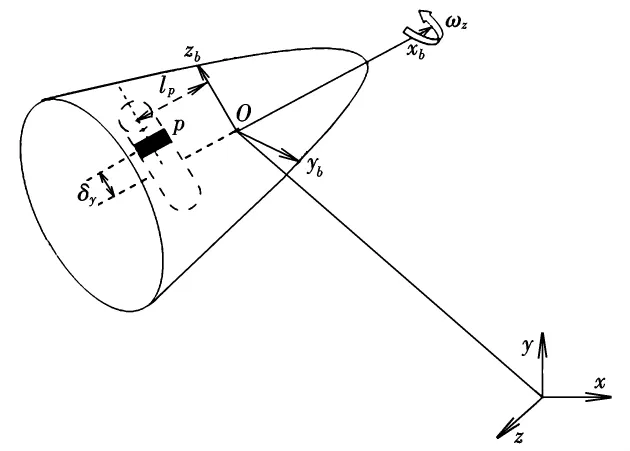
圖1 質(zhì)量矩基本構型圖

通過仿真分析驗證了慣性力對自旋彈的影響。圖1中滑塊導軌遠離彈體質(zhì)心，這是公開文獻普遍應用的自旋彈研究對象。該對象的彈體姿態(tài)響應會出現(xiàn)發(fā)散的情況，其準迎角的響應情況如圖2所示。準側(cè)滑角響應情況也類似。

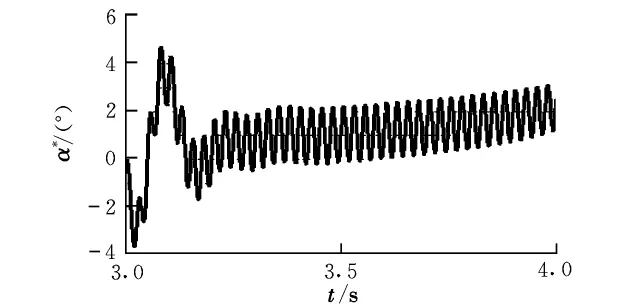
圖2 滑塊持續(xù)正弦運動時自旋彈姿態(tài)響應

圖2說明當導彈的總體參數(shù)選擇不當時，在氣動力和伺服電機的共同作用下，導彈為非保守系統(tǒng)，其準迎角與側(cè)滑角會出現(xiàn)發(fā)散現(xiàn)象。下面將分析產(chǎn)生這種發(fā)散現(xiàn)象的原因。

2 質(zhì)量矩控制導彈慣性力分類

彈體B、滑塊p和總系統(tǒng)S的質(zhì)量之間的關系為:mS=mB+mp;定義滑塊p的質(zhì)量比為:μp=mp/mS。定義彈體相對于地面坐標系的角速度為ω1=［ωxωyωz］T，彈體質(zhì)心的速度為 V1，滑塊p在彈體內(nèi)的位置矢量為:rbp=［lpδy0］T。其中，lp為滑塊p的軸向坐標;δy為滑塊p的橫向偏移量。則系統(tǒng)質(zhì)心在彈體內(nèi)的位置矢量為:

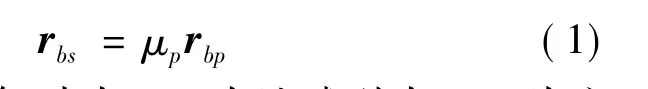
定義R1為空氣動力;GS為地球引力;MS為空氣動力對彈體質(zhì)心b的氣動穩(wěn)定力矩;Md為阻尼力矩。質(zhì)量矩操縱力矩Mc為:

彈體對質(zhì)心b的轉(zhuǎn)動慣量矩陣為:

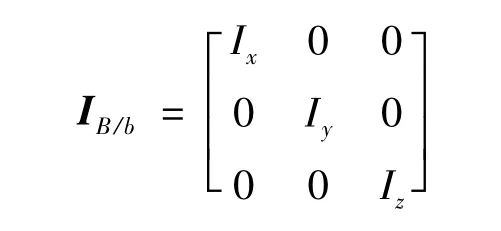
則飛行器質(zhì)心運動和繞質(zhì)心轉(zhuǎn)動的動力學方程可表示為:

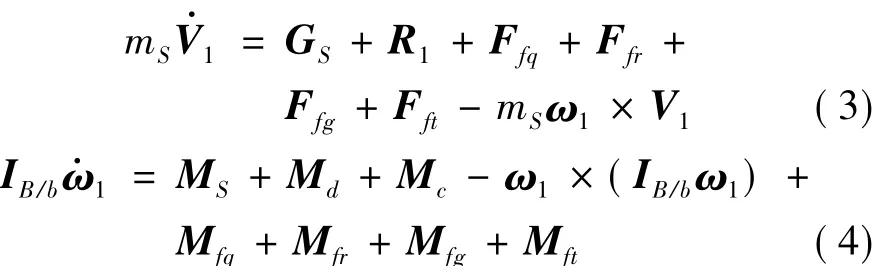
定義各個慣性力及慣性力矩如下:

(1)Ffr=為活動質(zhì)量體伺服運動對彈體施加的反作用力，稱為附加相對慣性力;

Mfr=－(rbp－rbs)×為Ffr對系統(tǒng)質(zhì)心施加的作用力矩，稱為附加相對慣性力矩。

(2)Ffq=

×rbp為由于彈體的角加速度運動，活動質(zhì)量體對彈體施加的切向反作用力，稱為附加切向慣性力;

Mfq= －(rbp－rbs)× rbp為 Ffq對系統(tǒng)質(zhì)心施加的作用力矩，稱為附加切向慣性力矩。

(3)Ffg=－2mpω1為由于活動質(zhì)量體運動在彈體旋轉(zhuǎn)角速度下對彈體施加的反作用力，稱為附加哥氏慣性力;

Mfg=－(rbp－rbs)×(2mpω1×為 Ffg對系統(tǒng)質(zhì)心施加的作用力矩，稱為附加哥氏慣性力矩。

(4)Fft= －mp［ω1×(ω1×rbp)］為由于彈體姿態(tài)運動，活動質(zhì)量體離心運動對彈體施加的反作用力，稱為附加離心慣性力;

Mft= －(rbp－rbs)×mp［ω1×(ω1×rbp)］為 Fft對系統(tǒng)質(zhì)心產(chǎn)生的作用力矩，稱為附加陀螺慣性力矩。

3 慣性力對彈體性能的影響能力分析

設滑塊的正弦運動規(guī)律為:

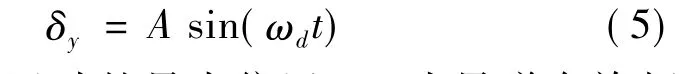
式中，A為滑塊運動的最大位置;ωd為導彈自旋頻率。則各個動態(tài)慣性力矩在準彈體系下的分量分別為:

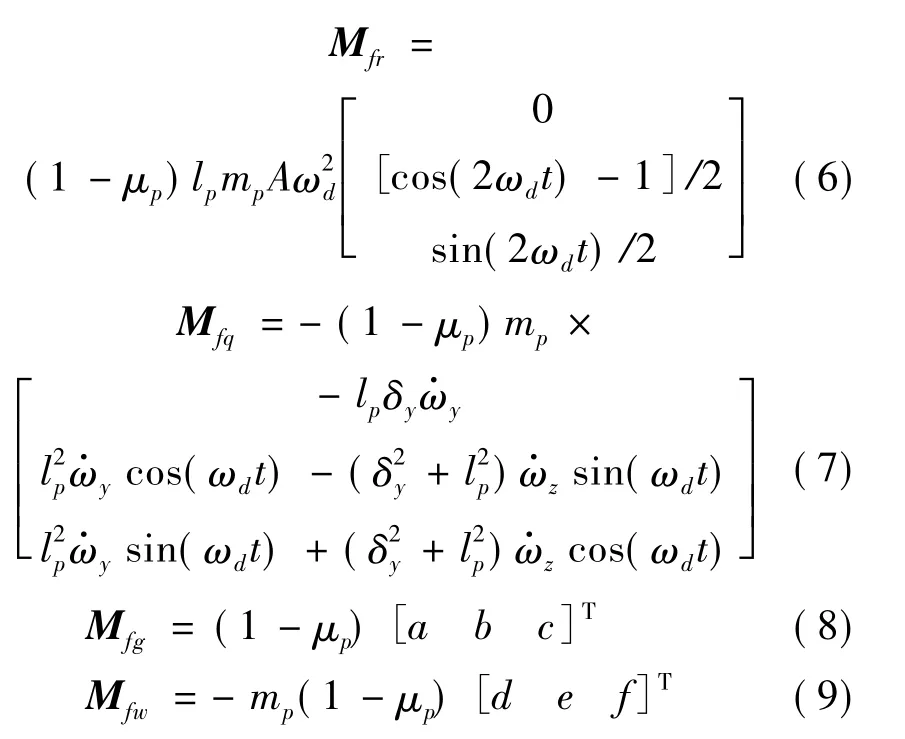
其中:

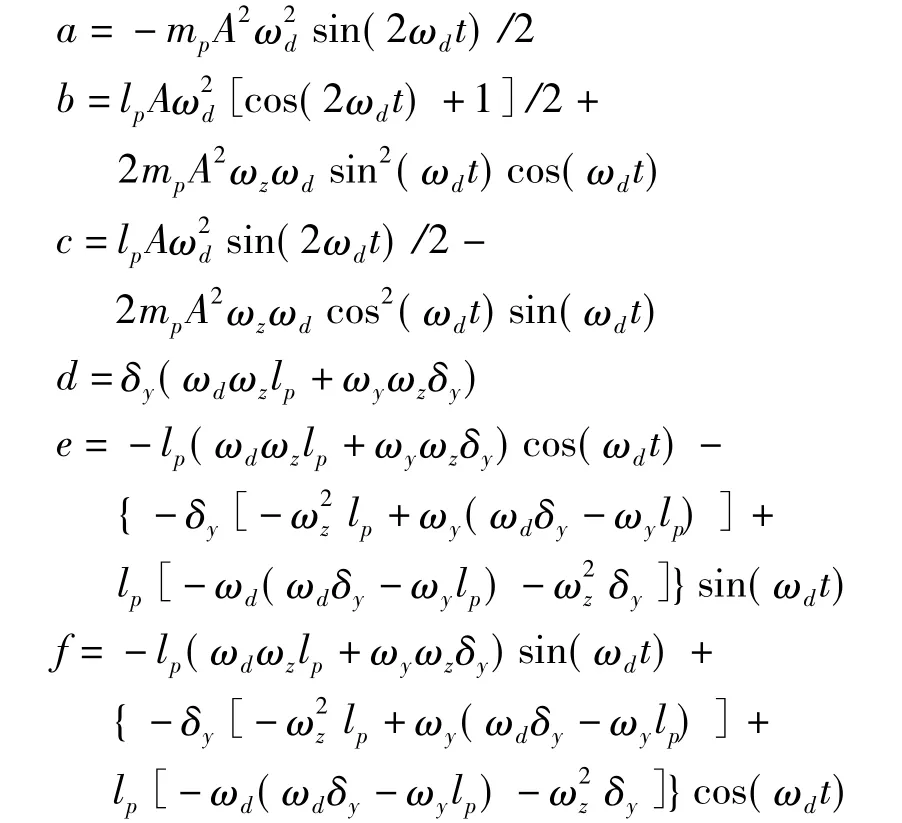
通過數(shù)值仿真，將影響姿態(tài)運動各力矩在準彈體系下進行分解，圖3給出了各力矩在準彈體系y軸上的分量。從圖中可以看出，在俯仰方向上，各動態(tài)力矩雖然呈周期性變化，但并不是所有的動態(tài)力矩的周期平均力矩均為零，系統(tǒng)總慣性力矩均值也不為零。各個動態(tài)力矩均值(單位為N·m)為

其中，Msw和Mfq的平均力矩較小，與其它力矩相比可忽略。Mfr，Mfg和Mfw的周期平均值都要大于操縱力矩 Mc。

仿真結(jié)果表明:(1)慣性力是影響自旋彈彈體特性的主要因素，當動態(tài)慣性力矩平均效果大于系統(tǒng)操縱力矩時，系統(tǒng)將會出現(xiàn)發(fā)散現(xiàn)象;(2)由于該分析是針對典型布局形式開展工作的，因此結(jié)果具有一定的普遍性;(3)解決慣性力的負面影響問題，首先是優(yōu)化彈體內(nèi)部結(jié)構布局，降低該力的影響，在此基礎上設計魯棒性強的控制律。

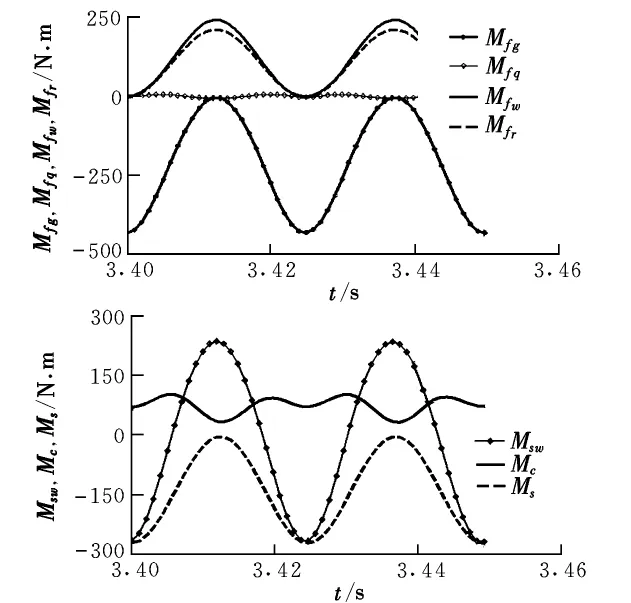
圖3 各動態(tài)力矩在y軸方向的分量

本文從總體布局角度分析如何降低慣性力的影響。為了使系統(tǒng)可控，必須消除各慣性力矩的平均效果。從式(6)～式(9)可知，取lp=0，即滑塊導軌與彈體橫向慣性主軸重合，在假設角速度分量ωy，ωz和ω·z為定值時，各動態(tài)慣性力矩在一個周期內(nèi)的平均力矩表達式為:

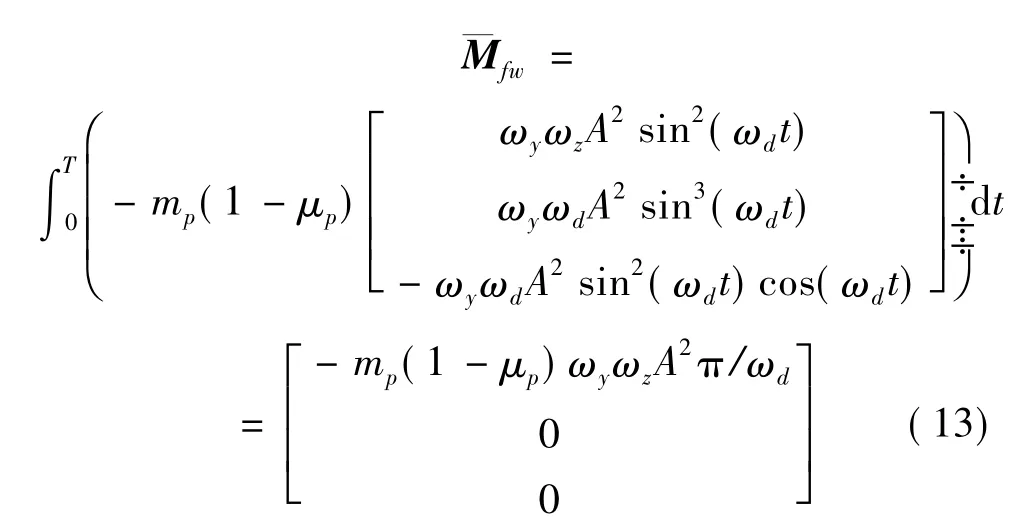
由式(10)～式(13)可知，當lp=0時，各慣性力矩對導彈俯仰和偏航姿態(tài)的平均效果為零。這種情況下，質(zhì)量矩控制的平均效果是由氣動操縱力矩來產(chǎn)生的，這與STT導彈的質(zhì)量矩控制原理類似。此時系統(tǒng)的姿態(tài)響應如圖4所示。

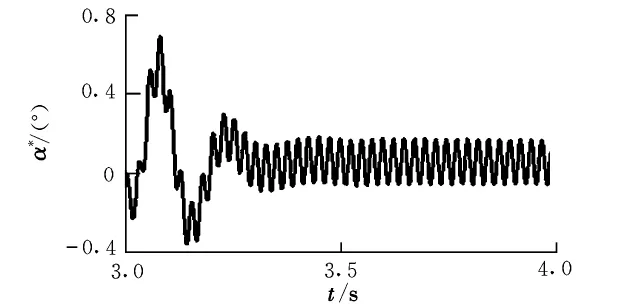
圖4 慣性力影響較小時彈體姿態(tài)響應

從圖中可以看出，當滑塊導軌與彈體橫向慣性主軸重合時，可以減小慣性力矩對自旋彈姿態(tài)的影響，使得飛行器的姿態(tài)變化為一個穩(wěn)態(tài)的響應過程。滑塊的等效運動會產(chǎn)生一個彈體需要的準側(cè)滑角。

4 結(jié)束語

本文研究表明:切向慣性力和離心慣性力的變化導致導彈慣性主軸頻繁偏移;導彈自旋一周后哥氏慣性力和相對慣性力對彈體的等效控制力不為零，它們是影響系統(tǒng)性能的重要因素。

慣性力是影響質(zhì)量矩在自旋彈應用的難點問題，其大小與導彈總體參數(shù)密切相關，為了降低慣性力的影響，提高系統(tǒng)控制能力，應該深入研究導彈總體布局問題。降低滑塊導軌與導彈橫向慣性主軸之間的距離可有效降低慣性力對系統(tǒng)的影響。當然，完全降低慣性力的負面影響是不可能的，還應從控制角度進行研究。本文從消除慣性力負面影響的角度進行研究，若充分利用總體設計技術，從利用慣性力正面影響角度去研究也是一種途徑，這也是今后的努力方向。

［1］Kumar K D，Zou A M．Attitude control of miniature satellites using moving masses［C］//SpaceOps 2010 Conference．Huntsville，Alabama，April 25-30，2010．

［2］Mukherjee R M，Balaram J．Attitude dynamics and control of moving mass multi body aeromaneuver vehicle［C］//Atmospheric Flight Mechanics Conference and Exhibit．Honolulu，Hawaii，August18-21，2008．

［3］Vaddi SS，Menon P K，Sweriduk G D．Multi stepping approach to finite-interval missile integraed control［J］．Journal of Guidance，Control，and Dynamics，2006，29(4):1015-1019．

［4］Menon PK，Sweriduk G D，Ohlmeyer E J，etal．Integrated guidance and control of moving-mass actuated kinetic warheads［J］．Journal of Guidance，Control，and Dynamics，2004，27(1):118-126．

［5］李瑞康，高長生，荊武興，等．飛行器變質(zhì)心控制及性能分析［J］．宇航學報，2010，31(9):2165-2171．

［6］Yam Y，Mingori D L．Stability of a spinning axisym metric rocket with dissipative internal mass motion［J］．Journal of Guidance，Control，and Dynamics，1997，20(2):306-311．

［7］廖國賓，于本水，楊宇光．質(zhì)量矩控制技術的機理分析及方程簡化研究［J］．系統(tǒng)工程與電子技術，2004，26(11):1635-1639．