基于設計結構矩陣的目標級聯優化規則

徐 川，姚錫凡，楊 屹

（華南理工大學 機械與汽車工程學院，廣東 廣州 510640）

當今產品的系統設計走向復雜化，大規模化和多學科交叉化，而大規模復雜系統設計通常是層次系統和非層次系統的混合系統。目標級聯法（Analytical Target Cascading，ATC）是分解層次系統的有效優化方法，但是對于混合系統，如果分解不當就會造成父系統與子系統、子系統與子系統之間的信息交互聯系過多，增加TC的分解迭代次數，從而難以實現系統之間的協同優化[1]。設計結構矩陣（Design Structure Matrix，DSM）是用于產品開發過程進行規劃和分析的矩陣工具，對于分解非層次的耦合系統非常有效[2]。因此，將DSM和ATC方法結合，得出解決層次系統和非層次系統的混合系統的基于DSM的TC優化方法。

1 目標級聯法

目標級聯法 （TC），又稱目標級聯分析法（Analytical Target Cascading，ATC），是用于解決多層次系統的一種多學科設計優化方法。1999年由Michelena、Kim和Papalambros等人提出至今，TC應用范圍不斷加大，優化計算效率也不斷提高。TC方法是一種非集中式的分解協調多學科優化方法，它按照對象功能或模塊等將需要研究的問題分解成層次結構（見圖1），允許層次結構中的各元素（子系統）自主決策，父代元素對子代元素（子代系統）的決策進行協調以使問題的目標最優化。其特征之一是目標級聯，即系統中的父級系統為子系統設置目標并將目標傳遞給子系統，另外一個特征是分析，即子系統都有一個分析模塊來計算子系統的響應。

圖1（a）將優化系統分解為system-subsystem-component 3個層次。將 system、subsystem和 component統稱為元素（element），圖 1（c）為第 i層第 j元素 Eij與上層和下層信息交換圖。在TC規劃過程中，系統級的性能指標或目標值一旦確定，其下層各級元素的指標或目標值將逐級經轉換得到[3]。目標值的轉換過程是一個由上至下逐層分解的過程，該過程要求各層之間及同層元素之間能夠在一定的可控范圍內相互協調，如果所有目標值均到達要求，那么整個系統目標也將在某種優化程度上得到滿足，這一過程如圖1（b）所示。

2 設計結構矩陣

設計結構矩陣由Steward博士提出后，經過改進從簡單DSM到分層DSM，現在廣泛用于復雜產品設計的任務簡化和優化。DSM是一個排列順序相同的n階方陣，其維數表示設計任務的個數，對角線上的元素表示設計任務本身，其余元素為0或1，表示設計任務之間的信息聯系關系。“0”表示相互之間沒聯系，“1”表示相互之間有聯系[4]。

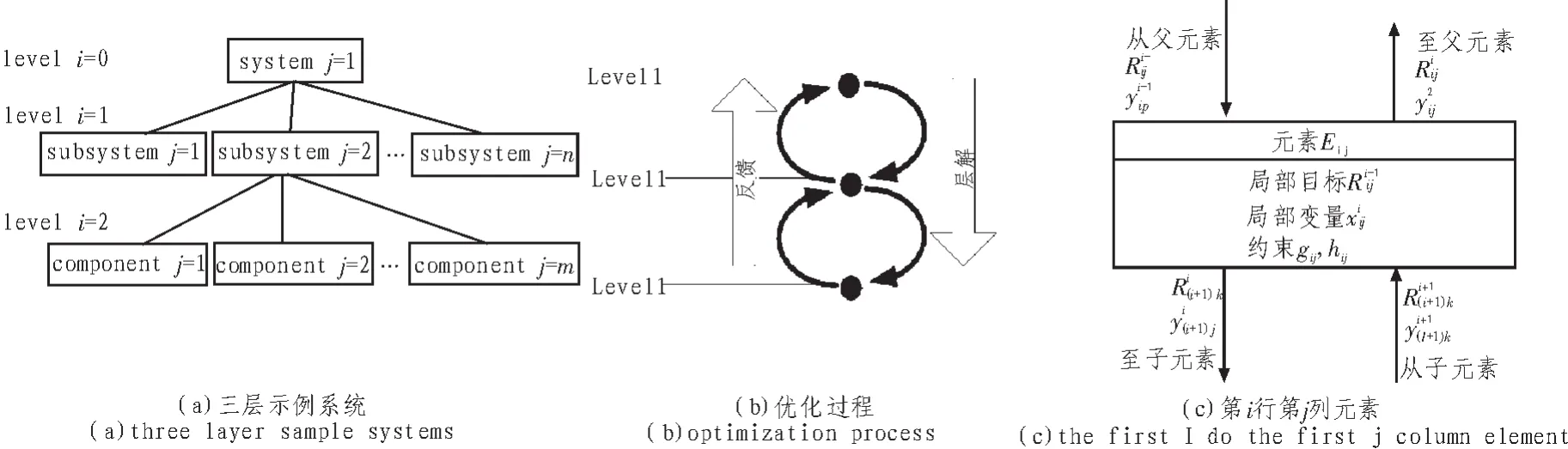
圖1 TC優化流程圖Fig.1 TC optimization flow chart

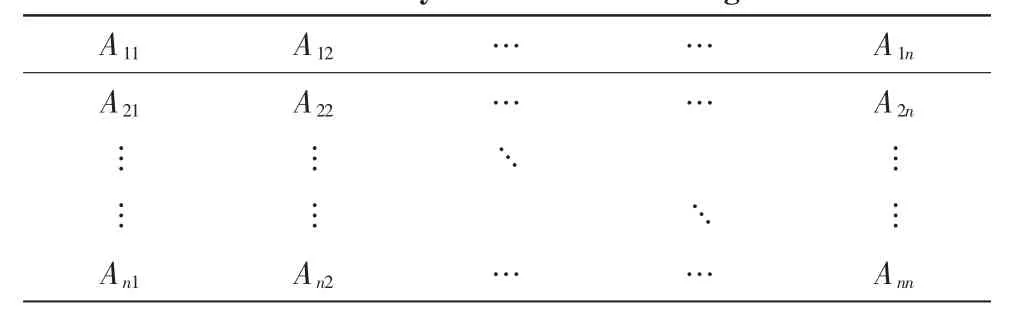
表1 二值DSM示意圖Tab.1 Binary DSM schematic diagram

如表1所示，在二值DSM中：

通過確定設計任務之間的信息聯系并根據DSM的定義可以得到一個只有0，1數字的初始化DSM。對角線上方的“1”表示下一環節設計任務反饋信息給上一環節設計任務，即逆序。對角線下方的“1”表示上一環節設計任務傳遞信息給下一環節，即順序。初始化的DSM通過DSM運算（重構、劃分、聚類等），實現任務重排、簡化、解耦或分解，以便系統求解。

3 基于DSM的ATC優化模型

雖然目標級聯（ATC）法是多層次非集中式的分解協調多學科優化方法，但如果分解不當就會造成任務間信息聯系過多，難以實現協同優化，同時產生過多的信息交互，增加ATC迭代次數。對此，首先利用DSM（包括改進和分層DSM）來描述由多個子系統（服務）組成的ATC復雜耦合關系和管理優化進程的任務順序（如圖2所示），通過DSM運算（如劃分、聚類等）對子系統及相互關系進行規劃和重組，實現任務重排、簡化、解耦、或分解，以便系統求解。

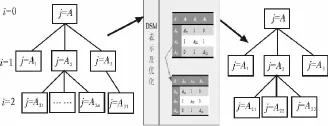
圖2 TC系統的DSM表示與規劃示意圖Fig.2 TC system DSM said and planning schematic diagram

4 實例分析

以齒輪減速器的設計優化為例。減速器設計優化的目標是在滿足齒的彎曲應力、接觸應力以及軸的扭轉變形、應力約束和齒輪幾何約束的條件下，使齒輪減速器的體積最小。

圖3為二級減速器的主要結構，首先利用DSM分析減速器內部零部件之間的相互聯系，找出設計主體及設計先后順序，然后運用目標級聯進行層次優化，以此達到優化目的。

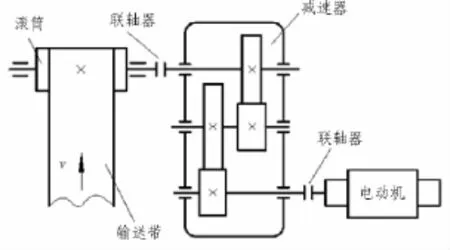
圖3 二級減速器主要結構Fig.3 Secondary reducer main structure

圖4是二級減速器各零部件相互間的信息聯系，建立其對應的初始DSM，如表2所示，按照DSM重構的基本原則，使DSM盡可能成為下三角矩陣，由此得到重構的DSM[5]，如表3所示。

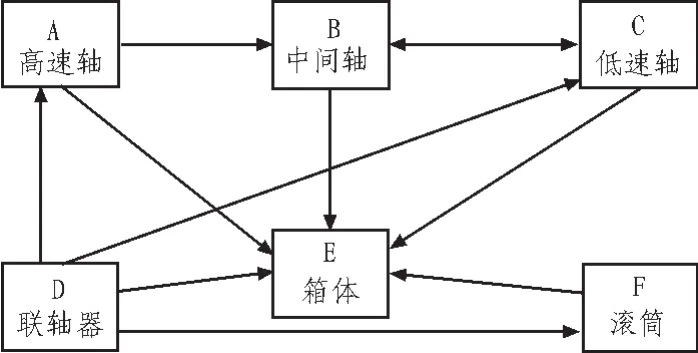
圖4 二級減速器各零部件之間的信息聯系Fig.4 Secondary reducer between components of information contact

由重構DSM可知，聯軸器D不需要其他零部件為其提供任何信息，因此聯軸器D最早設計完成。箱體E需要其他零部件為其提供設計信息，因此箱體E放在其他學科設計之后設計。高速軸A，中間軸B和低速軸C，他們相互耦合，設計C時既要考慮到A又要考慮到B，因此將A，B，C看成一個整體來設計執行。由此可以得出減速器的設計及加工的層次結構。

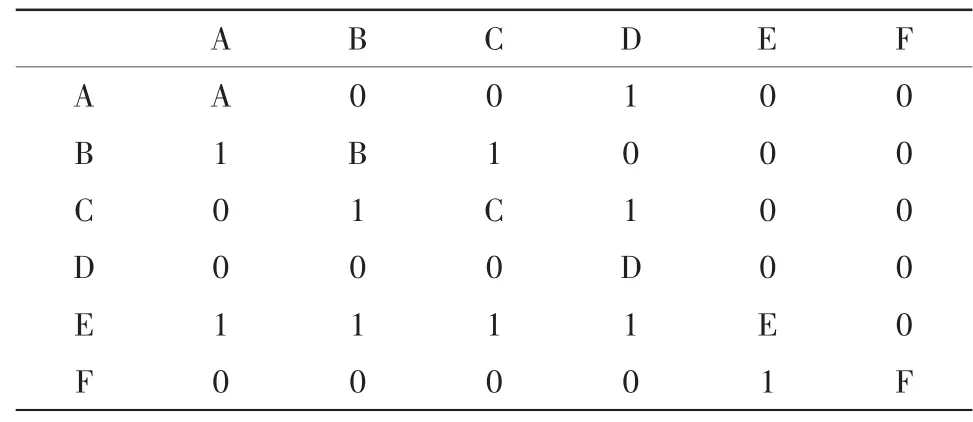
表2 初始DSMTab.2 Reconstruction DSM

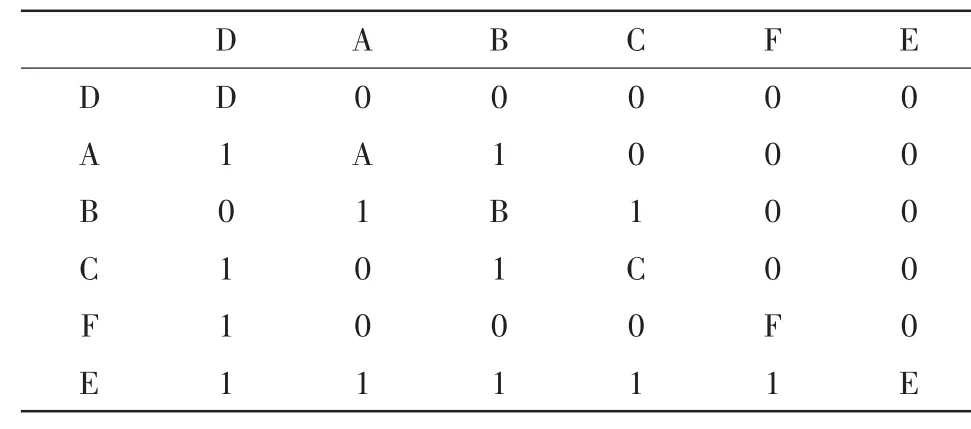
表3 重構DSMTab.3 Initial DSM

經過DSM重組從而理清各零部件的相互聯系，便于利用目標級聯法進行系統求解。從圖5中可以得知減速器設計主要是設計軸，只要使得高速軸、中間軸、低速軸以及齒輪之間結構最緊湊就會使整個減速器的體積最小，重量最輕。

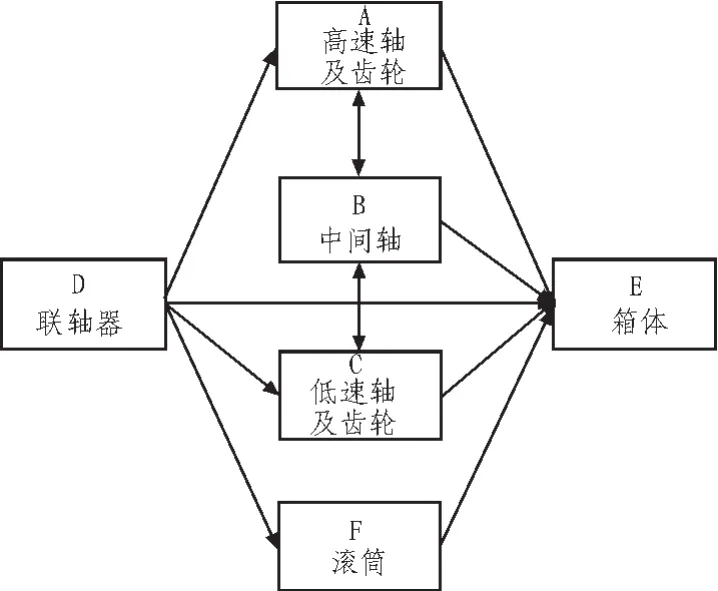
圖5 減速器設計及加工層次結構Fig.5 Reducer design and processing hierarchical structure

根據ATC的設計思想，將減速器的優化設計分為外觀層和內部層。外觀層的任務是設計箱體尺寸，使得整個減速器的外觀尺寸滿足要求。內部層的任務是設計高速軸、中間軸、低速軸及齒輪的尺寸，使得減速器整個內部結構緊湊。因此也可以看出外觀層和內部層的尺寸是相互影響的。

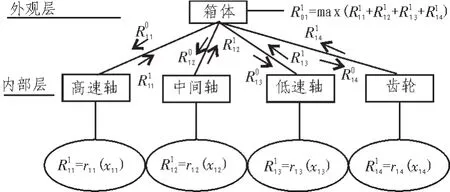
圖6 基于ATC的減速器設計優化模型Fig.6 Based on the ATC reducer design optimization model

圖6是基于ATC思想建立的減速器設計優化模型。其數學模型[6]為

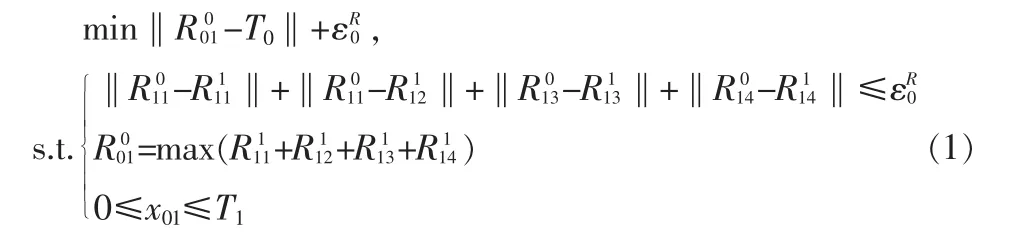
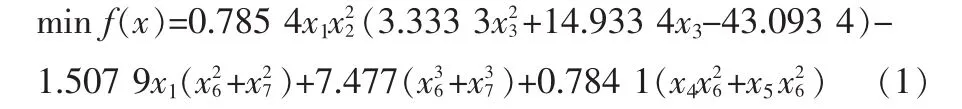
如果設定 T0=0.5，0≤===≤0.5，0≤===≤0.5，2.6≤x1≤3.6，0.7≤x2≤0.8，17≤x3≤28，7.3≤x4≤8.3，7.3≤x5≤8.3，2.9≤x6≤3.9，5.0≤x7≤5.5。 則可以得到優化結果，如表3所示。

表3 設計優化結果Tab.3 Result of design optimization

5 結束語

目標級聯法常常解決大規模多層次的系統優化，由于大規模混合層次系統通常復雜，直接利用目標級聯法很難理清層次關系和系統所需要解決重要問題。文中利用結構設計矩陣解決復雜耦合關系的優點，在應用目標級聯法解決問題之前利用結構設計矩陣運算減少信息交互，理清系統的復雜關系。然后以齒輪減速器的優化設計為例驗證，得出齒輪減速器的設計重點。

[1]張利強，王冰冰.多學科設計優化中目標層解分析法的研究[J].計算機仿真，2008，25（11）:195-199.ZHANG Li-jiang，WANG Bing-bing.Multidisciplinary design optimization of the target layer solution analysis[J].Computer simulation，2008，25（11）:195-199.

[2]唐敦兵.基于設計結構矩陣DSM的產品設計與開發[M].北京:科學出版社，2009.

[3]趙遷，陳瀟凱，林逸.改進的解析目標分流法[J].計算工程與設計，2010，31 （21）:4701-4703.ZHAO Qian，CHEN Xiao-kai，LIN Yi.The improved analytical target method[J].Calculation Engineering and Design，2010，31（21）:4701-4703.

[4]盛海濤，魏法杰.設計結構矩陣優化算法的研究與比較[J].計算機集成制造系統，2007，13（7）:1255-1260.CHENG Hai-tao，WEI Fa-jie.Theresearch and comparison about design structure matrix optimization algorithm[J].Computer integrated manufacturing systems，2007，13 （7）:1255-1260.

[5]常鋒娟，盧章平.設計結構矩陣在機械協同設計中應用[J].機械與電子，2001（4）:18-20.CHANG Feng-juan，LU Zhang-ping.The application of design structure matrix in the mechanical of collaborative design[J].Mechanical and electronic，2001（4）:18-20.

[6]黃英杰，姚錫凡，顏亮.基于目標級聯法和遺傳算法的多學科設計優化研究[J].機械設計與制造，2010（9）:39-41.HUANG Ying-jie，YAO Xi-fan，YAN Liang.The optimization study based on the target cascade method and genetic algorithm of multidisciplinary design[J].Mechanical design and manufacturing，2010（9）:39-41.