改進多種群遺傳算法在墻土系統損傷識別中的應用

劉禮標，張永興，陳建功

（重慶大學 土木工程學院；山地城鎮建設與新技術教育部重點實驗室，重慶400045）

結構系統損傷表現為結構動態特性的變化，將導致結構產生不同程度的安全隱患。土木工程設施（如高層住宅、大跨度橋梁、地鐵和支擋結構等）在現實中具有非常重要的地位，及時對結構進行損傷檢測可以減少很多安全事故的發生，準確識別出結構損傷位置和損傷程度是有必要的。在過去幾十年里許多結構損傷識別方法不斷地被提出，其中采用最優化方法識別結構損傷位置和程度被廣泛應用。

遺傳算法作為一種基于人工智能的優化算法，具有更強的全局搜索能力，在不同結構類型損傷診斷中的 應 用 很 廣 泛［1－14］。Chou 等［1］采 用 遺 傳 算 法對一桁架橋進行損傷識別；Perera等［2］結合特征方程、MTMAC指標構造的目標函數和遺傳算法對一簡支梁結構進行損傷定位；Koh等［3］基于綜合MDLAC指標的遺傳算法對結構多處損傷位置和損傷程度進行識別；Meruane等［5］基于模態特性和實數編碼的混合遺傳算法對三維空間桁架結構進行損傷識別；Nobahari等［6］基于綜合mDLAC指標和改進遺傳算法分別對懸臂梁結構和桁架結構進行損傷識別；Liu等［7］采用頻率改變率和MAC指標值構造多目標函數，基于遺傳算法優化求解對簡支梁結構進行損傷識別；袁穎等［8－9］提出了一種基于殘余力向量法和改進遺傳算法相結合的結構損傷識別方法，以節點的殘余力向量構造用于遺傳搜索優化的目標函數形式，利用改進的遺傳算法進行了噪聲條件下的結構損傷定位和定量研究；尹濤等［10］在傳統遺傳算法的變異算子里引入零變異率因子，使種群中時刻保持一定數量的零值元素，即相當于用結構的損傷只是發生在局部這個信息約束了傳統的遺傳算法，對框架結構進行損傷定位；陳存恩等［11］提出一種結合靈敏度修正的遺傳算法對一個4層平面框架結構進行損傷診斷等。然而，現有遺傳算法的大多數研究文獻都是針對簡單的梁結構、桁架結構、框架結構等。

針對板結構的墻土系統損傷識別研究相對較少，張永興等［15］對墻土系統模態特性進行分析，僅研究了損傷對模態特性的影響，但并未對損傷識別方法進行研究。為此，本文提出一種改進的多種群遺傳算法的墻土系統損傷識別方法，首先利用模態參數和物理參數關系，通過系統特征方程建立目標函數，再利用改進的多種群遺傳算法搜索得到系統的損傷位置和損傷程度。主要研究墻后土體存在不同程度損傷時的識別方法，對于擋墻本身存在損傷時，按本文思路也可對損傷位置和損傷程度進行識別。

1 基本模型

1.1 墻土系統簡化動測模型

本文旨在通過反映墻土系統模態特性的特征方程來識別墻土系統的損傷，建立了簡化動測模型，為便于分析作以下基本假定：1）懸臂擋墻底板的剛度較大，忽略底板的影響，將立板底部視作固接；2）懸臂擋墻視為薄板單元，離散后計算擋墻結構的質量矩陣、剛度矩陣、阻尼矩陣；3）土體簡化成附加剛度和附加阻尼來模擬，和擋墻附著在一起共同運動的墻后土體簡化成附加質量集中在節點處；4）擋墻與土體之間完全接觸，模型見圖1。

圖1 懸臂擋墻 巖土系統的簡化動測模型

文中主要基于墻土系統模態特性進行墻土系統損傷識別，一般情況下阻尼可以忽略不計，因此，圖1中土體附加阻尼系數csi取0。

1.2 墻土系統損傷動力特性模型

當墻后填土存在不同程度的損傷（如不密實、空洞等現象）時，假定損傷后土體附加剛度可以表示成無損傷狀態下土體附加剛度乘以反映損傷程度βi的系數αi，此時簡化模型中土體附加剛度可表示為：

式中：αi稱為附加剛度折減系數，其值介于［0，1］之間，對于無損傷單元，αi＝1。

土體發生損傷時的墻土系統特征方程為：

假設土體發生損傷僅降低附加剛度，而不考慮附加質量降低，并且土體發生損傷后仍滿足線性振動。若q對應無土體附加參數的自由度，r對應有附加土體參數自由度，則有：

上式可拆分為：

2 損傷識別的改進多種群遺傳算法

簡單遺傳算法容易出現早熟和停滯現象，為了克服簡單遺傳算法的缺點，提高全局搜索能力，本文提出應用改進多種群遺傳算法（IMGA）進行墻土系統損傷識別，主要對編碼方案、交叉算子和變異算子進行改進。IMGA主要思想是每個子種群分別獨立采用遺傳算法進行復制、交叉、變異操作，子種群每進化若干代就進行子種群間的遷移。

2.1 初始化種群

設計的初始種群長度為52，包含的變量分別為各測點對應的墻后土體附加剛度折減系數 （α1，α2，…，α52）。由于識別變量較多，為了提高算法性能，文中采用實數編碼方式，同時每個實數個體均能反映1個測點的損傷程度等優點。按照每個變量的范圍，隨機產生初始種群并分割成M個子種群。

2.2 適應值函數的確定及選擇操作

墻土系統損傷識別主要目的是識別出各點的附加剛度損傷程度。由于式（8）中不含反映土體損傷程度系數，因此，損傷程度識別問題的關鍵是如何根據式（9）識別出附加剛度折減系數αi。因此，利用最小二乘法準則，式（9）可轉化為求解如下非線性優化問題。

選擇f（α）為算法的適應值函數，然后根據非線性排序獨立計算各子種群中個體的適應度值。根據個體的適應度值按隨機遍歷抽樣進行選擇操作，從種群中選擇優良個體。

2.3 交叉、變異操作

簡單遺傳算法中交叉概率Pc和變異概率Pm是不變的，易造成較優個體破壞。因此，本文引入自適應交叉概率Pc和自適應變異概率Pm，其表達式分別如下：

式中：Pc1、Pc2、Pm1、Pm2為相應參數；fmax為種群中最大適應度值；為種群平均適應度值；f’為要交叉的兩個個體中較大的適應度值；f為要變異的個體適應度值。

交叉操作：由于采用實數編碼，按自適應交叉概率Pc執行算術交叉操作，按下式產生兩個新個體：

式中：r是［0，1］上的隨機數，t是當前代數。

變異操作：采用實數編碼時，變異算子變成一個主要的搜索算子，按照自適應變異概率Pm執行非均勻變異操作，按下式產生新個體：

式中：r、R是［0，1］上的隨機數，t是當前代數。

2.4 遷移操作

滿足遷移條件時，將子種群中最適應的20%（遷移率為0.2）的個體被選擇遷移，最鄰近的子種群在他們之間交換個體。

2.5 終止條件

循環執行2.2～2.4步的操作，直到目標函數minf（α）達到滿意值或達到最大迭代次數時，終止計算。這時輸出的變量即為識別損傷位置和損傷程度。損傷識別的改進多種群遺傳算法流程圖見圖2。

本文計算中改進的多種群遺傳算法的主要參數：子種群數量M＝5，子種群規模N＝40，變量個數Nvar＝52，交叉概率參數Pc1＝0.9、Pc2＝0.5，變異概率參數Pm1＝0.4、Pm2＝0.1，子種群遷移率rMIGR＝0.2，遺傳代數T＝5 000。

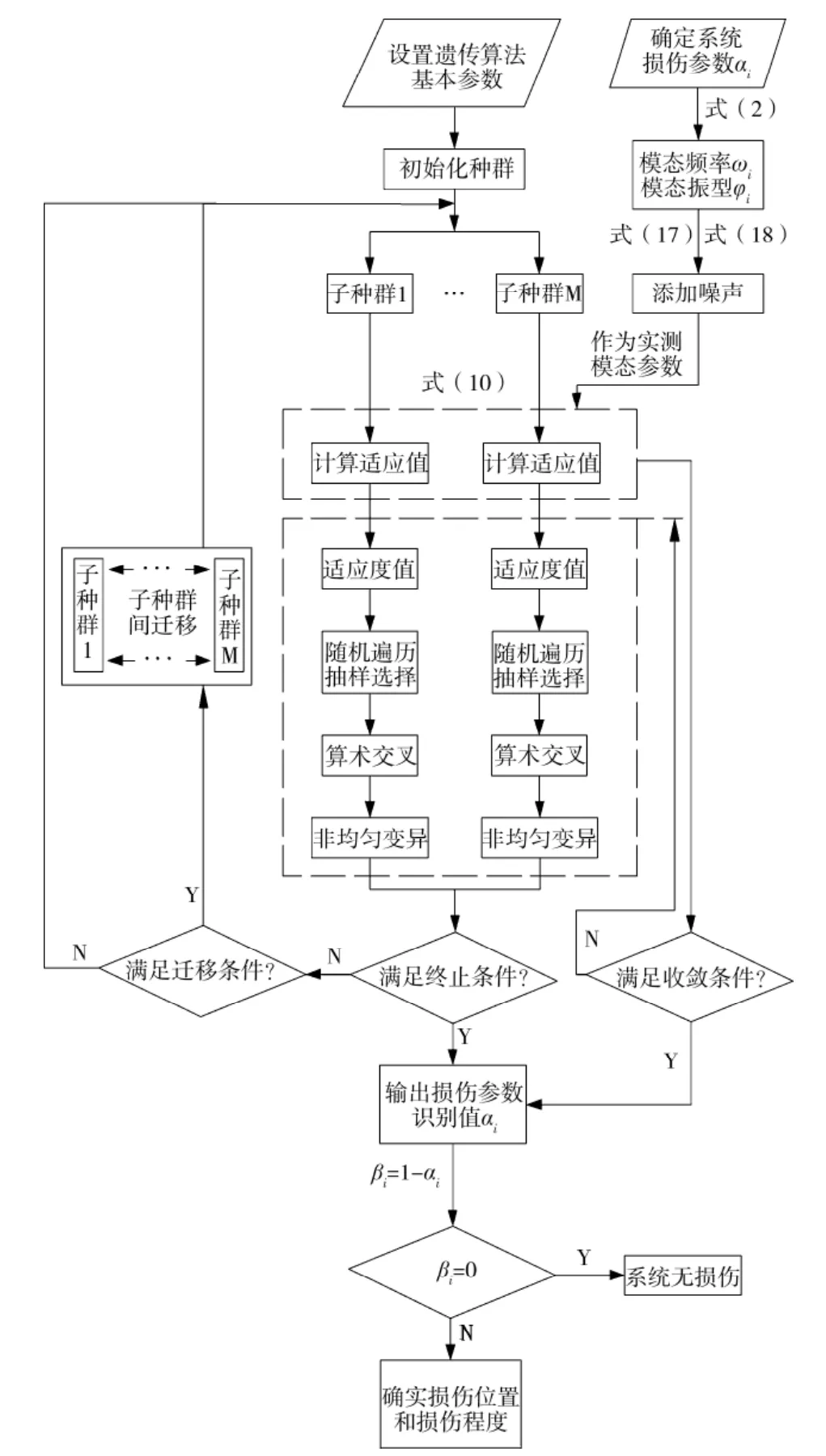
圖2 改進多種群遺傳算法流程圖

3 算例研究

研究算例基本參數：某懸臂擋墻彈性模量Ew＝28GPa，泊松比μw＝0.2，密度ρw＝2 450kg／m3，阻尼比ξw＝0.02；墻后填土彈性模量Es＝288MPa，泊松比μs＝0.3，密度ρs＝1 800kg／m3，阻尼比ξs＝0.05，粘聚力Cs＝3.8kPa，內摩擦角φs＝31°。墻土系統整體有限元模型尺寸見圖3，擋墻縱向長度方向取12m，測點布置圖見圖4。

3.1 研究方式

在有限元離散處理中，擋墻按圖3測點布置圖進行離散化，從左往右從下往上的單元編號用矩陣E表示，相應節點編號用矩陣N表示：

圖3 墻土系統整體模型尺寸示意圖（單位：mm）

圖4 測點布置圖

采用ANSYS對墻土系統無損狀態下的整體模型進行瞬態分析得到測點加速度響應曲線，識別到系統頻率和振型。為使問題簡化，假定無損狀態下基于模態參數的物理參數識別方法得到的土體附加參數是精確的，部分節點土體附加參數見表1。

表1 土體附加參數

假設墻后填土發生損傷時引起相鄰節點處附加剛度損傷程度是已知的，計算出墻土系統模態參數，同時為了驗證本文提出的墻土系統損傷識別方法的抗噪性能，按式（17）和（18）考慮隨機噪聲影響，然后將其作為式（10）的輸入數據分析噪聲對識別結果的影響。

式中：α和β分別表示頻率和振型的噪聲水平；R為［－1，1］上正態分布分布的隨機數。模擬的損傷工況見表2。

表2 損傷工況

由于對實際擋墻進行現場振動測量時受到多方面因素制約，不可能得到墻土系統所有的模態振型，一般只能獲得低階的模態振型，因此，本文分析中僅采用前三階模態振型φ1～φ3和前三階模態頻率ω1～ω3來識別墻后土體損傷位置和損傷程度。

對于土體附加剛度損傷程度識別準確性的評價用平均程度誤差表示，即：

式中：N為待識別參數個數；βI，i為識別得到的附加剛度損傷程度值；βA，i為附加剛度實際損傷程度值；MMEE值越小意味著損傷識別結果越準確。

3.2 損傷識別結果分析

分別對4種工況進行損傷識別，損傷識別結果分別見圖5～8，圖中x軸為擋墻高度方向，y軸為擋墻縱向長度方向。

由圖5～8分析可知：在無噪聲狀態下，無論對單處損傷還是多處損傷、單一損傷程度還是多損傷程度，都能夠精確的識別出土體損傷程度；對模態參數添加噪聲后，本文方法識別的精度比無噪聲狀態下識別精度低，但仍然能夠比較準確的識別出相應的損傷位置和損傷程度；根據不同工況的MMEE值，可以得到噪聲對損傷識別有一定的影響，且隨著損傷數量的增加MMEE值也增加，即損傷識別精度逐漸下降，因此，為了提高識別結果的精度，對現場測試數據處理時要注意消除噪聲。

圖5 工況1損傷識別結果

圖6 工況2損傷識別結果

圖7 工況3損傷識別結果

圖8 工況4損傷識別結果

3.3 算法性能的比較

為了便于比較改進多種群遺傳算法和簡單遺傳算法計算性能的優越性，使IMGA和GA的初始種群保持一致，其他參數均相同。以工況2為例，同時不考慮測試噪聲的影響。運行結果見圖9。

圖9 算法性能比較圖

由圖9可知，改進多種群遺傳算法收斂速度更快，在2 000代基本收斂到了近優解，迭代到5 000代時，MMEE值降低到了0.564%，得到了比較滿意的結果；簡單遺傳算法在迭代到5 000代時，仍未收斂到較為理想的結果，因此，采用改進多種群遺傳算法的尋優能力強于簡單遺傳算法。

4 結 論

本文基于墻土系統特征方程構造損傷識別的目標函數，結合改進的多種群遺傳算法進行最優化計算來識別墻土系統的損傷，得到以下結論：

1）文中改進的多種群遺傳算法能有效的同時識別出墻土系統的損傷位置和損傷程度，彌補了現有的損傷識別方法中需要先識別出損傷位置，再進一步判定損傷程度的缺點。

2）無論對單處損傷還是多處損傷、單一損傷程度還是多損傷程度，按本文識別方法都能較好的識別出墻土系統的損傷位置和損傷程度。

3）為了驗證本文識別方法的抗噪性能，對理論模態參數引入隨機噪聲的影響，采用改進的多種群遺傳算法的損傷識別方法同樣具有較好的識別效果，具有較強的抗噪聲能力。

［1］Chou J H，Ghaboussi J.Genetic algorithm in structural damagEdetection ［J］.Computers and Structures，2001，79：1335－>1353.

［2］Perera R，Torres R.Structural damagEdetection viamodal data with genetic algorithms ［J］.Journal of Structural Engineering，2006，132（9）：1491－>1501.

［3］Koh B H，DykES J.Structural healthmonitoring for flexiblEbridgEstructures using correlation and sensitivity ofmodal data［J］.Computers ＆Structures，2007，85：117－>130.

［4］HEX，Kawatanim，Hayashikawa T，et al.A bridgEdamagEdetection approach using train－>bridgEinteraction analysis and GA optimization［J］.Procedia Engineering，2011，14：769－>776.

［5］MeruanEV，Heylen W.An hybrid real genetic algorithm to detect structural damagEusingmodal properties ［J］.Mechanical Systems and Signal Processing，2011，25：1559－>1573.

［6］Nobaharim，Seyedpoor Sm.Structural damagEdetection using an efficient correlation－>based index and amodified genetic algorithm ［J］.mathematical and Computermodeling，2011，53：1798－>1809.

［7］Liu H，Xin kG，Qi Q Q.Study of structural damagEdetection withmulti－>objectivEfunction genetic algorithms［J］.Procedia Engineering，2011，12：80－>86.

［8］袁穎，林皋，閆東明，等.基于殘余力向量法和改進遺傳算法的結構損傷識別研究［J］.計算力學學報，2007，24（2）：224－>230.Yuan Y，Lin G，Yan Dm，et al.Study on structural damagEidentification based on residual forcemethod and improved genetic algorithm ［J］.ChinesEJournal of Computationalmechanics，2007，24（2）：224－>230.

［9］袁穎，林皋，閆東明，等.基于改進遺傳算法的橋梁結構損傷識別應用研究［J］.應用力學學報，2007，24（2）：186－>190.Yuan Y，Lin G，Yan Dm，et al.Improved genetic algorithm for bridgEdamagEdetection ［J］.ChinesEJournal of Appliedmechanics，2007，24（2）：186－>190.

［10］尹濤，朱宏平，余嶺.運用改進的遺傳算法進行框架結構損傷檢測［J］.振動工程學報，2006，19（4）：525－>531.Yin T，Zhu H P，Yu L.Application study of an improved genetic algorithm for framEstructurEdamagEdetection［J］.Journal of Vibration Engineering，2006，19（4）：525－>531.

［11］陳存恩，李文雄.結合靈敏度修正的遺傳算法的結構損傷診斷［J］.地震工程與工程振動，2006，26（5）：172－>176.Chen C E，Li W X.Structural damagEdiagnosis by genetic algorithm with sensitivity updating ［J］.EarthquakEEngineering and Engineering Vibration，2006，26（5）：172－>176.

［12］尹強，周麗.基于遺傳優化最小二乘算法的結構損傷識別［J］.振動與沖擊，2010，29（8）：155－>159.Yin Q，Zhou L.Structural damagEidentification based on GA optim ized least squarEestimation［J］.Journal of Vibration and Shock，2010，29（8）：155－>159.

［13］李小平，鄭世杰.基于遺傳算法和拓撲優化的結構多孔洞損傷識別［J］.振動與沖擊，2011，30（7）：201－>204.Li X P，Zheng S J.Multi－>holEdamagEdetection in structures based on genetic algorithms and topology optimization［J］.Journal of Vibration and Shock，2011，30（7）：201－>204.

［14］黃天立，樓夢麟，任偉新.基于CMDLAC指標和遺傳算法的結構損傷定位研究［J］.計算力學學報，2009，26（4）：529－>534.Huang T L，Loum L，Ren W X.Structural damagElocalization based on thecmDLAC and genetic algorithm［J］.ChinesEJournal of Computationalmechanics，2009，26（4）：529－>534.

［15］張永興，劉世安，陳建功.土體對懸臂擋墻模態的影響與應用［J］.土木建筑與環境工程，2009，31（3）：72－>77.Zhang Y X，Liu S A，Chen J G.InfluencEand its application of soil on themodEof cantilever retaining wall［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2009，31（3）：72－>77.