無約束優化問題的差分進化算法求解

洪云飛 （長江大學期刊社；信息與數學學院，湖北 荊州434023）

陳 忠 （長江大學信息與數學學院，湖北 荊州434023）

差分進化算法 （Differential Evolution，DE）是一種基于群體差異的啟發式隨機搜索算法［1］。差分進化算法具有全局優化性能好，結構簡單和易于實現的特點，在函數優化［2－3］、多目標優化［4］、背包問題［5－6］、系統辨識［7－8］等方面得到廣泛應用。下面，筆者利用差分進化算法求解無約束優化問題。

1 約束優化問題的數學描述

不失一般性，以最小化問題為例，無約束優化問題可描述為：

其中，S＝ ｛x∈Rn｜li≤xi≤ui，i＝1，2，…，n｝為問題的可行域。

2 差分進化算法的構成要素

1）編碼方法 使用差分進化算法求解一個問題之前，需要選擇一種編碼方法。編碼就是將實際問題的解用一種便于算法操作的形式來描述。根據問題的具體情況，可以靈活選擇編碼方式。如對于排序問題可采取順序編碼，對于背包問題可以采取0－1編碼。對于實優化問題，一般可以直接使用實數編碼，編碼的每一位就是解的相應維的取值。筆者選擇實數編碼作為算法實現的編碼方式。

2）適應度函數的構造 類似于遺傳算法，差分進化算法的適應度函數也是用來對搜索狀態進行評價的。一般情況下，將目標函數作為適應度函數是最直接也是最容易理解的做法。當然，對目標函數的任何變形都可以作為適應度函數，只要這個變形是嚴格單調的。筆者直接把目標函數作為適應度函數。

3）種群規模 種群規模NP是一個整型參數。當NP很小的時候，由于無法保證種群的多樣性，算法容易陷入局部最優解。然而，種群規模過大將導致計算時間大幅增加，降低算法的執行效率。并且當種群規模增長到一定水平時，繼續增加種群規模將不再有顯著作用。因此，針對不同的具體問題，需要設置合適的種群規模算法才能達到較好的搜索性能。

4）初始解的獲得 差分進化算法可以隨機給出初始解，也可以事先使用其他算法給出一個較好的初始解。由于差分進化算法主要是基于個體之間的差異推動群體進化，因此初始解的好壞對算法的搜索性能有較大影響。尤其是一些帶有復雜約束的優化問題，隨機給出的初始解很可能是不可行的，甚至通過多步搜索也很難找到一個可行解，這個時候應該針對特定的復雜約束，采用啟發式方法或其他方法找到可行解作為初始解。筆者以標準測試函數檢測算法性能時采用隨機方式生成初始解。

5）進化操作 差分進化算法的基本進化操作包括變異、交叉和選擇。算法在優化迭代過程中，采用規模為NP的D維向量（i＝1，2，…，NP）作為第g代的種群，在搜索空間中進行尋優，其中NP為種群規模，D為解空間維數。

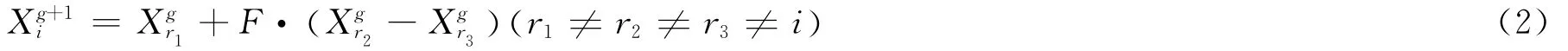
式中，CR為交叉概率，范圍在0～1之間；rand（）為0～1范圍內生成的隨機數；jrand為1～D之間隨機選取的整數隨機量。

式中，f（·）為適應度函數。

6）停止準則 一般使用最大迭代次數或可以接受的滿意解作為停止準則。筆者選擇最大迭代次數作為算法停止的控制參數。

3 差分進化算法步驟和流程

差分進化算法執行的步驟如下：

Step1 初始化。根據具體問題初始化種群。

Step2 判斷是否滿足停止條件。如果滿足，輸出結果，算法停止；否則繼續一下步驟。

Step3 執行變異操作。從父代群體中隨機選取3個個體，按照式 （2）執行變異操作，得到變異個體；

Step4 執行交叉操作。對變異個體按式 （3）執行交叉操作，得到交叉個體；

Step5 執行選擇操作。計算交叉個體的適應值，并與原個體進行比較，依據貪婪選擇原則執行選擇操作，返回Step2；

差分進化算法的執行流程如圖1所示。

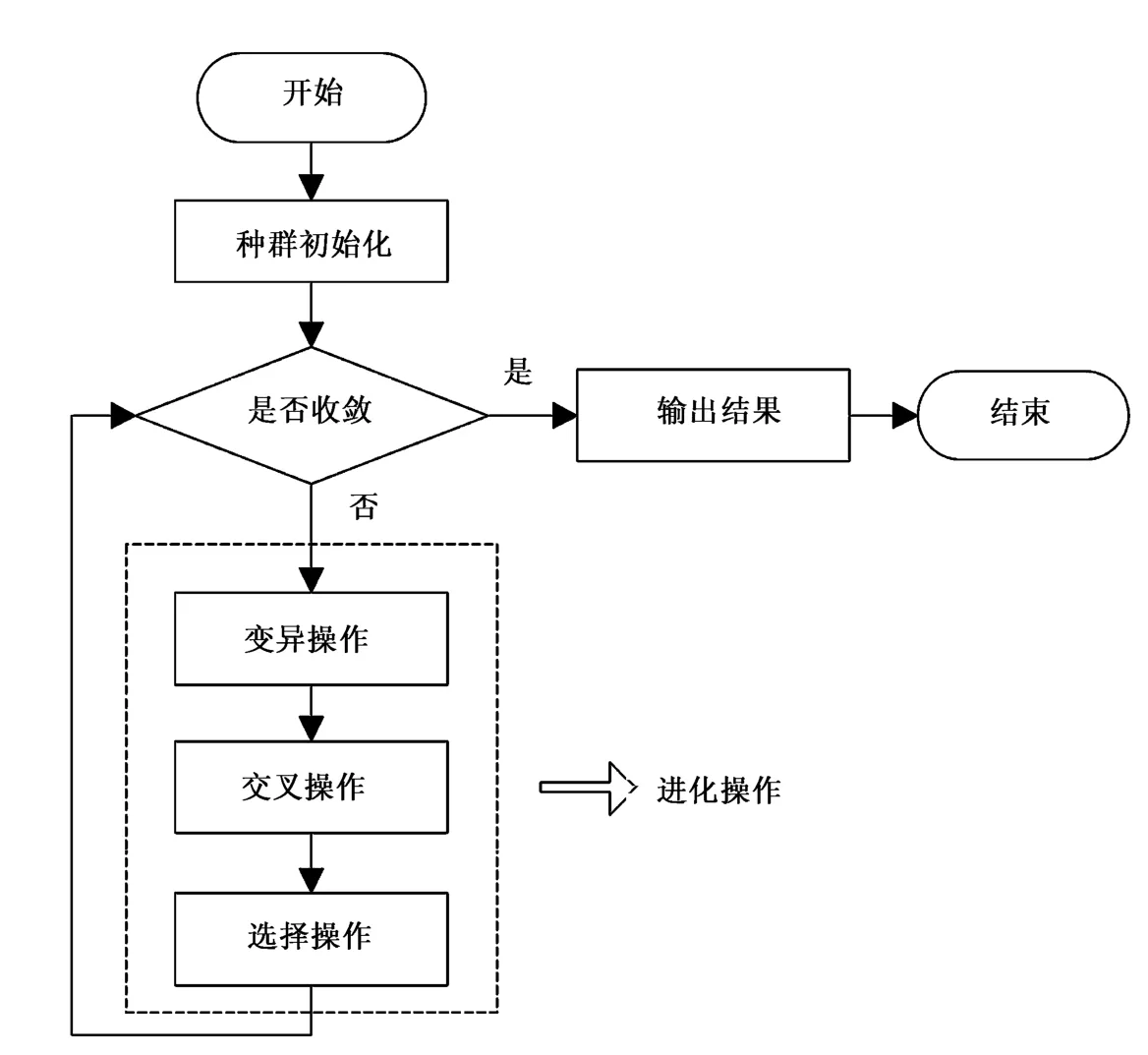
圖1 差分進化算法流程

4 數值試驗

通過標準測試函數來分析差分進化算法在求解數值優化問題時的尋優性能。筆者選取的標準測試函數如下：

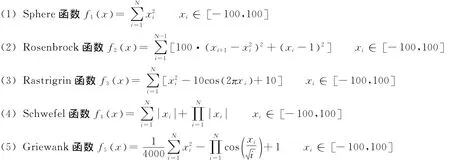
對于待求解問題本身來說，問題維度是影響計算規模的關鍵因素。對于求解算法而言，控制參數是影響算法性能的關鍵因素。在差分進化算法中，有3個主要控制參數：種群規模NP、變異操作中差分向量的縮放因子F以及交叉操作中的交叉因子CR。因此，筆者首先通過上述標準測試函數對差分進化算法的計算性能進行初步檢驗，同時分析不同控制參數對差分進化算法計算性能的影響，從而獲取比較合適的控制參數設置范圍，并以此為基礎展開后續并行差分進化算法的研究和測試工作。

較大的種群規模，一方面可以容納更多的不同個體，為種群多樣性提供了可能；另一方面增加了需要進行評價計算的個體數量，也就意味著算法尋優的時間必然要增加。因此，不能簡單地說種群規模的變化對算法求解性能影響的利弊，而需要進行大量模擬計算，把種群規模控制在一個合理的范圍內，既保證差分進化算法有足夠的特征各異的進化個體，又兼顧算法的求解耗時。

將問題維度固定為30，迭代次數為1000，縮放因子F固定為0.6，交叉因子CR固定為0.8，在不同種群規模情況下以差分進化算法對上述5個標準測試函數進行模擬計算，模擬計算結果如表1所示。

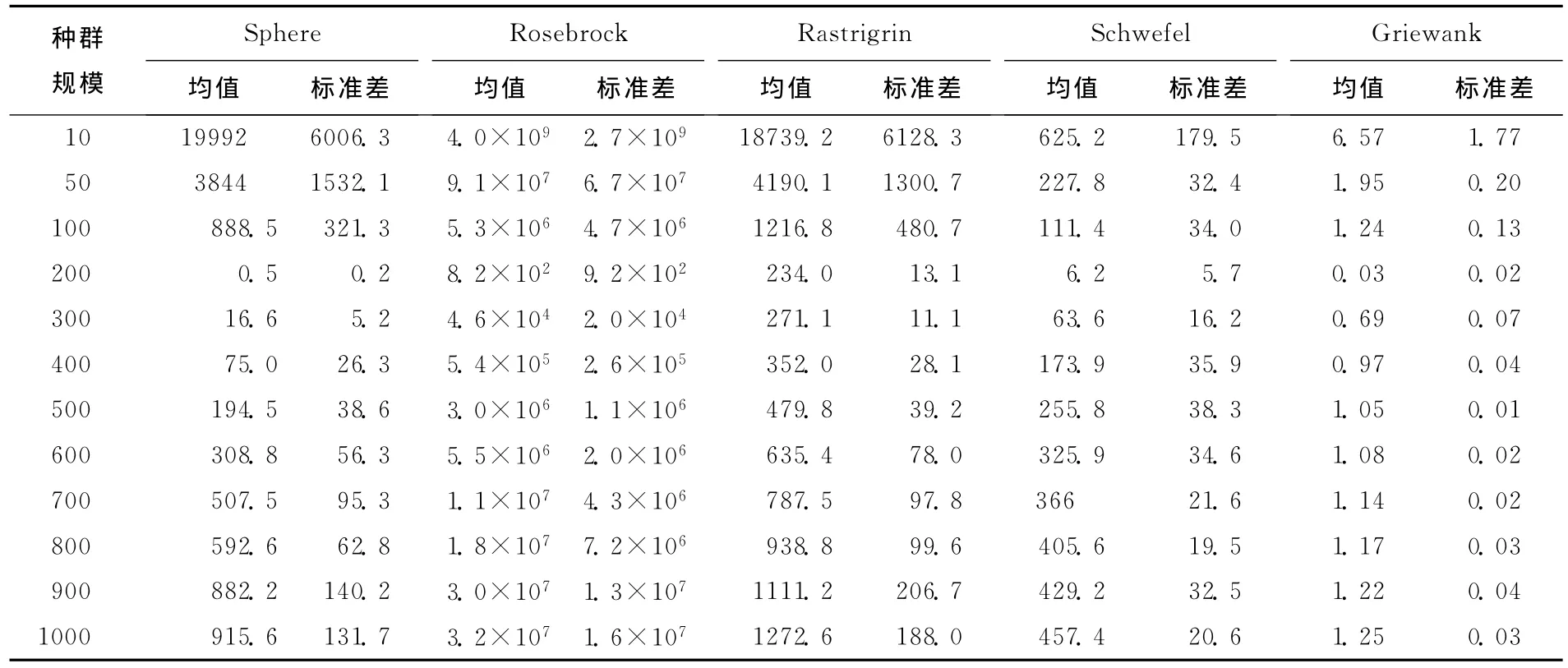
表1 不同種群規模下測試函數的模擬計算結果

由表1可見，當問題維度為30時，隨著種群規模的增加，差分進化算法尋優得到的結果逐漸向全局最優點靠近，但是當種群規模超過200左右時，算法的尋優結果并沒有繼續呈現較強的向全局最優點逼近的趨勢，反而呈現出一種震蕩或回退的趨勢，如圖2所示。該現象說明，在問題維度一定的情況下，種群規模超過某個閾值后，繼續增加種群規模未必能夠帶來尋優性能的增加。但是可以預見的是，其計算耗時必然會隨著種群規模的擴大而迅速增加。

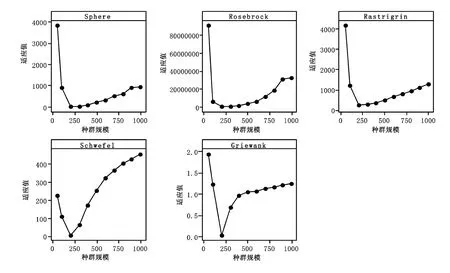
圖2 適應值與種群規模的關系

［1］Storn R，Price K.Differential evolution－A simple heuristic for global optimization over continuous spaces ［J］.Journal of Global Optimization，1997，11 （4）：341－359.

［2］Ali M M.Differential evolution with preferential crossover ［J］.European Journal of Operations Research，2007，181 （3）：1137－1147.

［3］Noman N，Iba H.Accelerating differential evolution using an adaptive local search ［J］.IEEE Trans on Evolutionary Computation，2008，12 （1）：107－125.

［4］Iorio A W，Li X D.Solving rotated multi－objective optimization problems using differential evolution ［A］.Proceeding of the 17th Australian joint conference on advances in artificial intelligence ［C］.Cairns，Australia，2004：861－872.

［5］Chen Peng，Li Jian，Liu Zhiming.Solving 0－1knapsack problems by a discrete binary version of differential Evolution ［A］.Proceeding of the 2nd International Symposium on Intelligent Information Technology Application ［C］.Shanghai，China，2008，II：513－516.

［5］Wang Ling，Fu Xiping，Mao Yunfei，et al.A novel modified binary differential evolution algorithm and its applications ［J］.Neuron computing，2012，98 （5）：55－75.

［7］Peng Bo，Liu Bo，Zhang Fuyi，et al.differential evolution algorithm based parameter estimation for chaotic systems［J］.Chaos，Solutions and Fractals，2009，39 （5）：2110－2118.

［8］Zhang Rui，Song Shiji，Wu Cheng.A hybrid differential evolution algorithm for job shop scheduling problems with expected total tardiness criterion ［J］.Applied Soft Computing，2013，13 （3）：1448－1458.