一種結合圖像增強的高斯噪聲組合濾波算法

余光華

(湛江師范學院信息與教育技術中心，廣東 湛江 524048)

責任編輯:時 雯

數(shù)字圖像在獲取過程以及后續(xù)的存儲、傳輸?shù)拳h(huán)節(jié)中，不可避免地受到噪聲的干擾。為了對數(shù)字圖像進行更好的研究和應用，有必要對圖像中的噪聲加以抑制，以最大限度恢復圖像中的目標細節(jié)信息，提高圖像的清晰度。干擾圖像的噪聲種類繁多，主要有高斯噪聲、脈沖噪聲、瑞利噪聲、泊松噪聲等，但其中的高斯噪聲和脈沖噪聲則較為常見。高斯噪聲包括電子電路產(chǎn)生的噪聲或是由于在照明度低、溫度高情形下圖像傳感器生成的噪聲;來源于圖像傳感器、傳輸信道、解碼過程中產(chǎn)生的黑白點噪聲則稱之為脈沖噪聲，當該類噪聲處于飽和狀態(tài)時，即為椒鹽噪聲。高斯噪聲密度大、噪聲強度的波動范圍較寬，圖像受該類噪聲的干擾程度不僅會隨著灰度級的不同而有所差異，并且在同一灰度級上也不盡一致，相對于椒鹽噪聲難以濾除［1］。

抑制圖像中的噪聲大體上有兩類方法:一類是基于圖像增強技術的方法，該類方法只需針對圖像感興趣區(qū)域采用圖像增強方法對圖像灰度動態(tài)范圍加以改善，從而提高圖像的視覺效果;另一類是濾波方法，即對圖像采用各類濾波方法對噪聲加以排除。目前學術界對濾波方法研究主要有以下幾個方向:1)單一濾波器及其改進算法，如中值濾波，在此基礎上發(fā)展而來的加權中值濾波［2］、多級中值濾波［3］、開關中值濾波［4］、極值中值濾波［5］等算法;2)具有嚴密的數(shù)學理論基礎的濾波方法，如形態(tài)學濾波［6］、小波去噪［7］、偏微分方程去噪［8］等;3)組合濾波方法，即充分發(fā)揮各類濾波算法的優(yōu)勢，取長補短對圖像噪聲進行有效濾除，如文獻［9－11］。單一濾波算法盡管得到一些改進，在濾波性能上得到一定程度的提升，但不免增加了計算復雜度，并且每一類算法在提升到一定程度時也難以再有所突破。組合濾波方法相對來說則較為靈活，可針對圖像噪聲，對各類濾波方法加以有機結合，不但提高了計算效率，濾波效果也較為理想，因此，該類濾波方法具有較好的研究和應用前景。

針對中值濾波對高斯噪聲基本無能為力的缺陷，本文嘗試對其進行改進，用于圖像高斯噪聲的抑制處理。將改進中值濾波器與小波域均值濾波器有機結合實現(xiàn)對高斯噪聲的逐次濾波。在此基礎上，結合圖像增強技術，提出了一種具有增強效果的高斯噪聲組合濾波算法。

1 本文算法基本流程

1.1 改進中值濾波算法

中值濾波(Median Filter，MF)是一類基于統(tǒng)計排序理論的非線性濾波方法，通過設計一定大小的窗口(濾波模板)在圖像中滑動，對圖像中某點在窗口中涉及到的所有像素點的灰度值進行排序，取其中間值作為該點的灰度值。因此，能否根據(jù)噪聲的強度和類型設計合適的濾波模板則成為制約中值濾波處理效果的關鍵因素。一般來說，模板過大對噪聲的濾波效果較為理想，但對于圖像邊緣等細節(jié)信息的模糊也是不可避免的;模板過小盡管不會不顯現(xiàn)模糊圖像細節(jié)信息，但無法盡可能排除噪聲的干擾。近年來，學者們針對中值濾波的濾波模板也進行了一系列改進，如加權中值濾波［2］通過對濾波模板中各灰度值賦予一定的權值，進行適當?shù)臄U展從而改變模板大小。此外，多級中值濾波［3］對噪聲圖像進行多尺度逐級中值濾波以盡可能濾除噪聲，同時避免圖像出現(xiàn)模糊。

鑒于不同大小的濾波模板具有不同的性能，以及受多級中值濾波思想的啟發(fā)，從濾波模板的角度，對經(jīng)典中值濾波進行適當改進，對圖像高斯噪聲進行多角度、多尺度、逐級中值濾波。改進中值濾波方法的基本步驟是:1)分別設計出尺度為3和5的水平和垂直方向的兩類一維模板，實現(xiàn)這兩個方向的逐級濾波，濾波模板如圖1所示;2)經(jīng)過上述處理后，水平和垂直方向噪聲基本濾除，但對角線方向噪聲仍存在，并且相對于整幅圖像而言，更為孤立，可采用二維3×3濾波進行處理，改進中值濾波基本思路如圖2所示。

1.2 小波域均值濾波

與MF類似，均值濾波(AF)也是一類基于模板操作的濾波方法，通過對圖像中某一像素點一定大小窗口內的所有像素取平均值作為該點的輸出值，從而實現(xiàn)對噪聲的抑制，是一種經(jīng)典的空間域線性濾波方法。當圖像中混有加性噪聲特別是高斯噪聲時，采用AF可快速排除噪聲干擾，但對于高強度的噪聲，也會導致影像出現(xiàn)不同程度的失真。小波變換能夠對圖像進行多分度的分解，可以獲得高頻和低頻兩類子帶圖像。并且該兩類圖像所含信息是不同的，低頻圖像包含原始圖像絕大部分信息，而高頻圖像則是原始圖像高頻信息的反映，相對來說，信息量較少。

在1.1節(jié)的步驟中，對噪聲圖像進行改進MF處理，可濾除一大部分噪聲，對于混有殘余噪聲圖像，如果僅進行空間域均值濾波處理，則濾波效果也不太理想。小波變換對信號能量具有“集中”的特性，即噪聲信號基本集中于高頻子圖像中，而低頻子圖像基本不受噪聲的干擾。盡管各高頻子圖像中，高頻信息特別是噪聲集中于特定方向分布，但總體來說，噪聲基本處于孤立狀態(tài)，因而可對殘余噪聲圖像進行小波域均值濾波，可獲得較好的濾波效果。

根據(jù)以上分析，本文對經(jīng)1.1節(jié)處理后的圖像進行小波域均值濾波處理。具體步驟為:1)對殘余噪聲圖像進行二維多尺度分解(尺度為3，小波基函數(shù)為“sym8”)，獲得低頻子圖像LL，水平方向高頻子圖像LH，垂直方向高頻子圖像HL以及對角線方向高頻子圖像HH;2)低頻子圖像LL不作處理，對于高頻子圖像(LH，HL，HH)分別進行模板為二維3×3和5×5的多尺度逐級均值濾波處理，獲得濾波后的高頻子圖像(LH'，HL'，HH');3)將高頻子圖像(LH'，HL'，HH')與低頻子圖像LL進行小波重構。

1.3 小波域增強函數(shù)設計

對圖像進行灰度拉伸，實現(xiàn)圖像動態(tài)范圍有效改善，以盡可能突出圖像感興趣目標信息的處理方法稱之為圖像增強。圖像增強技術大體上有兩類:一類是對圖像按照一定的函數(shù)進行灰度變換，按照函數(shù)的類型，該類方法可分為非線性變換、線性以及在此基礎上發(fā)展的分段線性變換等;另一類是對反映圖像灰度分布的直方圖進行諸如直方圖規(guī)定化、直方圖均衡化等處理以實現(xiàn)影像增強。圖像經(jīng)過上述處理后，盡管能夠取得一定的增強效果，但由于上述方法是對整幅圖像采用單個方法進行增強，圖像感興趣目標信息無法有效突出，并且在圖像含有少量噪聲情形下，上述方法無法在突出圖像信息的同時對噪聲進行有效抑制。

噪聲圖像先后經(jīng)過1.1節(jié)和1.2節(jié)的濾波后，噪聲基本得到濾除，但為了獲得灰度動態(tài)范圍較好的圖像，有必要對其進行增強處理。本文受分段線性變換增強方法的啟發(fā)，將線性變換與非線性變換方法引入到小波域中，提出了一種新型小波域增強函數(shù)模型。該函數(shù)模型可表示為

綜上所述，本文濾波方法主要由3部分構成:1)對噪聲圖像進行改進MF，以排除一部分噪聲的干擾;2)對改進MF后的殘余噪聲圖像進行小波域多級均值濾波處理，基本濾除圖像噪聲;3)對上述濾波后的圖像進行小波域增強處理，以改善圖像灰度分布，提高視覺效果。

2 實驗與分析

2.1 實驗結果評價方法

對于濾波后圖像質量的評價，目前大體上有主觀和客觀兩類方法。主觀方法主要是人對圖像質量進行主觀判斷，如主觀評分法(MOS)、平均主觀分數(shù)差異法(DMOS)等，但該類方法評價效果受到評價者的專業(yè)水平和數(shù)量等因素的限制;客觀方法主要是采用計算濾波后圖像的一些數(shù)值指標來實現(xiàn)對圖像質量的評價，代表性的有PSNR和MSE等。近年來基于人眼視覺系統(tǒng)(HVS)［12］的評價方法，如結構相似度(SSIM)［13］法得到了一定發(fā)展，理論上評價效果優(yōu)于PSNR和MSE。但由于PSNR和MSE等指標易于編程實現(xiàn)，且計算效率高，數(shù)值大小能基本反映出圖像質量優(yōu)劣等特性，仍是主流的評價方法。因此，本文對濾波后圖像質量進行主觀分析的同時，采用PSNR和MSE指標對其進行客觀評價。

2.2 實驗結果與分析

2.2.1 改進中值濾波性能測試

為了測試該類改進中值濾波對于高斯噪聲的抑制效果，對一幅灰度級為256，大小為512×512的“l(fā)ena.bmp”圖像，加入均值為0、不同方差的高斯白噪聲進行測試。定義PSNR值對測試結果進行定量評價，實驗結果如圖3和表1所示。

對圖3和表1數(shù)據(jù)進行分析可知，圖3e清晰度優(yōu)于圖3c和圖3d，并且在邊緣細節(jié)保持方面相對于前兩幅圖像而言也有一定優(yōu)勢。這體現(xiàn)在表1中，但高斯白噪聲方差為0.03時，改進MF優(yōu)于AM達3～4 dB左右，并且當噪聲處于0.09時，改進MF的PSNR值仍高于AM。這可充分表明，改進AM方法，對于圖像高斯白噪聲的濾波具有較好的效果。

圖3 改進中值濾波性能測試

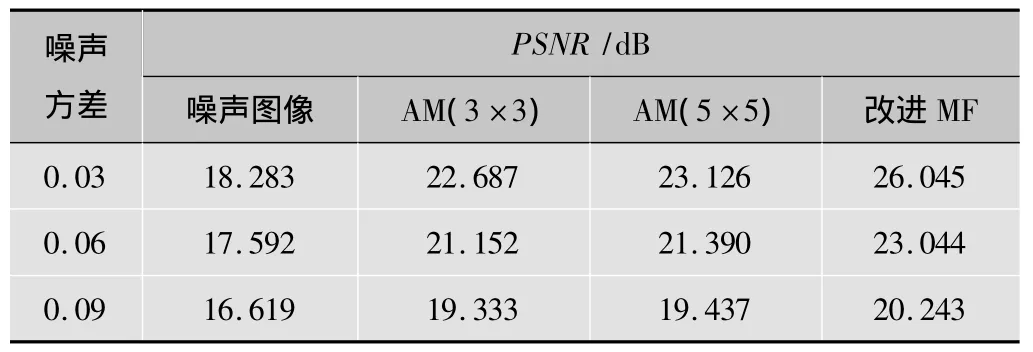
表1 改進中值濾波器PSNR

2.2.2 本文濾波算法性能測試

為了測試本文濾波方法的性能，在MATLAB7.0環(huán)境下，編寫相關程序對圖3a所示的大小為512×512、灰度為256級的“l(fā)ena.bmp”圖像進行濾波實驗。通過對該測試圖像加入均值為0、不同強度的高斯白噪聲，并與文獻［1］和文獻［9］進行性能比較。實驗結果如圖4和表2、表3所示;本文濾波方法中，小波域增強函數(shù)系數(shù)在不同高斯白噪聲強度下的取值，如表4所示。

圖4 幾種濾波方法試驗結果

表2 幾種濾波方法的PSNR

表3 幾種濾波方法的MSE

表4 不同噪聲強度下小波域增強函數(shù)系數(shù)取值

對試驗結果進行分析如下:

1)濾波實驗結果分析

(1)主觀分析:噪聲圖像經(jīng)過文獻［1］和文獻［9］濾波后，圖像信息集中于較大的灰度級上，表現(xiàn)為圖像較為暗淡，并且圖像臉部、帽沿等細節(jié)信息出現(xiàn)一定程度的模糊，整體視覺效果不太理想;相對而言，圖4d視覺效果與原始圖像圖3a最為接近，灰度動態(tài)范圍得到有效改善，清晰度優(yōu)于圖4b和圖4c。

(2)客觀分析:整體上看，無論是文獻［1］、文獻［9］還是本文濾波方法，當噪聲強度逐漸增大時，PSNR值逐漸減少、MSE值持續(xù)增大，這表明三者濾波性能伴隨噪聲方差增大而下降;當噪聲方差為0.05時，文獻［1］、文獻［9］的PSNR值均為21 dB左右，MSE也大體相當，這表明兩者對于該水平的高斯白噪聲濾波效果基本一致，并且隨著噪聲強度的增大，這樣的“一致”情形一直保持到噪聲方差處于0.20時，當噪聲方差為0.25時，兩者PSNR也僅相差1 dB、MSE值相差10左右;本文濾波方法在噪聲為0.05時，PSNR和MSE優(yōu)于文獻［1］、文獻［9］濾波方法，分別為5 dB和12～14左右，當噪聲方差增大到0.25時，本文濾波方法PSNR值仍高于其他方法2.5～3.5 dB，MSE值低于其他方法15～25 dB，這可以充分說明，本文濾波方法對于高強度的高斯白噪聲具有較好的濾波效果，其濾波性能優(yōu)于文獻［1］、文獻［9］。

2)波域增強函數(shù)系數(shù)取值分析

表4數(shù)據(jù)對不同方差的高斯白噪聲進行多項式擬合，可獲如下函數(shù)關系

式中:x為噪聲方差(v);Y(x)為系數(shù)a的取值;Y′(x)為系數(shù)b的取值。系數(shù)a和b取值大體上隨著噪聲方差的增大而持續(xù)減小，特別是系數(shù)a取值與噪聲方差成典型的線性關系，通過上面兩式可對不同噪聲強度下增強函數(shù)系數(shù)進行粗略計算，以獲得本文濾波方法在該噪聲水平下的最佳濾波效果。

3 結束語

本文針對圖像高斯噪聲，提出了一種具有增強效果的濾波算法。該算法首先通過對中值濾波進行改進，以實現(xiàn)對噪聲圖像實現(xiàn)多角度、多尺度逐級濾波處理，以濾除一部分高斯噪聲;然后對殘余噪聲圖像進行小波域逐級均值濾波;最后結合線性、非線性圖像增強方法提出了一種新型小波域增強函數(shù)對濾波后的圖像進行灰度動態(tài)范圍的改善，提高濾波后圖像的質量，并結合實驗對增強函數(shù)系數(shù)取值與噪聲方差進行多項式擬合，給出了二者的函數(shù)關系。實驗結果表明，該濾波算法對于高強度的高斯噪聲能進行一定程度的自適應濾除，抑制效果較為理想。

［1］王小兵，孫久運.一種新型高斯噪聲濾波算法［J］.北華大學學報:自然科學版，2011，12(5):606－609.

［2］NASONOV A V，KRYLOV A S.Fast super－resolution using weighted median filtering［C］//Proc.ICPR 2010.［S.l.］:IEEE Press，2010:2230－2233.

［3］賀長偉，劉英霞，任文杰，等.基于多級中值濾波的小波去噪方法［J］.計算機應用，2007，27(9):2117－2119.

［4］KUBOTA R，SUETAKE N.Threshold tuning of switching median filter employing distribution distance［C］//Proc.PSIVT 2010.［S.l.］:IEEE Press，2010，427－431.

［5］孫樹亮，王守覺.一種基于改進的極值中值濾波算法［J］.計算機科學，2009，36(6):165－166.

［6］余永維，殷國富，蔣紅梅，等.磁瓦表面圖像的自適應形態(tài)學濾波缺陷提取方法［J］.計算機輔助設計與圖形學報，2012，24(3):351－356.

［7］殷明，劉衛(wèi).基于四元數(shù)小波變換HMT模型的圖像去噪［J］.計算機工程，2012，38(5):213－215.

［8］鄭鈺輝，朱立新，王幸平，等.具有紋理保持能力的四節(jié)偏微分方程去噪方法［J］.計算機工程與應用，2009，45(7):195－198.

［9］王小兵，孫久運，湯海燕.一種高斯噪聲組合濾波方法［J］.佳木斯大學學報:自然科學版，2011，29(5):696－698.

［10］王小兵，孫久運，湯海燕.基于小波變換的圖像混合噪聲自適應濾波算法［J］.微電子學與計算機，2012，29(6):91－95.

［11］王小兵，孫久運，湯海燕.一種基于數(shù)學形態(tài)學與小波域增強的濾波算法［J］.微電子學與計算機，2012，29(7):64－67.

［12］SHEIKH H R，BOVIK A C.Image information and visual quality［J］.IEEE Trans.Image Processing，2006，15(1):430－444.

［13］WANG Zhou.Image quality assessment:from error visibility to structural similarity［J］.IEEE Trans.Image Processing，2004，13(4):600－612.