PAMF處理的抗混響應用仿真研究＊

夏 雪 張明敏 王平波

（海軍工程大學水聲電子工程系 武漢 430033）

0 引 言

隨著現代主動聲吶體制向低頻化、大功率、大孔徑方向發展，混響作為聲吶主動工作方式下特有的干擾，對水聲信號檢測性能的影響日趨凸顯.而對于載體運動的主動聲吶來說，混響的一個重要特征便是由平臺運動引起的多普勒擴展.這種擴展與機載預警雷達的雜波譜擴展特性非常相似，所以運動聲納混響的抑制可以借鑒發展較為成熟的雷達雜波抑制技術.

1973年，Brennan首先提出了空時二維雜波處理思想并用于機載雷達，其實質就是將一維空域濾波技術推廣到時間與空間二維域中.實際上，機載預警雷達面臨的雜波環境往往是非均勻的［1］，因此非均勻環境下的空時自適應處理（STAP）方法受到越來越廣泛的關注.近年來提出的參數自適應匹配濾波法PAMF［2－4］是一種與傳統空時自適應處理結構完全不同的新方法，可稱為線性預測類空時自適應處理方法［5］.

本文從匹配濾波的的角度，對空時最優處理器和PAMF處理器進行比較詳細的對比，分析了PAMF處理器的原理、結構以及性能，并指出在小樣本數情況下PAMF處理器檢測信號的優勢，并分析這種優勢產生的原理.

1 空時最優處理的匹配濾波解讀

考慮均勻線列陣的一組輸出序列：｛x（m）｜m＝0，1，…，M－1｝，x（m）∈CN×1，M 為采樣時間點數，N為陣元數，如果干擾信號xu是高斯分布的，則最優空時處理器的權矢量可以表示為：

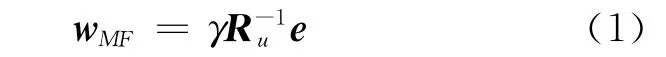
式中：γ為任意標量，不失一般性，取γ＝1；Ru＝是干擾協方差矩陣；e∈CMN×1為目標的空時導向矢量，可表示為

式中：?為Kronecker積；fd為歸一化時間導向矢量；fs為歸一化空間導向矢量，則空時最優處理器的輸出為

也可以從匹配濾波的角度來理解空時最優處理器，這時可稱為MF處理器，即匹配濾波處理器.由于Ru是一個正定厄米特矩陣，所以可以對其做LDU分解得到

式中：A∈CMN×MN為一個下三角矩陣，其主對角線上是M個單位矩陣IN；D∈CMN×MN是一個塊對角矩陣，主對角線上的元素為D（m）∈CN×N，m＝0，1，…，M－1.

即為空時最優濾波器的匹配濾波形式.其中A－1為塊白化濾波器，而為聯合方差歸一化濾波器，MF處理器結構見圖1.

圖1 MF處理器結構框圖

令Rε（m）＝E｛ε（m）ε（m）H｝為預測誤差協方差矩陣，該矩陣為正定厄米特矩陣，對其做LDU分解得

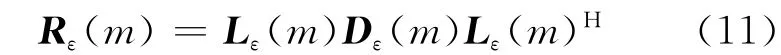
式中：Lε（m）為一個下三角矩陣；Dε（m）為一個對角線矩陣，令T（m）＝（m），PAMF處理器結構見圖2［6］.

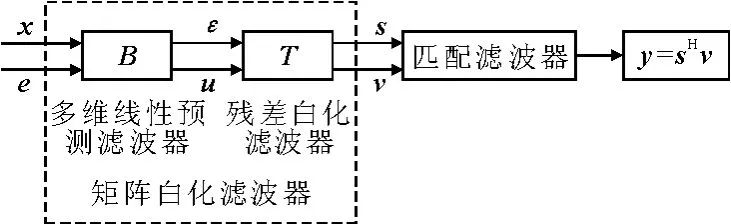
圖2 PAMF處理器結構框圖

PAMF方法利用固定的階數和模型參數來設計多維線性預測誤差濾波器和殘差白化濾波器，大大簡化濾波器設計過程，以上就是PAMF處理器的原理和結構.

PAMF處理器設計的關鍵在于求取多維線性濾波器系數，根據不同的準則有不同的求取方法，這里采用最小二乘法.

2 PAMF處理器設計

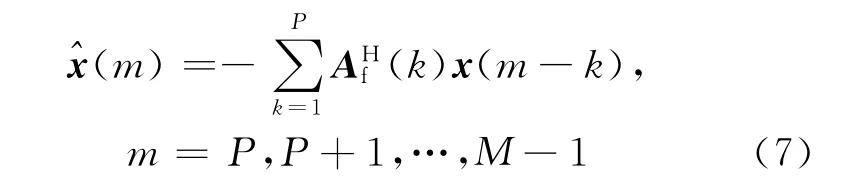
則前向線性預測誤差為

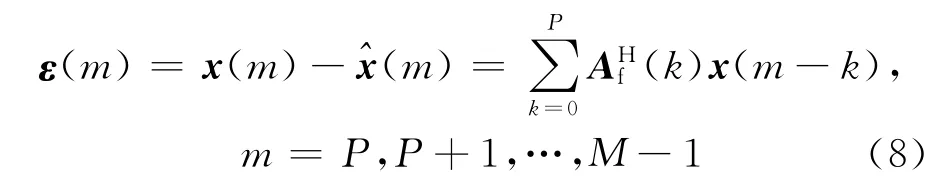
式中：Af（0）＝IN，為簡便起見，把計數起點由P改為0，并用一種更加緊湊的形式表示.

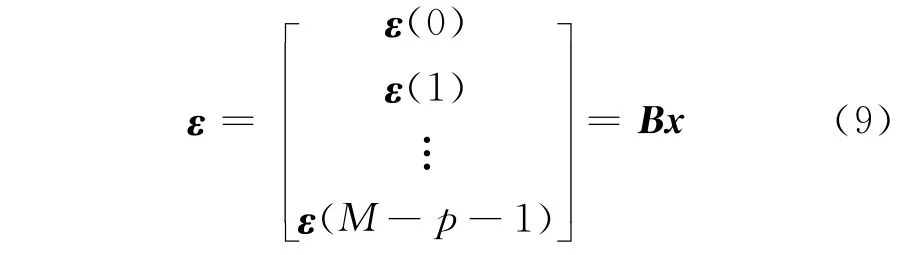
式中：

最小二乘法的目標是求得使最小的預測系數Af（p），k＝1，…，P，為此要解如下方程：

由于解方程的過程相當復雜，因此只給出結果［7］：

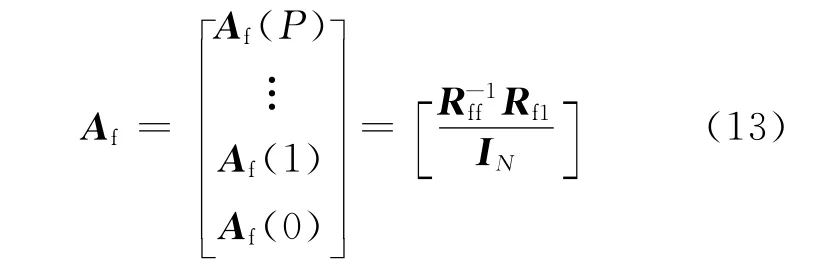
式中：Rff∈CPN×PN和Rf1∈CPN×N是矩陣Rf∈CP（N＋1）×P（N＋1）的子陣，關系如下.

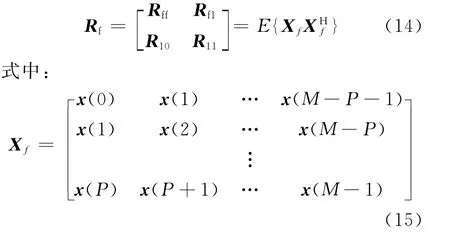
以上即為PAMF處理器的設計過程原理、結構及設計過程.

3 抗混響應用仿真實例

1） 仿真條件 仿真環境見圖3.

圖3 實驗仿真環境

仿真實驗采用如上混響仿真軟件.海底海面和體積散射源個數分別為：2 000，4 000和6 000，海底地質為泥沙底質；風速為6kn，體積散射強度為－75dB，接收放大倍數為60dB.平臺速度10kn，接收陣為115的ULA，陣元間距1個半波長，擺放位置為正側視陣；發射單頻信號頻率為750Hz，脈寬為0.1s；目標方位為60°，徑向速度為－5kn（實際速度為10kn）；信混比為0dB，噪混比為－20dB.目標與接收陣的相對位置見圖4.

圖4 仿真示意圖

2） 原始接收信號 接收陣列某一路輸出見圖5.

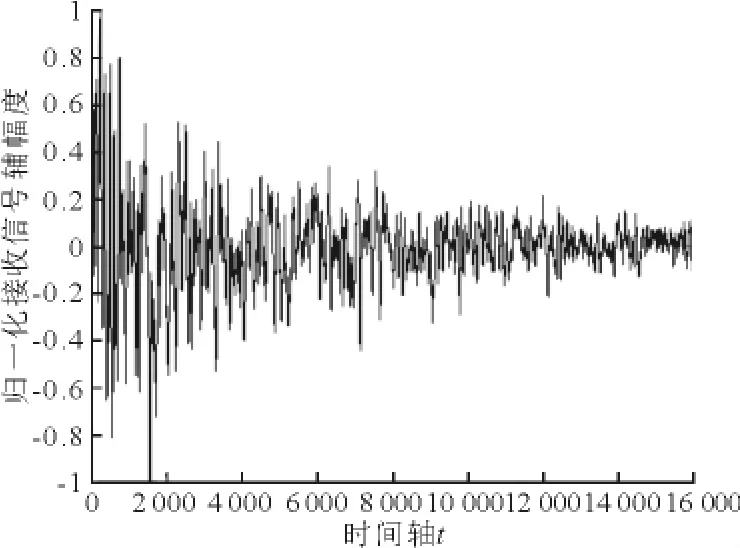
圖5 某一陣元通道接收信號幅度圖

由上圖，并不能從接收信號的波形得到目標信息，需經過處理.

3） 目標檢測性能 仿真條件如上述，當訓練樣本數為80，時間序列長度為120時，仿真結果見圖6～7.

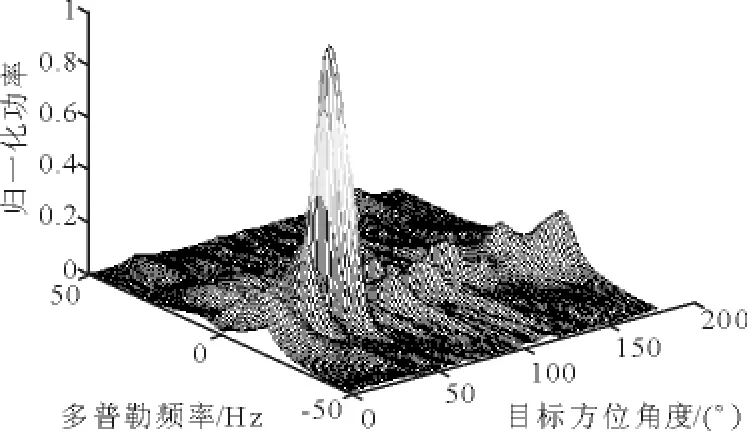
圖6 MF檢測結果（樣本數為80）

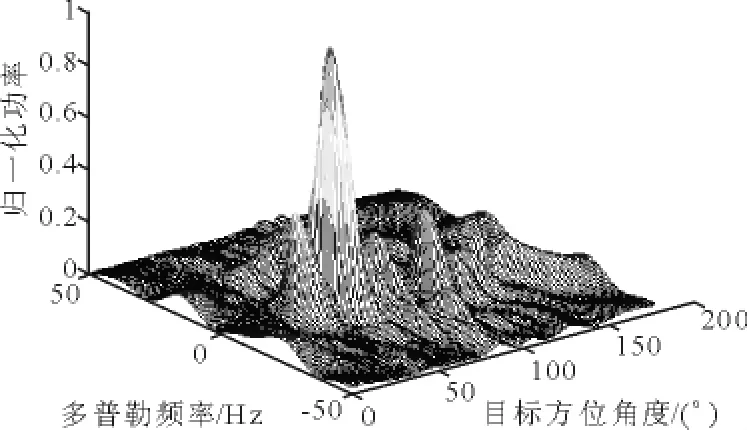
圖7 PAMF檢測結果（p＝5，樣本數為80）

目標的多普勒頻率可由以下公式計算得到

式中：va為目標與平臺的相對速度；c為聲速；f0為發射信號頻率，根據該公式可計算目標多普勒：

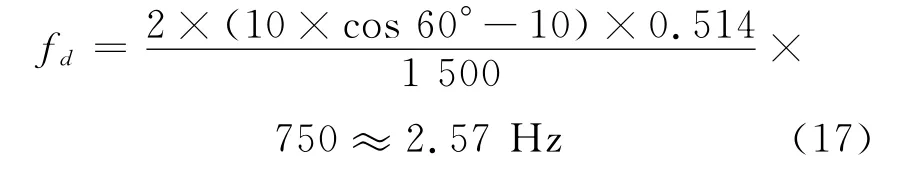
由以上2圖比較發現，在樣本充足的情況下，MF算法對干擾的抑制效果較PAMF方法好，但是二者差別不大.

在以上樣本數充足的條件下，兩種處理器的處理結果相差不大，樣本數降低到20時的處理結果見圖8～9.

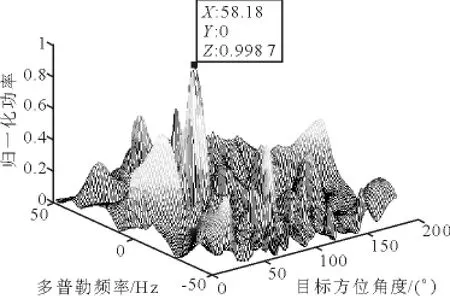
圖8 MF檢測結果（樣本數為20）

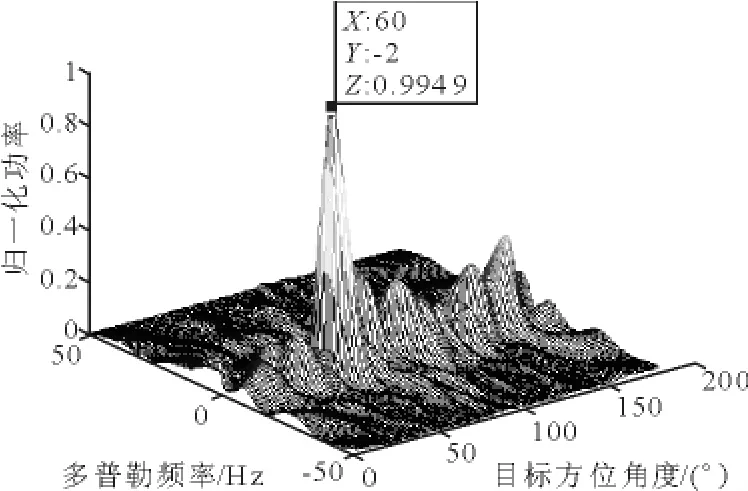
圖9 PAMF檢測結果（p＝5，樣本數為20）

由上圖可見，在小樣本數情況下，MF的檢測效果遠不及PAMF.在MF處理器的處理結果中不僅有很多干擾未得到有效抑制，并且對目標的方位和多普勒估計不準確.而PAMF處理器的處理結果與大樣本數條件下并無很大差別，目標依然清晰可見.究其原理，下一小節將進行闡述.

4 仿真結果原理解釋

一個聲吶信號檢測系統，只有當系統的自由度大于混響自由度的時候，才能準確地對目標進行估計.而混響的自由度可以由以下公式近似估算出：

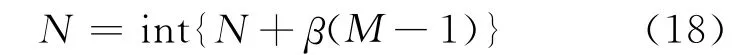
式中：N為陣元數；β為歸一化多普勒角頻率和歸一化空間角頻率的比值；M為時間序列的長度.實際上，混響的自由度往往比用上式估計出來的值高，這時可以通過觀察采樣協方差矩陣的大特征值來判斷混響自由度.Ru的特征值譜見圖10.

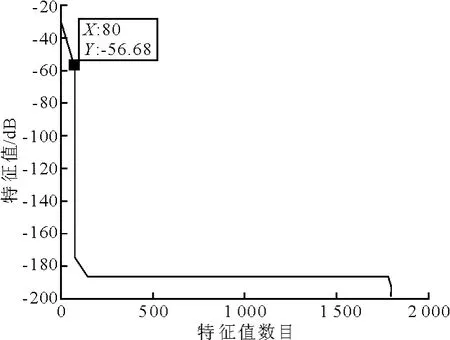
圖10 MF處理器中＾Ru的特征值譜

而PAMF處理器在低樣本數條件下依然能保持較好的目標檢測性能是因為，PAMF處理器中多維線性預測濾波器的系數Af（k）是由＾Rf而不是估計得到的，在不同的預測階數p下的特征值譜如圖11所示.

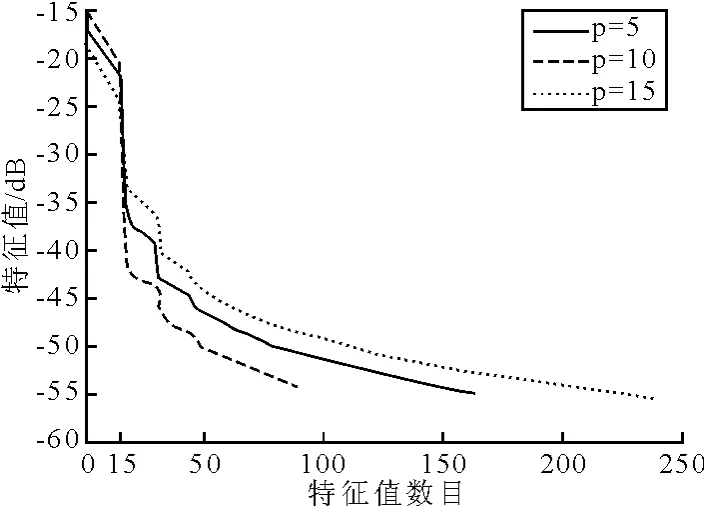
圖11 PAMF處理器中＾Rf的特征譜

5 結束語

本文描述了PAMF算法的原理、結構、設計過程以及在小樣本數條件下檢測目標的優越性，從檢測結果和處理器內部機構論證了這種優越性并解釋了其產生的原因.由于聲吶信號處理往往是處于非均勻環境，因此可用的訓練樣本數有限，而PAMF算法在小樣本數條件下依然具有很好的檢測性能這一特性適合運用于非均勻環境下的信號檢測，是一種值得深入研究應用的信號檢測處理器.

［1］王永良，彭應寧.空時自適應信號處理［M］.北京：清華大學出版社，2000.

［2］MICHELS J H，HIMED B，RANGASWAMY M.Evaluation of the normalized parametric adaptive matched filter STAP test in airborne radar clutter［C］∥IEEE International Radar Conference，Washington DC，2000：769－774.

［3］ROMAN J R，RANGASWAMY M，DAVIS D W，et al.Parametric adaptive matched filter for airborne radar applications［J］.IEEE Trans AES，Apr 2000，36（2）：678－692.

［4］MICHELS J H，ROMAN J R，HIMED B.Beam control using the parametric adaptive marched filter STAP approach.In IEEE Radar Conference［J］.Huntsville，Alabama，May 2003，405－412.

［5］吳 洪，王永良，武 文.非均勻雜波環境下線性預測類空時自適應處理性能分析［J］.自然科學進展，2007，17（1）：86－92.

［6］詹昊可.主動聲吶空時混響抑制方法研究［D］.武漢：海軍工程大學，2008.

［7］DONG Yuhan.Parametric adaptive matched filter and its modified version［J］.Institution of Electrical Engineers，2006（11）：5－30.