一種時間優化的全參考圖像質量評價算法

朱麗娟

(湖北文理學院，湖北襄陽441053)

1 引言

圖像質量評價是圖像處理系統中算法性能優劣和參數優化的重要參考，已經成為工業界和學術界的持續關注的熱點。圖像質量評價可以分為主觀評價方法和客觀評價方法兩類［1］:主觀評價方法通過實驗設計，使用人的主觀感受對圖像進行評價，存在費時、復雜、不易嵌入應用的缺點;而客觀評價方法采用算法對圖像質量進行評價，具有方便、快捷，易于解析和嵌入等優點，是當前研究的主流。

客觀質量評價方法又可以分為全參考，半參考和無參考三類［2］，其中全參考算法發展最成熟。根據算法采用的技術路線，全參考方法可分為基于誤差統計量的算法和基于HVS(人眼視覺系統)模型的算法兩大類［3］。前一類算法主要有均方誤差(MSE)、峰值信噪比(PSNR)等，這類算法的缺點是僅注重評價失真圖像和參考圖像之間的差異，并沒有考慮這些差異對人的視覺感知的影響，因而和主觀評價值之間有較大的誤差;而后一類算法［4－10］通過對HVS的某些底層特性進行建模，大大提高了圖像質量預測的準確度。文獻［5］提出了比較圖像結構上的相似程度而不是差異的結構相似算法(SSIM)，具有計算方便、評價性能較高的優點，已經在圖像增強，超分辨率重構等領域中廣泛采用;同時在SSIM算法的基礎上，出現了一系列改進算法［6－10］，它們綜合模擬了 HVS的各項特性，能夠較好地保證主客觀評價的一致性，但大都存在算法復雜、運算量大的不足。

隨著圖像評價技術在紅外圖像壓縮［11］，激光主動成像［12］等領域的應用，在保證圖像質量評價算法準確度高的同時，也對算法復雜度和處理時間提出了新的要求。針對這種需求，在標準SSIM的算法框架上，提出一種加速的全參考圖像質量評價算法。

2 結構相似性評價算法

文獻［5］利用人眼視覺系統能高度自適應的提取場景中的結構信息，提出了結構相似性評價(SSIM)算法，算法包括亮度項l(x，y)，對比度項c(x，y)和結構項s(x，y)這三個部分信息的比較，其表達式分別為:

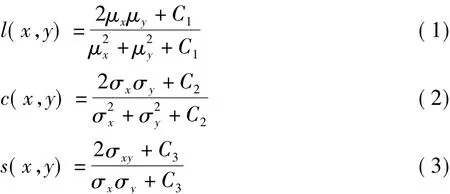
式中，μx和μy表示圖像X，Y方向的灰度均值;σx和σy表示圖像X，Y方向的灰度方差;σxy表示灰度協方差;C1，C2和C3是為了避免公式中分母為零而添加的常數。

利用以上三項信息，可以得到評價模型為:

式中，α，β，γ為各部分的相關性權重系數。

對圖像進行質量評判時，通常采用多尺度技術把圖像劃分為幾個重疊或不重疊的子塊，對每一塊利用公式(4)進行評分計算，最后得到整幅圖像的評分為:

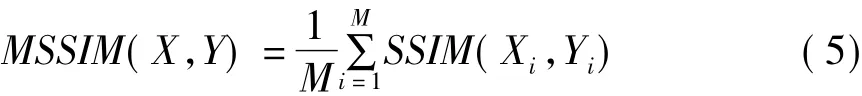
3 基于優化技術的加速算法

由于SSIM算法計算復雜、運算量較大，難于應用于對實時性要求較高的場合，因此提出基于優化技術的加速算法，對SSIM算法進行改進。

3.1 亮度項的優化計算技術

SSIM算法中亮度項的計算公式(公式(1))只含有均值項的計算，利用積分圖像技術［13］可以對亮度項的計算進行加速。

積分圖像是一種用于快速計算圖像窗口的灰度值總和或灰度均值的一種圖像中間表示，計算效率高，應用廣泛。積分圖像中任意一點的像素值ii(x，y)可以用圖1(a)所示的原始圖像相應陰影區域的灰度值總和表示，即:

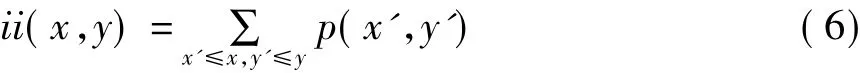
其中，p(x，y)為原始圖像中點(x，y)的像素灰度值，ii(x，y)可以用下面公式迭代計算得到:

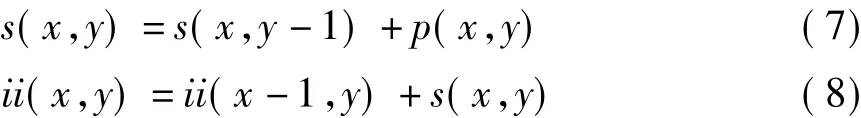
其中，s(x，y)表示一列的積分，并且 s(x，－1)=0，ii(－1，y)=0。求積分圖像只需掃描原圖像所有像素一遍，計算量很小。

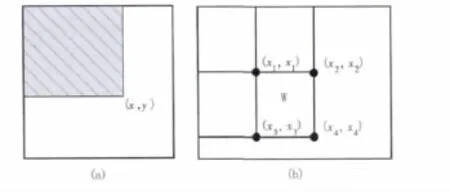
圖1 積分圖像的定義和計算原理

圖1(b)所示的窗口W的灰度值總和，對于任意大小的窗口，均可以用積分圖像中的4個相應點(x1，y1)，(x2，y2)，(x3，y3)和(x4，y4)計算得到，即窗口的灰度值總和為 ii(x4，y4)+ii(x1，y1) － (ii(x2，y2)+ii(x3，y3))。

使用積分圖像加速技術，SSIM中的亮度項的計算量將大大減少。設窗口尺寸為n×n，對于窗口的均值計算，使用高斯加權窗的標準的SSIM算法需要n2次乘法和(n2－1)次加法。而提出的積分圖像計算方法僅需要3次加法和1次減法。這樣每次窗口計算的計算減少量為save=n2(乘法)+(n2－4)(加法)－1(減法)。而計算一幅長寬為w×h為圖像，圖像中含有的窗口數為wn=(w－n+1)(h－n+1)，總的計算減少量為save×wn。因此使用積分圖像，SSIM的亮度項的計算量將大大減少。

3.2 對比度項和結構項的優化計算技術

由公式(2)、公式(3)可知，對比度項和結構項含有方差項的計算，計算代價較高。本文使用梯度幅值計算［14］來代替方差項的計算，進而對算法進行加速。

使用Roberts算子來產生梯度圖像，得到圖像的梯度逼近表示為:

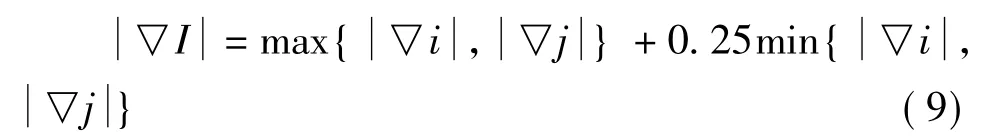
設圖像的維度為 Nx×Ny，則公式(2)和公式(3)的計算公式變為:

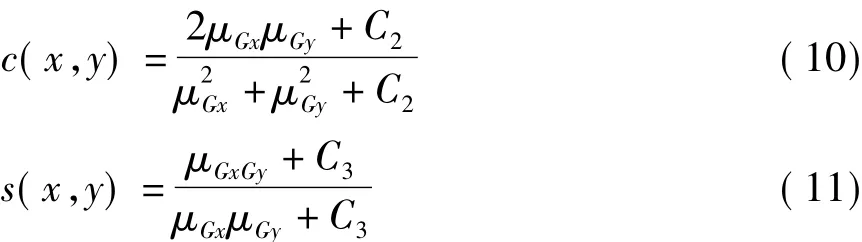
其中，μGxGy和 μGx的表達式如公式(12)，(13)所示，而μGy和μGx的表達式類似。

利用以上公式，可以得到加速的結構相似性評價(Speed Up SSIM，)公式如下:

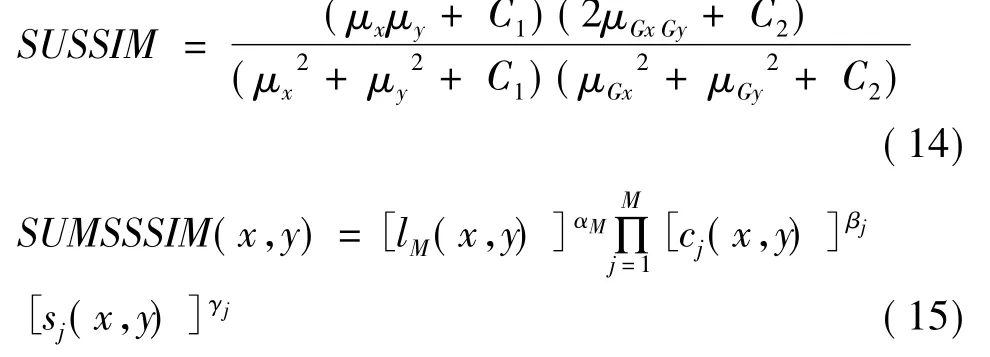
其中

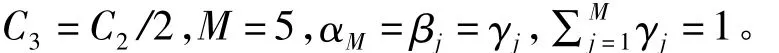
由于公式(15)為多尺度評價算法，需要采用高斯窗口和圖像塊進行子采樣得到，為了降低計算復雜度，采用8×8的整數窗口來逼近高斯窗。整數窗口的模板如圖2所示。

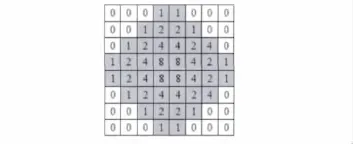
圖2 8×8整數窗口

4 實驗結果和討論

為了驗證算法的質量評價性能，采用LIVE圖像質量評估數據庫作為算法的仿真圖像。LIVE圖庫選取了29幅原始彩色圖像，5類共982幅失真模擬圖像，提供了每幅圖像的主觀評價分DMOS(Differential Mean Opinion Score)，作為客觀質量評價比較的標準。本實驗采用峰值信噪比(PSNR)和結構相似度(SSIM)，和本文提出的 SUSSIM-l(僅優化亮度項)，SUSSIM-f(全優化)進行性能指標的對比，實驗環境為Intel Core 2 Duo 2.6 GHz，Windows操作系統。

性能度量指標采用Pearson相關系數(CC)與Spearman等級相關系數(SROCC)［5］，兩個指標絕對值越接近于1，表明主客觀評價間的一致性越好。不同指標的性能指標如表1所示。

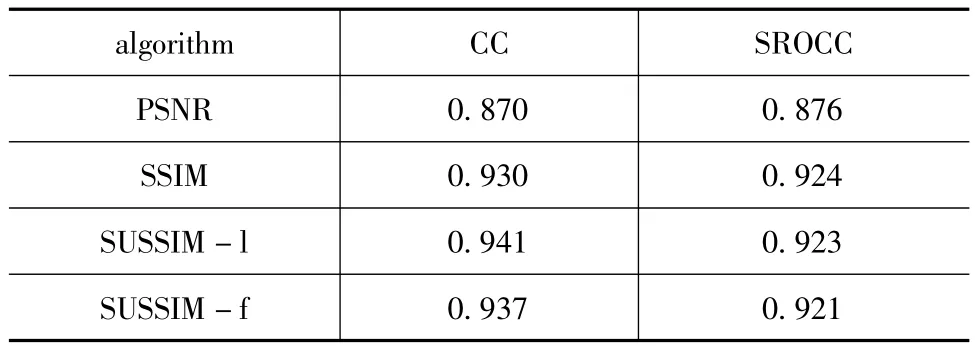
表1 算法的性能指標

從表1的數據可以看出，標準SSIM和本文改進算法，明顯優于PSNR，這是由于算法本身集成了人眼視覺系統的結構性特征的原理。而本文算法的相關系數數值和標準SSIM算法的數值非常接近，也即本文改進算法的客觀評價能力與標準SSIM相比，基本沒有損失。

為了驗證算法的加速能力，采用LIVE視頻質量評估數據庫作為仿真視頻。采用每秒處理的視頻幀數(f/s)，作為評價指標，得到幾種算法的數據表2所示。

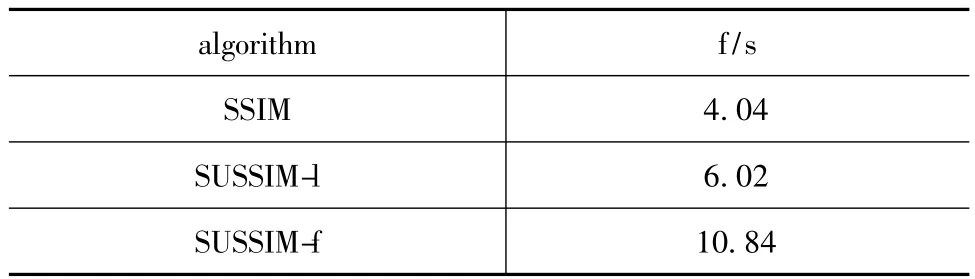
表2 算法的速度指標

從表2中的數據可以看出，本文算法(SUSSIM-f)的比標準的SSIM提高了168%。本文算法的處理速度是SSIM算法的2.68倍。

綜合表1和表2的數據，從性能/運行時間這個指標看，本文算法具有圖像質量評價能力較強，算法具有復雜度低，計算效率高的優點，適合于對實時性有較高要求的場合。

5 結論

本文提出了一種時間優化的結構相似性圖像評價算法，并在LIVE圖像庫和視頻庫上進行了仿真實驗，算法在評價一致性上和SSIM算法非常接近，而計算效率上是SSIM算法的2.68倍。算法雖然只對SSIM進行了加速和改進，但是算法的基本思想可以運用到其他的以SSIM為基礎的改進算法上來進行加速，提高計算效率。

［1］Seshadrinathan K，Soundararajan R，Bovik，et al．Study of subjective and objective quality assessment of video［J］．IEEE Trans．Image Process，2010，19(6):1427 －1441．

［2］Jieying Zhu，Nengchao Wang．Image quality assessment by visual gradient similarity［J］．IEEE Trans．Image Process，2012，21(3):919 －933．

［3］Jiang Gangyi，Huang Dajiang，Wang Xu，et al．Overview on Image quality assessment methods［J］．Journal of Electronics＆ Information Technology，2010，32(01):219 －226．(in Chinese)

蔣剛毅，黃大江，王旭，等．圖像質量評價方法研究進展［J］．電子與信息學報，2010，32(01):219 －226．

［4］E C Larson，D M Chandler．Most apparent distortion:Fullreference image quality assessment and the role of strategy［J］．Journal of Electronic Imaging，2010，19(1):1 －21．

［5］Wang Z，Bovik A C，Sheikh H R，et al．Image quality assessment:from error visibility to structural similarity［J］．IEEE Trans．Image Process，2004，13(4):600 －612．

［6］G Chen，C Yang，S Xie．Gradient-based structural similarity for image quality assessment［C］//Proc．of IEEE Int．Conf．Image Process，2006:2929 －2932．

［7］Li C，Bovik A C．Three-component weighted structural similarity index［C］//Proc．of SPIE Conference on image quality and system performance，Jan 19 – 22，2009，San Jose，California．

［8］M P Sampat，Z Wang，S Gupta，et al．Complex wavelet structural similarity:a new image similarity index［J］．IEEE Trans．Image Process，2009，18(11):2385 －2401．

［9］C Li，A C Bovik．Content-partitioned structural similarity index for image quality assessment［J］．Signal Process，2010，25(7):517 －526．

［10］ Z Wang，Q Li．Information content weighting for perceptual image quality assessment［J］．IEEE Trans．Image Process，2011，20(5):1185 －1198．

［11］ Gao Xuhui，Dong Yi，Qi Meng．Quality evaluation of impressed infrared images［J］．Laser ＆ Infrared，2008，38(10):1063 －1065．(in Chinese)

高旭輝，董怡，祁蒙．紅外圖像壓縮質量評價研究［J］．激光與紅外，2008，38(10):1063 －1065．

［12］ Dai Dede，Sun Huayan，Han Yi，et al．Image quality assessment of laser active imaging system［J］．Laser＆ Infrared，2009，39(9):986 －990．(in Chinese)

戴得德，孫華，韓意，等．激光主動成像系統目標圖像質量評價參數研究［J］．激光與紅外，2009，39(9):986－990．

［13］ Porikli F．Integral histogram:a fast way to extract histograms in Cartesian spaces［C］//Proc．of IEEE Int．Conf．Computer Vision and Pattern Recognition，2005，1:829－836．

［14］ Renting L，Zhaorong L，Jiaya J．Image partial blur detection and classification［C］//Proc．of IEEE Int．Conf．Computer Vision and Pattern Recognition，2008，1 －8．