心墻堆石壩壩坡穩定的有限元分析

賀立新

（湖南省發改委國家投資項目評審中心 長沙市 410007）

邊坡穩定分析是堆石壩設計的前提，它決定壩坡是否失穩及可能存在的破壞形式，以便為土石壩結構設計提供科學依據。 目前工程應用最廣的是需事先知道邊坡滑動面位置和形狀的極限平衡法。 在計算機和計算方法不斷發展的背景下，尤其是巖土材料彈塑性有限元計算技術的發展，應用有限元法進行邊坡穩定性分析多年來已經吸引許多工程研究人員的興趣。

本文采用大型有限元分析軟件ABAQUS，并結合強度折減法對某一堆石壩進行有限元分析，得到出塑性應變的發展及塑性區的范圍及壩坡安全系數。 計算結果表明，采用此方法進行實際堆石壩的穩定性分析是合理地，且大大提高了計算效率。

1 有限元強度折減法

強度折減法就是在有限元計算中將邊坡巖土體抗剪強度參數逐漸降低，直到土體破壞為止，其減少的倍數被定義為安全系數。強度折減法基本公式為：

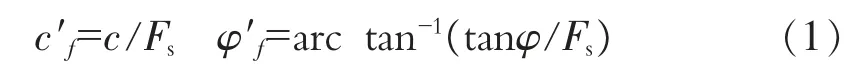
強度折減法的實質是在有限元計算中隨著材料強度參數的降低，導致部分單元應力無法和強度配套，不能承受的應力轉移到周圍土體單元中，當出現連續滑動面之后，土體破壞。 其用剪切破壞面上實際土體強度與破壞時的強度比值來定義安全系數，和傳統的極限平衡法是一致的。

2 ABAQUS在邊坡穩定分析中的運用

ABAQUS 是世界上先進的大型通用有限元分析軟件之一，得到了全球工程界和學術界廣泛接受和認可。它在材料、幾何與接觸非線性等方面的分析能力居世界領先水平，可以準確地模擬土體這種特殊材料，在解決巖土力學中復雜的非線性問題方面優勢顯著，故在巖土工程分析中得到了廣泛的應用。

2.1 本構模型的選取

正確地選擇本構模型并合理地確定計算參數是數值計算成功的前提，有限元法中巖土體本構模型一般采用與傳統極限平衡法剛塑性假設相對應的理想彈塑性模型，該模型可以分為Drucker-Prager（簡稱D-P 模型）和Mohr-Coulomb（簡稱M-C 模型）兩大類。對于M-C 模型，因其公式簡單，計算參數較容易獲取，在巖土工程數值計算中得到廣泛應用，本文選取該模型進行強度折減分析。 根據主應力以壓應力為負的規定，可將MC 準則寫成：

式中 I1、J2——分別是應力張量的第一不變量和應力偏張量的第二不變量；

θσ——應力羅德角；

c、φ——土體強度參數。

2.2 強度折減的實現

目前一些有限元軟件中，如FLAC和Plaxis 等，都已內置強度折減法。 ABAQUS 雖然沒有直接提供這種計算方法，但是實現起來也是相當方便的。首先將強度折減系數Fs定義為一個場變量，使材料參數隨場變量而變化；再指定場變量的大小，并對模型施加重力和滲透力等荷載，平衡其應力狀態，并線性增加場變量Fs，計算終止（數值不收斂）后對結果進行處理，按照失穩評價標準確定邊坡的安全系數。 通過設置場變量，使得折減過程一步到位，而不需在一個指定的折減系數計算完之后，來判定需不需要進行下一步折減，大大簡化了計算工作量。

3 工程應用

3.1 計算模型

以某一大型心墻堆石壩為例進行數值分析。 大壩典型斷面、材料特性見表1。材料分區見圖1、綜合考慮數值解不收斂、特征點位移突變以及等效塑性應變貫通作為壩坡失穩的評判標準，對該堆石壩進行竣工期和穩定滲流期的壩坡穩定性分析，得到該堆石壩各工況下的壩坡穩定安全系數和滑裂面形狀及位置。

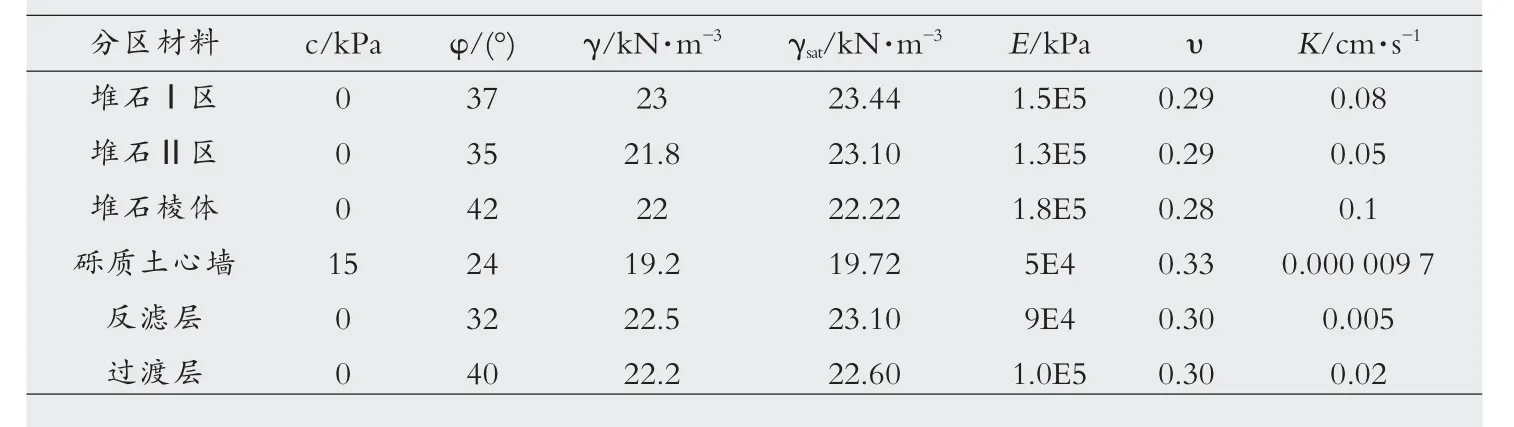
表1 壩體材料強度參數及滲透系數指標

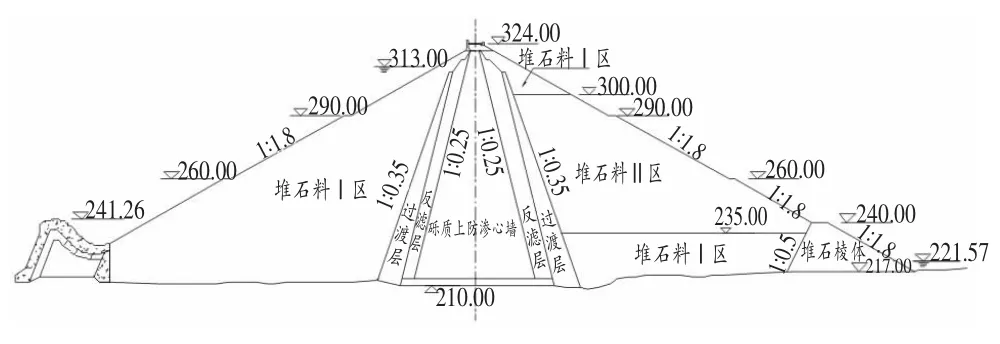
圖1 某心墻堆石壩典型斷面示意圖（m）

3.2 計算結果

采用本文方法對壩體進行穩定分析，各工況下穩定安全系數見表2。

在不考慮滲流的竣工期，從圖2～圖3 中雖然可以看出特征點位移有明顯的突變，但計算終止時位移不大（最大的位移0.027 m<<100 m），因壩高超過100 m，自然沉降等都會導致壩頂產生更大范圍的位移，故單獨采用位移突變作為邊坡臨界狀態的標準，可能會導致分析結果的失真。 計算終止時的竣工期壩體位移矢量、等效塑性應變如圖4～圖5 所示，圖中很難直觀地看出塑性區有從壩頂到坡腳貫通的趨勢，故采用等效塑性應變貫通作為邊坡失穩的判別標準也有些牽強。 根據文獻中所述內容，應綜合考慮壩體特征點位移突變、壩體塑性區貫通、計算不收斂來進行邊坡失穩的評判。 綜合考慮以上因素，取安全系數Fs=1.347。 從圖4～圖5 中還可以看出壩體上下游都出現了塑性屈服區域，塑性屈服區域成圓弧狀，有滑弧發展的動向，且滑弧很深，結果與堆石壩的一般穩定計算結果一致，符合一般計算規律。

表2 壩坡安全系數計算結果表

圖2 蓄水期安全系數Fs與水平位移的關系

圖3 穩定滲流期安全系數Fs與水平位移的關系

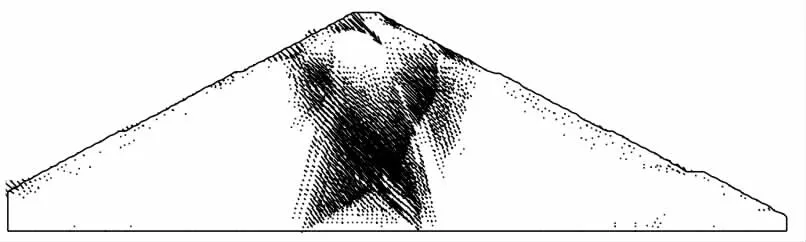
圖4 蓄水期Fs=1.347 壩體水平位移矢量圖

圖5 竣工期Fs=1.347 時壩體等效塑性應變圖

穩定滲流期時，圖3 中特征點位移在Fs<1 的時候（此時強度參數還未折減，且強度參數比實際參數更大）因受到壩體自重、滲透力的作用，出現向上游發展的趨勢；真實折減開始后（Fs>1），因土體強度參數的降低，特征點位移明顯地傾向下游。 綜合考慮壩體特征點位移突變、壩體塑性區貫通、計算不收斂對計算安全系數進行判別，取Fs=1.331，圖6～圖7給出了此時壩體的位移矢量、等效塑性應變圖。 圖中出現了兩條塑性區分布，相比竣工期，此時的塑性區明顯集中，深層滑動面更直觀、更接近圓弧形狀。此外，從圖7 中可以清楚地看到上游土體的塑性應變是由坡頂開始向坡腳逐步發展，且在壩體中間出現了密集的位移矢量和塑性區分布，塑性區分布上游比下游更直觀、清晰，同時還可以看出臨界破壞時滑裂面的形狀與一般極限平衡法的圓弧很吻合。可見，此法在分析壩坡穩定性上是直觀的、簡便的。

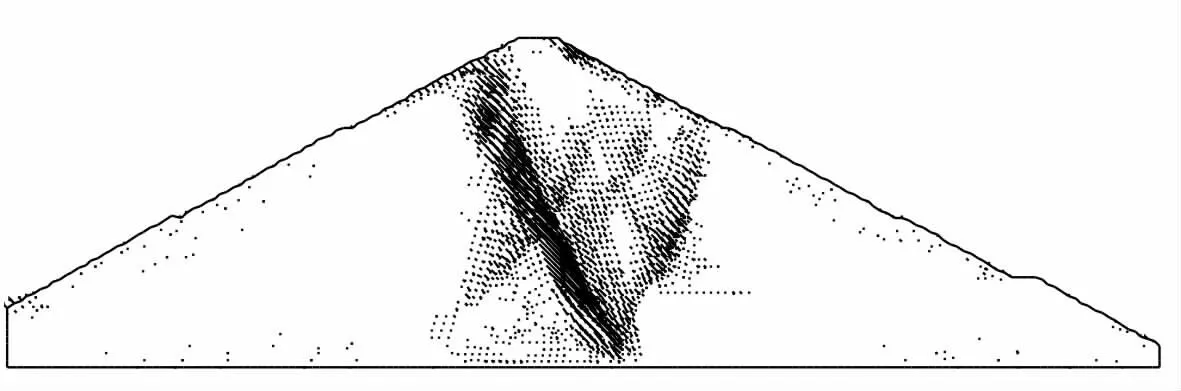
圖6 穩定滲流期Fs=1.331 時壩體水平位移矢量圖

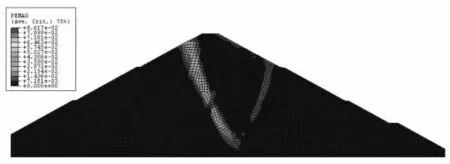
圖7 穩定滲流期Fs=1.331 時壩體等效塑性應變圖

4 結語

本文在使用強度折減法進行邊坡穩定分析時，將折減系數Fs設為場變量，直接對強度參數進行線性折減。對某一心墻堆石壩進行壩坡穩定性分析，得到各工況下安全系數；同時利用ABAQUS 軟件中強大的后處理功能，形象地描繪出邊坡失穩形態，為準確判定邊坡的真實受力狀態提供可靠依據。 結果表明，由該法所確定的穩定安全系數和滑裂面分布符合一般規律，可以推廣到考慮滲流作用的復雜土工邊值問題的基坑工程，隧洞工程等。

1 Zienkiewieo C，Humpheson C，Lewis R.W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique，1975，25（4）：671-689.

2 ABAQUS.Standard User's Manual [M].Hibbitte Karlsson&Sorenson INC，2002：26-78.

3 鄭穎人，趙尚毅.巖土工程極限分析有限元法及其應用[J].土木工程學報，2005，38（1）：91－98.

4 張培文，陳祖煜；糯扎渡大壩設計邊坡穩定的有限元分析[J].中國水利水電科學研究院學報；2003，03（12）：0207-0210.