均勻圓陣部分陣元失效情況下的DOA估計方法

張宏謀，閆劍虹，施錦文

（中國空間技術研究院西安分院 陜西 西安 710100）

在實際的DOA估計中，由于均勻圓陣（Uniform Circular Array，簡稱 UCA）具有諸多優點，比如：可對俯仰角和方位角同時進行估計，且可覆蓋較寬的頻帶，具有 360°的方位角觀察范圍；當所取的陣元數是大于5的奇數或是大于 8的偶數時，不存在取向模糊；并且，由于均勻圓陣具有對稱性，因而在各方位角上有著一樣的方向特性[1]。針對相干信號，均勻圓陣可以采用模式空間變換法[2-4]和平滑技術[5-7]來實現解相干。文獻[8]將圓陣劃分為子陣，并對其進行加權，然后進行超分辨估計。因此，它是在實際當中經常采用的一種陣列結構。但是，一旦均勻圓陣某一個或幾個通道出現故障，通道的數據變成無效數據，對于超分辨算法如MUSIC算法[9]，則會導致測向性能的嚴重惡化，甚至測向失效。

針對此問題，文中提出在均勻圓陣部分通道失效的情況下，利用均勻圓陣有效陣元數據實現對信號來波方向進行估計的方法。該方法能在部分陣元數據失效的情況下，仍然取得良好的估計性能。

1 均勻圓陣模型

設在平面內半徑為r的圓周上均勻分布著 M個相同的全向天線，參考點為陣列圓心。俯仰角φ是入射信號與z軸之間的夾角，方位角θ是入射信號沿逆時針方向與x軸的夾角。均勻圓陣的陣列模型如圖1所示。

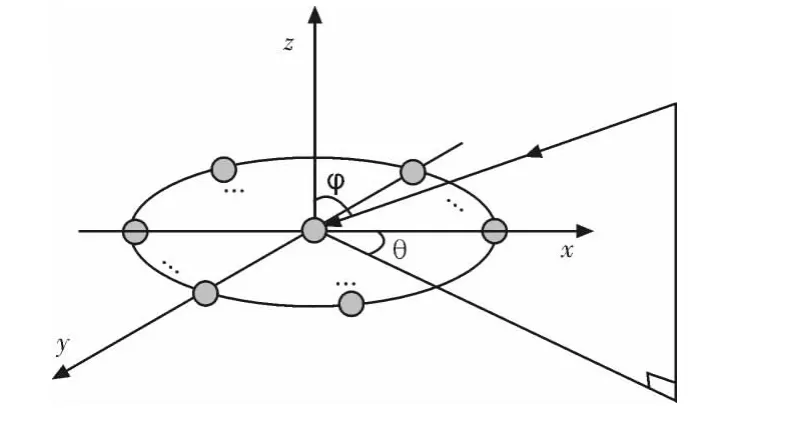
圖1 均勻圓陣模型Fig.1 Model of the UCA

均勻圓陣共有 M個陣元，共有 N個信號 si（t），i=1~N，第i個信號入射方向（θi，φi），則第 k 個陣元接收的數據為：

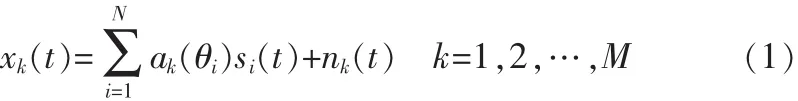
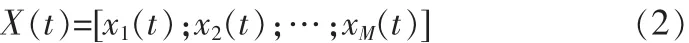
寫成矢量形式如下：

X（t）為 M×1 維快拍數據矢量，S（t）為 N×1 維信號數據矢量N（t）為M×1維噪聲數據矢量，A為空間陣列的M×N維導向矢量矩陣。其中

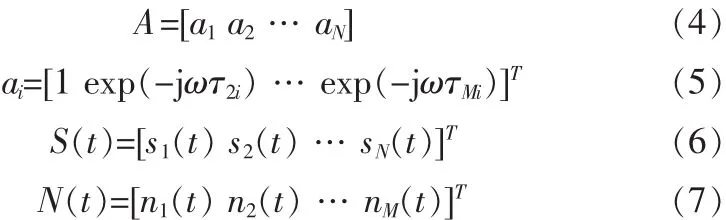
2 部分陣元失效情況下的均勻圓陣測向

2.1 均勻圓陣的MUSIC算法

MUSIC算法[10]是經典的超分辨算法，其對陣列接收數據的協方差矩陣進行特征分解，得到噪聲子空間和信號子空間，利用噪聲子空間進行譜峰搜索，進行波達方向估計。

陣列接收數據的協方差矩陣為：

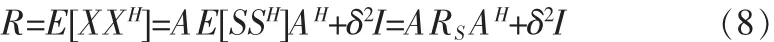
進行特征分解有:

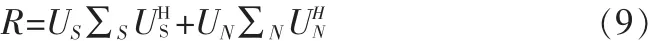
式（9）中，US是由大特征值對應的特征矢量張成的信號子空間，UN為由小特征值對應的特征矢量張成的噪聲子空間。對實際數據矩陣，數據協方差矩陣的最大似然估計為：

對R?進行特征分解，可以得到噪聲子空間特征矢量矩陣U?N。 由于噪聲的存在 a（θ）與U?N并不能完全正交，實際上是以進行方位角優化搜索實現DOA估計的。當進行一維DOA估計時，即是求 aH（θ）U?NU?HNa（θ）的最小值。 因此，MUSIC 算法的譜估計公式為：

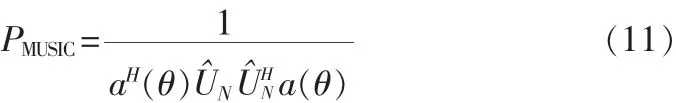
2.2 均勻圓陣隔離故障陣元測向原理

均勻圓陣用MUSIC算法測向時，一旦陣元通道出現故障，則陣元的數據變成無效數據，會導致測向性能的嚴重惡化。這是由于，對于故障陣元而言，其數據特性可能已經和正常數據的特性完全不一致，其數據的振幅，相位等有可能呈現出隨機數值的特點，尤其是相位的錯亂，是影響MUSIC算法的關鍵因素。所以，一個或幾個陣元振幅，相位的錯亂，會導致整個陣列測向性能的嚴重下降，甚至完全失效。

1）均勻圓陣隔離故障陣元分析

對于MUSIC算法而言，對于陣列的結構是沒有特殊要求的，它并不像ESPRIT算法那樣需要陣列具有旋轉不變性。也就是說，對于任意結構的天線陣列，我們都能夠用MUSIC算法進行測向，這也就是本文提出隔離故障陣元的原理所在。下面我們舉例說明。

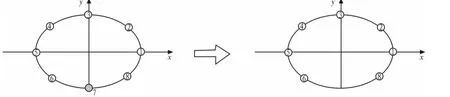
圖2 均勻圓陣故障陣元隔離原理Fig.2 Principle of isolating the failed sensor

圖2為8陣元均勻圓陣隔離故障陣列的原理示意圖。對于8陣元均勻圓陣，假定陣元7出現故障，此時，我們將其隔離后的陣列結構相當于一個7陣元面陣，此時其陣元數為7，但是已經不是均勻圓陣。由于此時陣元數目下降了1，故其可測向的信號數目最多將變為6。這也意味著陣列孔徑的損失。同理，每當故障陣元增加一個，陣列可測向的信號數目將減少一個。我們可以得到陣元故障時，陣列可測向信號的數目為：

上式中，NS為陣列可測向信號的最大數目，M為整個陣列的陣元數目，NF為故障陣元的數目。

2）構造非均勻圓陣陣列數據

由上節可知，直接將故障陣元隔離掉，可以利用部分有效陣元形成的非均勻圓陣進行測向。下面說明利用剩余的有效陣元構造接收數據的方法。我們仍然以8陣元為例進行說明。設陣列為8元均勻圓陣，故障陣元為7號陣元，則利用其余有效陣元構成的陣列數據如下：

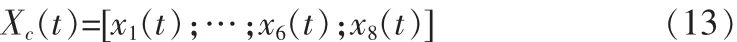
其中，Xc（t）為重構的數據矩陣，Xi（t）為第 i個陣元的接收數據。此時，由于陣元數目少一個，數據的結構在陣元的維數上較之原陣列要少一維，所以整個陣列的數據矩陣行的維數較原陣列要少一維。

3）利用構建的7元面陣測向

假定只進行方位角測向，即認為俯仰角為90°，得到MUSIC測向算法如下：

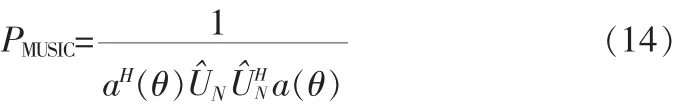
其中：a（θ）=[exp（-jω0τ1）]exp（-jω0τ2）… exp（-jω0τ6）exp[（-jω0τ8）]T，τi為第 i個陣元相對于參考陣元的時延。 因此，我們構造的7陣元面陣和原8陣元相比較，其陣列結構發生變化，在進行譜峰搜索的過程中，其導向矢量也應該相應的做出調整，不能以原導向矢量進行測向。

3 性能仿真

為簡化分析，我們以一維方位角測向進行仿真實驗。不失一般性，陣列采用8元均勻圓陣，陣元間距采用最高頻率的半波長，即 d=λ/2，快拍數為 500。

仿真實驗1：8陣元中3陣元故障對測向的影響

1）3 陣元故障性能。陣元 2，5，7 故障，信號數目為 3，來波方向為[50，120，245]°。 噪聲為加性高斯白噪聲，信噪比 10 dB，取50次獨立試驗的均值。仿真中故障陣元數據采用隨機數據，其方差等于信號功率。其仿真結果如圖3（a）所示，當陣元2，5，7故障時，空間譜估計完全失效；而沒有故障時，陣列的測向性能優良。

2）隔離3故障陣元時的測向性能。從圖3（b）中可以看出，隔離故障陣元后的陣列測向性能良好，能夠精確的測出所有3個信號的方位。

仿真實驗2：8元均勻圓陣與重構陣列測向精度的比較

設有一感興趣信號，波達方位角為45°，現考慮在不同信噪比條件下，真實陣列無故障時和陣元2，5，7故障時本文重構陣列的測向精度。仿真進行50次獨立試驗，50次仿真的誤差均值結果如圖4（a）所示。可以看到，故障陣列按照本文方法重構后的測向性能在信噪比較低時略差于陣列無故障時測向性能。而在信噪比較高時，二者測向性能一致。

圖4（b）為兩種算法在不同信噪比下的均方根誤差。與誤差性能相似，在較低信噪比條件下，本文算法的均方根誤差略大于原陣列，當信噪比較高時，二者測向性能一致。因此，本文算法具有較好的估計精度及魯棒性，其在低信噪比條件下仍然能夠實現優良的估計性能。

4 結 論

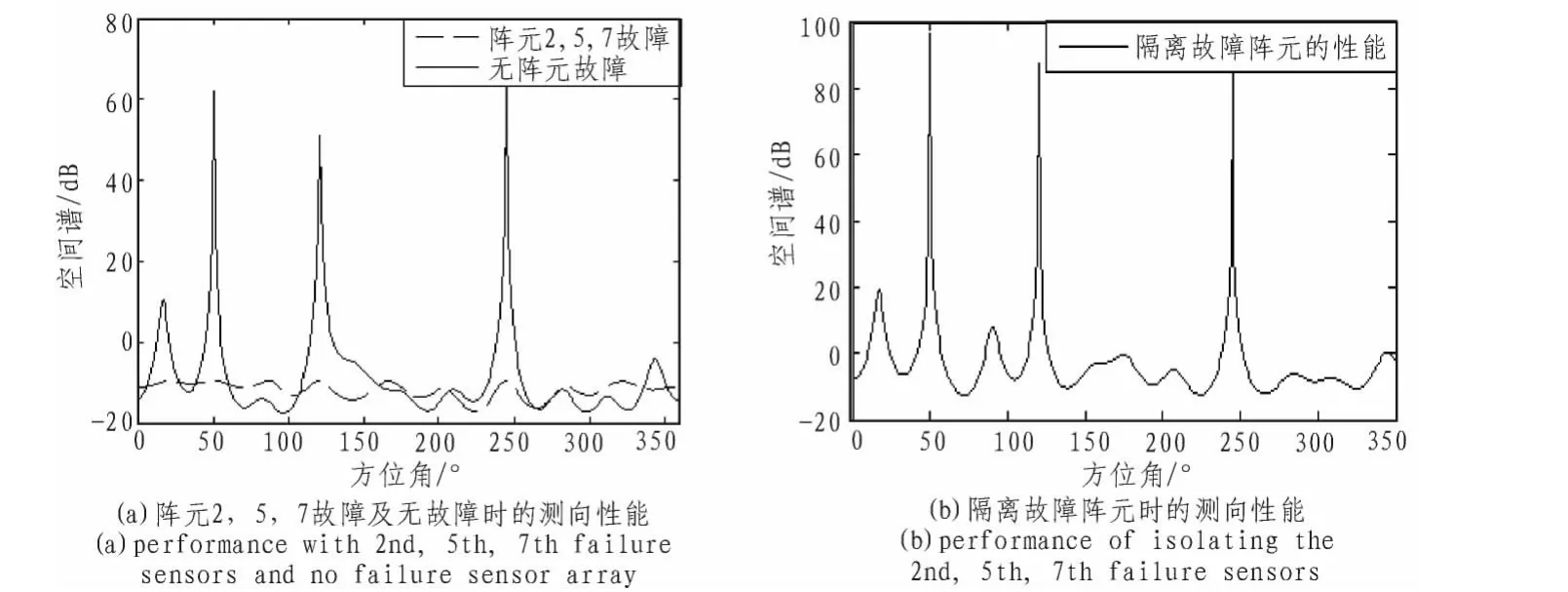
圖3 陣元故障時對陣列測向的影響Fig.3 Influence of failed sensor to the performance of array

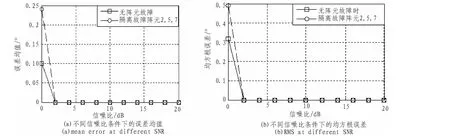
圖4 重構陣列和原陣列精度比較Fig.4 Accuracy difference between the reconstructed array and the original array

文中對在均勻圓陣部分通道失效的情況下，利用均勻圓陣[11]有效陣元數據實現對信號來波方向進行有效估計的方法進行了理論上的分析和仿真實驗的驗證。其通過對實際陣列的故障陣元進行隔離，利用剩余陣元的數據，進行高分辨的MUSIC算法測向。該方法能在較高信噪比條件下實現和原陣列幾乎相同的估計精度，在較低信噪比、信號數較小的條件下，也能取得良好的估計性能，大大增強了整個陣列譜估計的穩健性和魯棒性，計算機仿真對該方法的有效性進行了驗證。

[1]劉艷.基于均勻圓陣的波達方向估計算法的性能研究[D].重慶:重慶大學，2011.

[2]Wax M，Sheinvald J.Direction finding of coherent signals via spatial smoothing for uniform circular arrays[J].IEEE Trans on Antenna and Propagation，1994，42（5）:613-619.

[3]韓曉東，刁鳴.沖擊噪聲背景下均勻圓陣相干信源的DOA估計[J].應用科技.2012.39（1）:35~38

HAN Xiao-dong，DIAO Ming.DOA estimation of uniform circular array and coherent sources in an impulsive noise environment[J].Applied Science and Technology，2012，39（1）:35-38.

[4]楊海洋，王東進，陳衛東.一種模式空間中的快速DOA估計算法[J].中國科學技術大學學報，2010，40（8）：771-775.

YANG Hai-yang，WANG Dong-jin，CHEN Wei-dong.A fast approach to DOA estimation within mode space[J].Journal of University of Science and Technology of China，2010，40（8）：771-775.

[5]Shan T J，Wax M，Kailath T.Adaptive beamforming for coherent signals and interference[J].IEEE Trans.on ASSP，1985，33（3）:527-536.

[6]Williams R T，Prasad S，Mahalanbis S K，et al.An improved spatial smoothing technique for bearing estimation in a multipath environment[J].IEEE Trans.on ASSP，1988，36（4）:425-432.

[7]董玫，張守紅，吳向東，等.一種改進的空間平滑算法[J].電子與信息報，2008，30（4）:859-862.

DONG Mei，ZHANG Shou-hong，WU Xiang-dong，et al.An improved spatial smoothing technique[J].Journal of Electronics&Information Technology，2008.30（4）:859-862.

[8]蘇成曉，羅景青.一種均勻圓陣子陣干擾抑制DOA估計算法[J].信號處理，2010，26（9）:1355-1360.

SU Cheng-xiao，LUO Jing-qing.A novel DOA estimation algorithm via subarray jamming suppression based on uniform circular array[J].Signal Processing，2010，26 （9）:1355-1360.

[9]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Trans.on AP，1986，34（3）:276-280.

[10]王永良，陳輝，等.空間譜估計理論與算法[M].北京：清華大學出版社，2004.

[11]黃珂.均勻圓陣列參數分析[J].電子科技，2012(5):8-9,13.

HUANG Ke.Analysis of uniform circular array parameter[J].Electronic Science and Technology，2012（5）:8-9,13.