圖G（p，q）的生成子圖的構(gòu)造與計(jì)數(shù)

吳建強(qiáng) 侴萬(wàn)禧

（1.安徽理工大學(xué) 理學(xué)院，安徽 淮南 232001；2.安徽理工大學(xué) 土木建筑學(xué)院，安徽 淮南 232001）

0 引言

在各種各樣的圖中，有一類簡(jiǎn)單的，但卻是重要的圖，就是所謂的“樹”。它是基爾霍夫在解決電路理論中求解聯(lián)立方程問(wèn)題時(shí)首先提出來(lái)的，可惜他的發(fā)現(xiàn)超越了時(shí)代而長(zhǎng)期沒(méi)有引起重視。樹與圖中其他一些基本概念，如回路、割集等有密切的聯(lián)系，是圖論中比較活躍的領(lǐng)域。在圖論中，解決一些懸而未決的問(wèn)題往往首先從樹這類圖入手。許多問(wèn)題對(duì)一般的圖未能解決或者沒(méi)有簡(jiǎn)便的方法，而對(duì)于樹，則已完滿解決，且方法較為簡(jiǎn)便。

給定一個(gè)無(wú)向圖G，若G的一個(gè)生成子圖T是樹，則稱T為G的生成樹。圖的生成樹不是唯一的。但任何連通圖至少有一顆生成樹。所有生成樹中具有最小數(shù)的生成樹稱為最小生成樹，求最小生成樹是實(shí)際問(wèn)題的需要，例如“為了把若干城市連接起來(lái)，設(shè)計(jì)最短通信線路”，“為了解決若干居民點(diǎn)供水，要求設(shè)計(jì)最短的自來(lái)水管線路”等等。

1 基本思路

定義1 設(shè)G（p,q）為p個(gè)頂和q個(gè)邊的任意連通圖，則G（p,q）中任意p-1個(gè)邊所導(dǎo)出的S（G）個(gè)子圖稱為生成子圖。

定義2 設(shè)圖G(p,q)中存在S(G)個(gè)生成子圖，則S（G）個(gè)生成子圖中T（G）個(gè)不含圈的生成子圖稱為生成樹，C（G）個(gè)含圈的生成子圖稱為含圈的生成子圖，并有 S（G）=C（G）+T（G）。

定理1 設(shè)G（p,q）為任意連通圖，則G（p,q）中任意p-1個(gè)邊所導(dǎo)出的生成子圖的個(gè)數(shù)為

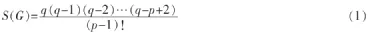
S（G）個(gè)生成子圖中含圈的生成子圖的個(gè)數(shù)為

S（G）個(gè)生成子圖中不含圈的生成樹的個(gè)數(shù)為

式中：Ci（G）—圖 G（p,q）中 Ci的個(gè)數(shù)；個(gè)邊中任取p-j個(gè)邊的選擇數(shù)。

證明：不失一般性，設(shè) G（p,q）為 p＝4，q＝6 的完全圖 K4，且 K4中 C3的個(gè)數(shù) C3（G）＝4；C4的個(gè)數(shù) C4（G）＝1，若定理 1 為真，則 K4中 P—1=3個(gè)邊所導(dǎo)出的生成子圖的個(gè)數(shù)

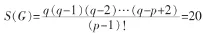
S（G）＝20個(gè)生成子圖中含圈的生成子圖僅與圈C3有關(guān)系，故含圈的生成子圖的個(gè)數(shù)為

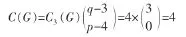
S（G）＝20個(gè)生成子圖中不含圈的生成樹的個(gè)數(shù)為

定理1得證。

定理2設(shè)G（p,q）為任意連通圖，則G（p,q）中p-1個(gè)邊所導(dǎo)出的S(G)個(gè)生成子圖的構(gòu)造歸結(jié)為

b＝S（G），v＝p，r＝A，k＝p－1，λ＝B 的（b，v，r，k，λ）設(shè)計(jì)中 S(G)個(gè)區(qū)組的構(gòu)造。由于G（p,q）中q個(gè)邊的編號(hào)為區(qū)組的變?cè)琒(G)個(gè)生成子圖與S(G)個(gè)區(qū)組一一對(duì)應(yīng)，C（G）個(gè)含圈的生成子圖與C（G）個(gè)區(qū)組一一對(duì)應(yīng)，T（G）個(gè)生成樹與 T（G）個(gè)區(qū)組一一對(duì)應(yīng)，且有 S（G）＝C（G）＋T（G）

證明：不失一般性，設(shè)則 G（p,q）為 p＝4，q＝6 的完全圖 K4，若定理2 為真，則完全圖 K4的個(gè)生成子圖的構(gòu)造歸結(jié)為 b＝20，v＝p＝4，r＝6，k＝p－1＝3，λ＝4 的（b，v，r，k，λ）設(shè)計(jì)中下列 0個(gè)區(qū)組 ：（1，2，3），（1，2，4），（1，2，5），（1，2，6），（1，3，4），（1，3，5），（1，3，6），（1，4，5），（1，4，6），（1，5，6），（2，3，4），（2，3，5），（2，3，6），（2，4，5），（2，4，6），（2，5，6），（3，4，5）,(3,4,6),(3,5,6),(4,5,6)的構(gòu)造，當(dāng)K4中q=6個(gè)邊的編號(hào)被確定后，S(G)=20個(gè)生成子圖與20個(gè)區(qū)組一一對(duì)應(yīng)，20個(gè)生成子圖中有4個(gè)含圈的生成子圖，有16個(gè)不含圈的生成樹。 亦即：T（G）＝16，C（G）＝4 且

S（G）＝C（G）＋T（G），見圖 1。 定理 2 得證。

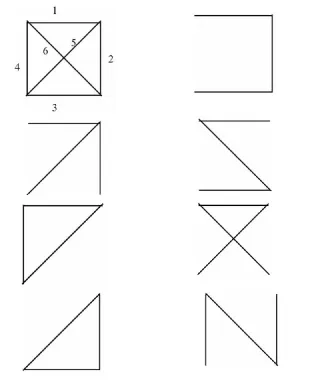
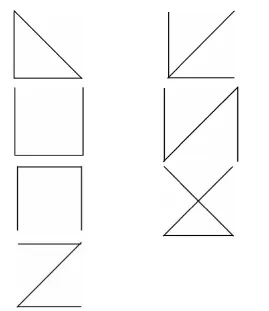
圖1

2 八面體平面的生成子圖

1）生成樹的個(gè)數(shù)

設(shè)圖 G（p,q）為 p＝6，q＝12 的八面體平面圖，圖 G（6，12）中的 C3的個(gè)數(shù) C3（G）＝8，C4的個(gè)數(shù) C4（G）＝15，C5的個(gè)數(shù) C5（G）＝24，則據(jù)定理 1，圖 G（6，12）中生成子圖的個(gè)數(shù)為

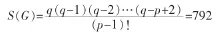
S（G）＝792個(gè)生成子圖中含圈的生成子圖的個(gè)數(shù)C（G）＝393

S（G）＝792個(gè)生成子圖中不含圈的生成樹的個(gè)數(shù)為：

2）S（G）個(gè)生成子圖的構(gòu)造

G（6，12）中 S（G）＝792 個(gè)生成子圖可借助于 b＝792，r＝330， k＝5，λ＝120 的下列區(qū)組的（b，v，r，k，λ）設(shè)計(jì) ：（1，2，3，4，5）（1，2，3，4，6），（1，2，3，4，7），（1，2，3，4，8），（1，2，3，4，9），（1，2，3，4，10），（1，2，3，4，11），（1，2，3，4，12），（1，2，3，5，6），（1，2，3，5，7）…(8,9,10,11,12)。 當(dāng)圖 G（6，12）中q＝12個(gè)邊的編號(hào)被確定后，792個(gè)區(qū)組中的399個(gè)區(qū)組與399個(gè)生成樹一一對(duì)應(yīng)，792個(gè)區(qū)組中的393個(gè)區(qū)組與393個(gè)含圈的生成子圖一一對(duì)應(yīng)，且有 S（G）＝C（G）＋T（G）的關(guān)系。 這說(shuō)明：生成樹的個(gè)數(shù)的結(jié)算結(jié)果與實(shí)際構(gòu)造想吻合。

3 結(jié)束語(yǔ)

由于Cayley公式僅適用于任意完全圖Kp中生成樹個(gè)數(shù)的計(jì)算。而任意非完全圖中的生成樹的計(jì)算問(wèn)題，可以運(yùn)用本文方法來(lái)解決，盡管計(jì)算繁瑣，但卻解決了任意圖生成樹的構(gòu)造。任意平面中的生成樹在遙控技術(shù)等領(lǐng)域有著廣泛的應(yīng)用，根據(jù)本文的思想，一種基于森林分解的生成樹的構(gòu)造和計(jì)數(shù)方法將能夠得到，也必將得到廣泛的運(yùn)用。

［1］Bollobasb.Graph Theory[M].New York：San Francisco,Academic Press,1978.

［2］Freds.Roberts BarryTesman.Applied Combinatorics[M].beijing：China Machine Press,2007.

［3］侴萬(wàn)禧.完全圖的生成樹的構(gòu)造與計(jì)算[J].山東師范大學(xué)學(xué)報(bào)：自然科學(xué)版,2007,11(4)：72-72.

［4］侴萬(wàn)禧.任意的生成樹的構(gòu)造與計(jì)數(shù)[J].山東師范大學(xué)學(xué)報(bào)：自然科學(xué)版,2008,23(1)：14-15.

［5］侴萬(wàn)禧,郝朋偉.完全二分圖的生成樹的個(gè)數(shù)[J].阜陽(yáng)師范學(xué)院學(xué)報(bào),2008,25(4)：12-14.

［6］侴萬(wàn)禧,等.平面的四著色與對(duì)偶圖的H圈[J].沈陽(yáng)師范大學(xué)學(xué)報(bào)：自然科學(xué)版,2009,27(3)：264-266.

［7］徐俊明.圖論及其應(yīng)用[M].中國(guó)科學(xué)技術(shù)大學(xué)出版社,2004.

［8］侴萬(wàn)禧.2t名運(yùn)動(dòng)員的循環(huán)賽和對(duì)集的劃分[J].安徽理工大學(xué)學(xué)報(bào)：自然科學(xué)版,2006,26(1)：64-69.

［9］侴萬(wàn)禧.邊矩陣K2n+1的k+1-邊著色與循環(huán)賽的安排[J].安徽建筑工業(yè)學(xué)院學(xué)報(bào)：自然科學(xué)版,2006,14(4)：1-5.

［10］侴萬(wàn)禧,林雨.12 面體中的 H 圈[J].揚(yáng)州大學(xué)學(xué)報(bào)：自然科學(xué)版,2007,10(4)：32-38.