水砂充填采礦中采場內充填體滲流問題研究*

毛彥鑫 丁凌霄 馮朝朝

(中國礦業大學礦業工程學院)

充填采礦由于回采安全、資源回收率高、對地表生態破壞小等優勢，日益獲得人們的青睞，加之近年充填開采過程的許多復雜工藝實現了機械化和自動化，充填采礦將成為未來地下金屬礦床開采發展的主要趨勢［1］。水砂充填采礦法是將選礦廠尾砂或者河砂通過水力管路以一定濃度從地表輸送至采場進行采空區充填的一種采礦方法。水力輸送過程中要求充填料漿含水較高，以便提高輸送速度，防止堵管。在充填采場內多余的水通過預先布置的脫水井重力自流疏干，要求疏干時間盡可能短，以便滿足接續作業的支撐強度要求。充填體的疏水時間與其滲流特性密切相關，因此，充填體滲流特性的研究對于生產人員選擇合理的尾砂粒徑、充填層厚度和脫水井布設間距、提高疏水效率有重要意義。

1 滲流時間模型的建立

1.1 理論解算模型

一般情況下，充填采場內會按一定的間排距布設脫水井，含水較高的水砂充填料漿進入采場后，多余的水分通過重力自流至脫水井內，從脫水井下部預設的管路排出。由于上向水平分層充填采礦法中充填層的厚度不大，而且在疏水過程中充填體上方沒有受到外部應力的作用，其滲流規律類似于地下水滲流中無壓含水層的非穩定流。它的頂部邊界是潛水面，在非穩定流的過程中潛水面的位置也在不斷變化(降低)，因此假設的單元體如圖1所示［2-3］。

但是要精確求解此類問題比較困難。充填體內水的滲流是流向脫水井的，從其流動剖面可以看出，潛水面是一條曲線，過水斷面也是曲線，在該曲線上任一點的流速qs是處處相等的。由于滲流流動的水面坡降很小，可以采用裘布依假設(圖2)近似求解［4］，即假定在垂直過水斷面上任一點的流速是處處相等的，而且流線均為平行直線。

在流線上，水流的流動服從達西定律，有

式中，φ=p+ρg z，由于充填體上部無外部應力，故p=0。記 h= ρg z，有

由圖2可知，d x和d s之間存在一個夾角θ，則有

當 θ→0，則tanθ→0，sinθ→0，即有sinθ≈tanθ，式(2)可變為

即在水的滲流過程中，忽略了z方向的流速分量，把實際剖面流是x、y、z三維流動問題簡化為x、y二維問題。

按照質量守恒的原理，在無源匯項的情況下，有

式中，K為充填體的滲流系數，S為比儲水系數，h為水頭高度。式(4)可變換如下:

滲透系數K和比儲水系數S均為常數，有

又

式(6)可變換為

由于充填體為顆粒均勻的尾砂或河砂，所以可將其簡化為一維問題求解，去掉式中含有y的項，有

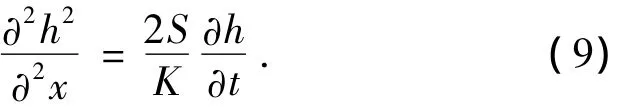
故最終數學模型確定為

令K/S=N，則有

利用有效容積法對非線性微分方程進行離散，對i=1～m，有m×m的矩陣方程:

式中，

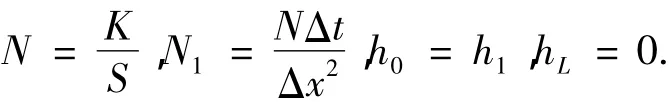
1.2 數值計算模型

對非線性微分方程進行離散之后，得到式(11)，其中的滲透系數K、比儲水系數S和充填體厚度hi在特定的礦井生產條件下是相同的，因此在方程中均作為常數來處理。用MATLAB編寫計算程序，采場內充填體的疏水模型如圖3所示。

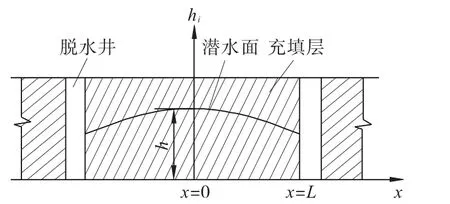
圖3 數值計算脫水模型hi—充填層厚度，m;h—潛水面高度，m;x—疏水距離，m

2 滲流特性參數實驗測定

由于滲透系數表征充填體的滲流特性，比儲水系數表征充填體的固結特性，所以在實驗室采用SLB－1型應力應變控制式三軸剪切滲透試驗儀對所采集尾砂進行滲流和固結試驗，試驗裝置原理如圖4所示。

圖4 測試裝置原理

2.1 滲透系數測試原理

由于充填采場內充填體的水滲流屬于重力自流，并無很大的外部應力作用于充填體，因此不考慮實際流動過程中可能發生的非線性特性，仍沿用經典滲流力學中達西定律的表述方式

在式(12)中，假定孔隙壓力梯度是均勻的，即

這里p1，p2表示的是試樣兩端的孔隙壓力，L表示試樣的長度。而流量Q是容易測量的，所以滲流速度q可以由計算得到。這樣滲透系數就可以根據滲流速度和孔隙壓力梯度的值，并應用達西公式計算得出。基于以上假定，得到的滲透系數是1個常數。

2.2 比儲水系數測試原理

在經典滲流力學和地下水文學等工程學科中，將比儲水系數定義為孔隙流體壓力下降(或升高)1個單位時，從多孔介質中排除(或吸收)的水的體積［5］。在這里，假定尾砂顆粒是不可壓縮的彈性體，那么從外部測得的多孔介質體積變化就是孔隙體積變化。

對于多孔試樣，有

式中，Vt為多孔介質體積，Vs固體(尾砂顆粒)體積，Vp孔隙體積。

在假設固體顆粒不可壓縮的條件下，

又 Vp=nVt，有

式(16)就是比儲水系數測試的原理方程，式中總應力

且

σr、σθ、σz分別為潛水面徑向、切向、z向應力;ΔVp就等于排出三軸腔的水量;Kp、αp是由實驗確定的參數。

將式(16)變換得到

考慮到充填體松散易變形的特性，現將比儲水系數定義為總應力增加1個單位，孔隙壓力下降1個單位，從充填體中排出的水量。令Kp=1，αp=1，即為充填體的比儲水系數，有

3 滲流效率模擬及分析

以中國有色集團紅透山銅礦為例，紅透山銅礦采用上向分層水砂充填采礦法開采礦石，為了滿足生產接續的要求，需要充填采場內多余水份快速疏干，以滿足接續作業對充填體強度的要求。

采集現場充填尾砂，通過實驗室測定其滲透系數和比儲水系數，結合生產現場充填采場內充填層厚度和脫水井的布設間距，研究各個參數對滲流效率的影響及充填體的滲流特性。

保證其他參數不變的情況下，改變其中的1個參數，得出某一特定參數影響下充填采場內充填體的滲流效率曲線，見圖5～圖8。圖9為充填體內水滲流潛水面隨時間的變化曲線。

圖5 滲透系數與滲流時間的關系

圖6 比儲水系數與滲流時間的關系

圖7 充填層厚度與滲流時間的關系

圖8 脫水井間距與滲流時間的關系

由圖5可以看出，隨滲透系數不斷增大，充填體滲水效率也逐漸提高，滲流時間逐漸縮短，故增大充填料的粒徑有助于提高充填體脫水效率。由圖6可知，比儲水系數與充填體的滲流效率成正比，比儲水系數越大，充填體的滲流時間越短。圖7表明，由于分層充填采礦中充填層厚度本身較小，重力壓降不大，故充填層厚度對滲流效率的影響不大。圖8說明充填井布設間距越小，所需脫水時間越短，故在經濟合理的條件下，應當適當減小脫水井的設置間距。

圖9 充填體中潛水面隨時間的變化曲線1—1 h;2—8 h;3—16 h;4—24 h;5—2 d;6—3 d;7—4 d;8—5 d;9—6 d;10—7 d

圖9 為充填體內水分疏干的滲流規律，可以看出充填體中潛水面隨時間不斷下降，但是當水頭高度越小時，單位水頭下降所需的時間越長，這是由于重力壓降也隨之減小的緣故。這也是滲透系數、脫水井布設間距與滲流時間的關系為非線性的原因。

4 結論

(1)建立充填體滲流的微分方程，利用有效容積法進行離散后得到矩陣方程，并用MATLAB編制了數值計算程序。

(2)給出了實驗室準確測定滲流系數和比儲水系數的基本原理和方法。

(3)通過改變單一參數得到特定參數與充填體滲流效率的關系曲線，結果表明:滲透系數越大、比儲水系數越大、脫水井布設間距越密，滲流效率就越高。充填層厚度對滲流時間的影響不大。因此，為了實現充填體的快速脫水，應當適當增大充填料的粒徑、減小脫水井的布設間距。

(4)本研究未就充填體滲透系數和比儲水系數之間的內在聯系進行闡述，以后會對其關系進行深入的探究和討論。

［1］ 周愛民.中國充填技術概述［C］∥第八屆國際充填采礦會議論文集.北京:中國有色金屬學會，2004.

［2］ 孫訥正.地下水流的數學模型和數值方法［M］.北京:地質出版社，1979.

［3］ 薛禹群，謝春紅.地下水數值模擬［M］.北京:科學出版社，2007.

［4］ 王君連.工程地下水計算［M］.北京:中國水利水電出版社，2004.

［5］ 孔祥言.高等滲流力學［M］.合肥:中國科學技術大學出版社，1999.