地鐵車站縱梁內力研究

楊 海

(中鐵隧道勘測設計院有限公司，天津 300133)

0 引言

近年來，隨著地鐵建設的快速發展，全國大多數省會城市及沿海地區經濟較發達的城市均已投入到地鐵建設當中，并且越來越多的城市有修建地鐵的計劃。據粗略統計，全國在建地鐵的城市已超過30個。鑒于設計單位前期設計經驗的積累和當前設計行業競爭愈趨激烈，如何在不影響工程質量的前提下降低工程成本成為當前提高設計水平的一項緊迫任務。在這種情況下，對結構設計的進一步優化和精細化提出了更高的要求。

針對地鐵車站板和側墻的優化設計，已有學者進行深入探究，如楊建學［1］、代坤［2］等均通過二維簡化與三維實體計算對比分析，找出二維計算中存在的一些不足和尚需改進的地方。由于二維計算中存在一些不合理的簡化，且無法按板梁協同受力分析，導致頂板及側墻內力在二維計算與三維計算時有較大差異。因為實際工程中縱梁與板協同受力，所以引起地鐵車站內力計算差異的主要因素為縱梁。當前對縱梁這一主要受力構件的研究還較少，尤其是采用傳統分析方法與三維分析方法的對比分析更鮮有研究，故本文將針對車站縱梁的受力進行探索、研究。因中縱梁和底縱梁與頂縱梁受力力學模型類似，故本文僅對頂縱梁的受力進行研究，以期為類似工程的設計提供一些參考。

1 計算模型

以單柱雙跨、雙柱三跨這2種典型形式的地鐵車站頂縱梁為分析研究對象，其結構平面布置見圖1和圖2。

圖1以某2層地下單柱雙跨車站的標準段作為分析實例，頂板覆土3 m，頂板厚800 mm(h0)，側墻厚700 mm，側墻間凈間距18.3 m，頂縱梁截面尺寸為1 200 mm×1 800 mm(b×h)，柱截面尺寸為1 000 mm×800 mm，柱中心距8.0 m。除柱采用C50混凝土外，其余結構構件均采用C35混凝土。

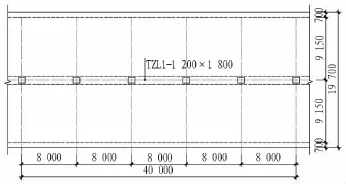
圖1 單柱雙跨車站頂縱梁結構平面布置圖(單位:mm)Fig.1 Plan layout of structure of longitudinal beam of singlecolumn two-span Metro station(mm)

圖2以某地下2層雙柱三跨車站的標準段作為分析實例，頂板覆土3 m，頂板厚800 mm(h0)，側墻厚700 mm，側墻間凈間距21.3 m，頂縱梁截面尺寸為1 000 mm×1 800 mm(b×h)，柱截面尺寸為1 000 mm×7 00 mm，柱中心距8.5 m，兩頂縱梁中心線間距6.0 m。除柱采用C50混凝土外，其余結構構件均采用C35混凝土。

圖2 雙柱三跨車站頂縱梁結構平面布置圖(單位:mm)Fig.2 Plan layout of structure of longitudinal beam of two-column triple-span Metro station(mm)

2 傳統方法分析

2.1 單柱雙跨站

在分析頂縱梁受力的時候，傳統方法是將頂板上部水土荷載及自重、超載等按板面荷載按照板凈寬的一半分擔到頂縱梁上，取1延米為荷載統計長度，計算荷載統計結果見表1。

表1 計算荷載統計表Table 1 Loads calculated kN/m

2.1.1 荷載設計值

根據文獻［3－6］的規定，按結構在施工階段和使用階段可能出現的最不利情況進行荷載組合。各種荷載組合及分項系數見表2。

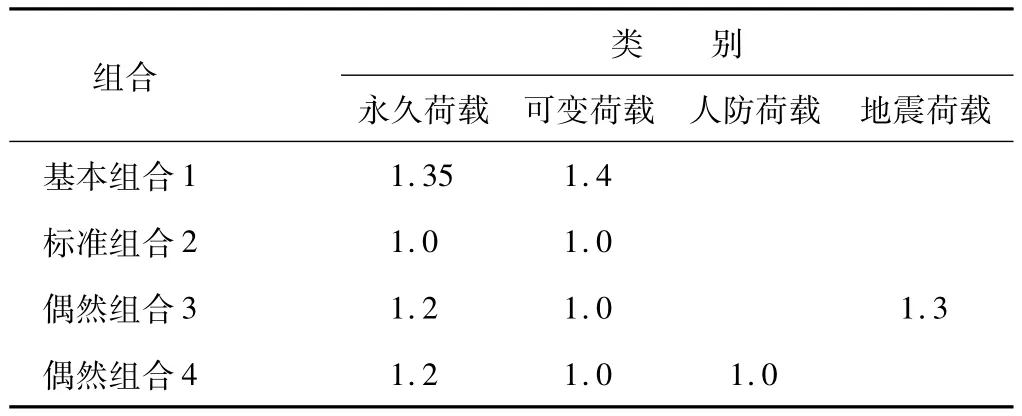
表2 荷載組合表Table 2 Load combination mode

基本組合考慮結構重要性系數1.1，人防荷載按6級人防抗力等級考慮，根據經驗和理論計算，偶然組合3，4不控制結構設計。以下分別計算基本組合1(承載能力極限狀態)和標準組合2(正常使用極限狀態)時的結構內力。

1)承載能力極限狀態時的荷載設計值

2)正常使用極限狀態時的荷載設計值

2.1.2 內力計算

1)頂縱梁取5跨，經計算承載力極限狀態下的內力圖(選取中間3跨)見圖3和圖4。

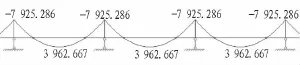
圖3 頂縱梁彎矩圖(單位:kN·m)Fig.3 Bending moment of longitudinal beam(kN·m)

圖4 頂縱梁剪力圖(單位:kN)Fig.4 Shear force of longitudinal beam(kN)

2)頂縱梁取5跨，經計算正常使用狀態下的內力圖(選取中間3跨)見圖5和圖6。

2.2 雙柱三跨站

計算方法和原則同單柱雙跨站，計算荷載統計結果見表3。

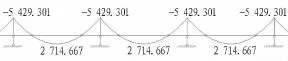
圖5 頂縱梁彎矩圖(單位:kN·m)Fig.5 Bending moment of longitudinal beam(kN·m)

圖6 頂縱梁剪力圖(單位:kN)Fig.6 Shear force of longitudinal beam(kN)

表3 計算荷載統計表Table 3 Loads calculated kN/m

2.2.1 荷載設計值

1)承載能力極限狀態時的荷載設計值

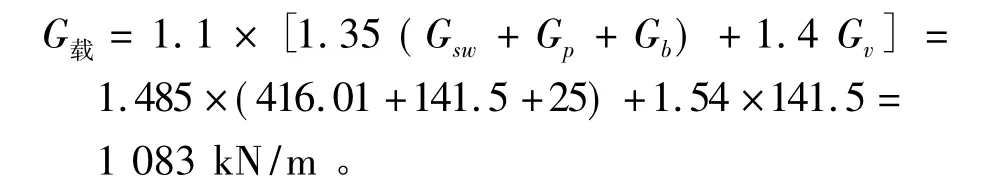
2)正常使用極限狀態時的荷載設計值

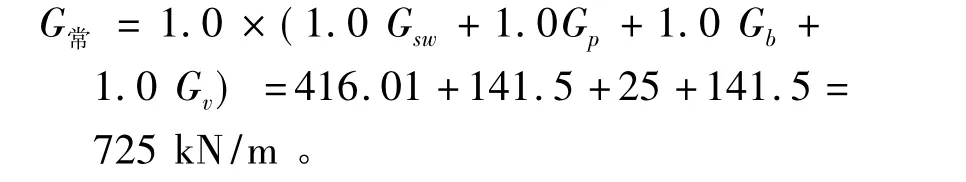
2.2.2 內力計算

1)頂縱梁取5跨，經計算承載力極限狀態下的內力圖(選取中間3跨)見圖7和圖8。

圖7 頂縱梁彎矩圖(單位:kN·m)Fig.7 Bending moment of longitudinal beam(kN·m)

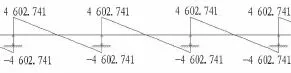
圖8 頂縱梁剪力圖(單位:kN)Fig.8 Shear force of longitudinal beam(kN)

2)頂縱梁取5跨，經計算正常使用狀態下的內力圖(選取中間3跨)見圖9和圖10。

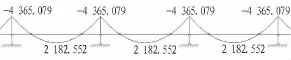
圖9 頂縱梁彎矩圖(單位:kN·m)Fig.9 Bending moment of longitudinal beam(kN·m)

圖10 頂縱梁剪力圖(單位:kN)Fig.10 Shear force of longitudinal beam(kN)

3 三維有限元分析

3.1 單柱雙跨站

相比傳統二維拆解、等效、忽略頂板本身剛度影響等分析方法，三維有限元分析方法更直接，也更接近實際情況。現以SAP2000通用有限元分析程序建立三維整體受力模型，頂板與側墻采用薄板單元，縱梁及柱采用桿件單元，頂板與側墻和縱梁之間剛性連接，頂板縱向兩端為自由，頂板以0.5 m×0.5 m來劃分網格，分析頂縱梁在構件協同受力狀態下的內力大小。由于本例只分析頂縱梁受力，所以僅取下部為固定支座的車站負一層三維結構來作為受力分析模型，見圖11。

圖11 三維結構計算實體圖Fig.11 3D structure calculation model

1)極限承載力狀態下頂縱梁的內力圖(選取中間3跨)見圖12和圖13。

圖12 頂縱梁彎矩圖(單位:kN·m)Fig.12 Bending moment of longitudinal beam(kN·m)

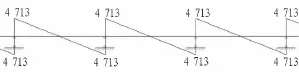
圖13 頂縱梁剪力圖(單位:kN)Fig.13 Shear force of longitudinal beam(kN)

2)正常使用狀態下頂縱梁的內力圖(選取中間3跨)見圖14和圖15。

圖14 頂縱梁彎矩圖(單位:kN·m)Fig.14 Bending moment of longitudinal beam(kN·m)

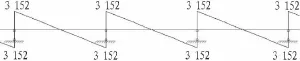
圖15 頂縱梁剪力圖(單位:kN)Fig.15 Shear force of longitudinal beam(kN)

3.2 雙柱三跨站

雙柱三跨站三維結構計算實體圖見圖16。

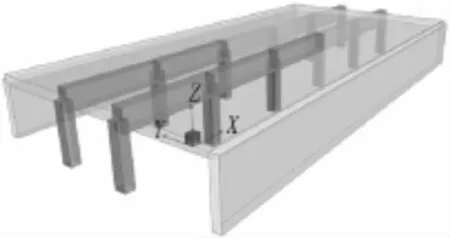
圖16 三維結構計算實體圖Fig.16 3D structure calculation model

1)極限承載力狀態下頂縱梁的內力圖(選取中間3跨)見圖17和圖18。

圖17 頂縱梁彎矩圖(單位:kN·m)Fig.17 Bending moment of longitudinal beam(kN·m)

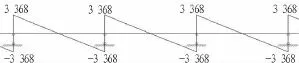
圖18 頂縱梁剪力圖(單位:kN)Fig.18 Shear force of longitudinal beam(kN)

2)正常使用狀態下頂縱梁的內力圖(選取中間3跨)見圖19和圖20。

圖19 頂縱梁彎矩圖(單位:kN·m)Fig.19 Bending moment of longitudinal beam(kN·m)

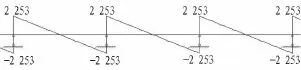
圖20 頂縱梁剪力圖(單位:kN)Fig.20 Shear force of longitudinal beam(kN)

4 對比分析

4.1 單柱雙跨站

根據統計結果，對比傳統方法 (簡稱二維)與三維有限元整體分析方法 (簡稱三維)的內力計算結果差異。

4.1.1 端部內力差異

1)彎矩差異(見表4)。

表4 彎矩對比表Table 4 Comparison of bending moment kN·m

2)剪力差異(見表5)。

表5 剪力對比表Table 5 Comparison of shear force kN

4.1.2 跨中內力差異

1)彎矩差異(見表6)。

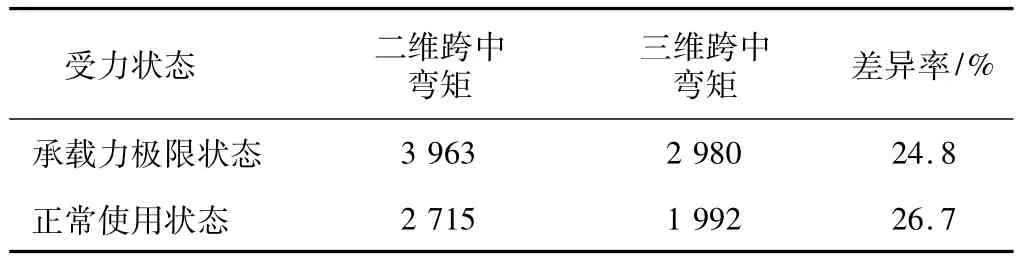
表6 彎矩對比表Table 6 Comparison of bending moment kN·m

2)跨中剪力均為零。

4.1.3 差異規律

1)二維計算內力結果均大于三維計算結果。

2)對于端部彎矩，二維比三維計算結果多15% ～20%。3)對于跨中彎矩，二維比三維計算結果多25%左右。4)剪力大小差異在20%左右，按6肢箍來計算配置箍筋，相差約1個箍筋直徑大小等級。

5)結構所受荷載大小增減與彎矩、剪力差異百分比均成反向變化關系。即結構所受荷載越大，彎矩、剪力差異越小;反之則差異越大。

4.2 雙柱三跨站

根據統計結果，對比傳統方法(簡稱二維)與三維有限元整體分析方法(簡稱三維)的內力計算結果差異。

4.2.1 端部內力差異

1)彎矩差異(見表7)。

表7 彎矩對比表Table 7 Comparison of bending moment kN·m

2)剪力差異(見表8)。

表8 剪力對比表Table 8 Comparison of shear force kN

4.2.2 跨中內力差異

1)彎矩差異(見表9)。

表9 彎矩對比表Table 9 Comparison of bending moment kN·m

2)跨中剪力均為零。

4.2.3 差異規律

1)二維計算內力結果均大于三維計算結果。

2)對于端部彎矩，二維比三維計算結果多25%左右。

3)對于跨中彎矩，二維比三維計算結果多30%左右。

4)剪力大小差異在27%左右，按6肢箍來計算配置箍筋，相差約1個箍筋直徑大小等級。

5)結構所受荷載大小增減對彎矩、剪力差異百分比變化率影響不明顯。

5 結論與建議

因地鐵車站各縱梁結構受力力學模型相似，故通過對頂縱梁的分析，可知底縱梁、中縱梁與頂縱梁有同樣或類似的結論。

1)不論單柱雙跨還是雙柱三跨典型車站的縱梁內力大小，傳統分析方法與三維有限元分析方法之間的差異具有相似的規律。

2)傳統方法分析的內力均大于三維有限元分析的內力。

3)根據前面荷載變化與計算差異率的規律可知，單柱雙跨車站縱梁的計算差異對覆土厚度較敏感;雙柱三跨車站縱梁的計算差異對覆土厚度不敏感。

4)對于端部彎矩，二維計算比三維計算大15% ～25%。

5)對于跨中彎矩，二維計算比三維計算大25% ～35%。

6)對于支座剪力，二維計算比三維計算大20% ～30%。

產生這種差異的根本原因在于二維計算中無法分析板梁協同受力的空間作用，而三維計算則能分析板梁協同受力的空間作用，所以三維計算結果與結構實際受力更接近。

與三維有限元計算方法相比，傳統計算方法較快捷，并且計算結果也能基本滿足工程設計需要，但是其合理性和精細化程度有待提高。為了提高結構設計質量，在沿用傳統方法計算時，結合工程實際經驗，建議對寬度在19.7 ～22.7 m、柱跨在 8.0 ～8.5 m 的淺埋地鐵車站的二維計算結果進行適當調整。

折減后的二維計算結果更接近結構實際受力狀況，減少了工程中不必要的浪費。在以后的設計中，最好采用三維計算。建議下一步可對不同板跨、不同柱距和不同覆土條件下的縱梁受力進行全面、深入的研究。

［1］ 楊建學.明挖地鐵車站不同計算方法計算結果比較［J］.甘肅科技，2009(13):133－136.

［2］ 代坤.明挖地鐵車站空間計算模型與平面計算模型的對比分析［J］.隧道建設，2010，30(S1):254－258.(DAI Kun.Comparative analysis on 3D cmputation model and 1D cmputation model for Metro sations constructed by cut and cover method ［J］.Tunnel Construction，2010，30(S1):254－258.(in Chinese))

［3］ 中國建筑科學研究院.GB 0009—2012建筑結構荷載規范［S］.北京:中國建筑工業出版社，2012:9－12.

［4］ 中國建筑科學研究院.GB 50011—2010建筑抗震設計規范［S］.北京:中國建筑工業出版社，2010:31－43.

［5］ 中國建筑設計研究院.GB 50038—2005人民防空地下室設計規范［S］.北京:中國建筑工業出版社，2005:88－107.

［6］ 北京城建設計研究總院.GB 50157—2003地鐵設計規范［S］.北京:中國計劃出版社，2003.

［7］ 中國建筑科學研究院.GB 50010—2010混凝土結構設計規范［S］.北京:中國建筑工業出版社，2010.