LuI3閃爍晶體的第一性原理研究*

鄧嬌嬌 劉波 顧牡

(同濟大學物理系,上海市特殊人工微結構材料與技術重點實驗室,上海 200092)

1 引言

閃爍體是一種輻射探測用功能材料,通過吸收高能粒子或射線,并把吸收的能量轉化為可見光,從而實現對粒子和射線的探測.由于具備高光產額、快衰減等特性,摻雜Ce3+離子的镥基閃爍體備受關注[1,2],有些晶體已經較為成熟,例如Lu2SiO5:Ce[3,4].近年來一種新的镥基閃爍體LuI3:Ce3+也逐漸進入人們的視野,該材料密度為5.6 g/cm3,具有很高的光產額(最高的報道可達76000 ph/MeV),是Lu2SiO5:Ce的兩倍,在γ射線激發下產生峰值位于474 nm的發射,具有23—31 ns的快衰減,662 keVγ射線激發下的能量分辨率為11%[5,6].其發光來源于Ce3+的5d到4f的宇稱允許躍遷,光產額決定于該摻雜離子的躍遷概率和基質的性質.目前制備LuI3:Ce3+單晶的方法主要是坩堝下降法(Bridgman)[5?7],這是一個有望長出大尺寸單晶的生長方法.由于LuI3:Ce3+具有強烈的潮解特性,生長出的晶體必須采用合適的封裝方法才可以測試和應用.盡管目前高質量、大尺寸的晶體生長還存在一定難度,但其高的光產額和快的衰減時間使得該材料有望在閃爍探測領域發揮重要作用,例如高能物理與核物理實驗、醫學成像、無損檢測、核輻射檢測和地球物理勘探等.

對于該新型閃爍體基質材料的研究還剛剛起步,對其基本物理性質的認識還遠遠不夠,這制約了對其閃爍特性的優化和提高.第一性原理基于材料的構成元素和結構,通過理論計算得出材料的各項物理性質,在閃爍材料中有重要應用[8?10].本文采用第一性原理研究LuI3的結構、電子性質和理論光產額,期待這些結果對于認識其發光機理,提高閃爍特性有一定的幫助.

2 計算方法

LuI3晶體屬于BiI3型結構,空間群R-3(編號:148).晶格參數實驗值為a=(7.39±0.01)?,c=(20.71±0.02)?[11].密度5.68 g/cm3,有效原子數Zeff=60.21.

計算采用基于贗勢和平面波方法的ABINIT程序包[12].將離子勢用贗勢替代,電子波函數通過平面波基組展開.贗勢文件是重要的輸入文件,我們采用廣義梯度近似(GGA)[13]和局域密度近似(LDA)[14]來描述電子與電子相互作用的交換關聯勢.選取的贗勢如表1所示.

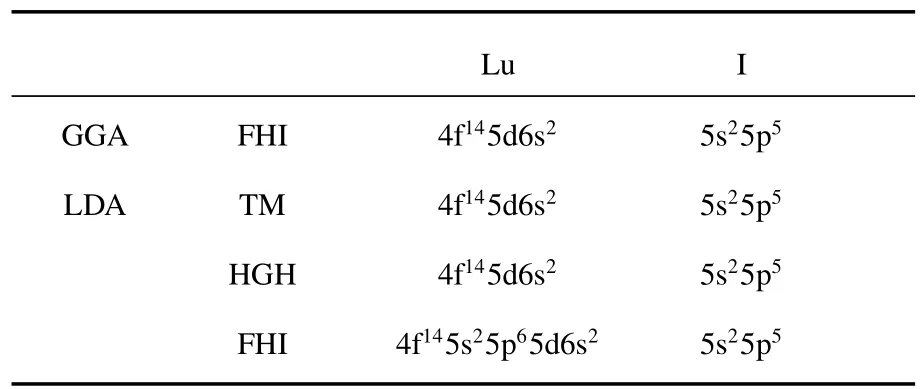
表1 贗勢的種類以及價電子

計算首先進行了贗勢截止能量和布里淵區k點網格 (按照 Monkhorst-Pack方法分割)的收斂測試.在自洽計算過程中,使用共軛梯度算法,當兩次計算所得到的LuI3原胞總能量差值小于1 meV/atom時,認為計算達到收斂要求.收斂測試表明LDA-TM,LDA-HGH,LDA-FHI,GGA-FHI四種贗勢的截止能量分別為40,60,50和50 Ha,網格k點6×6×6時滿足收斂要求.

3 結果與討論

3.1 幾何優化

幾何優化采用的是BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法[15].幾何優化后的晶胞處于能量最低狀態,收斂標準定為每個原子上的剩余力小于0.01 eV/?.表2為LuI3優化后的結果.

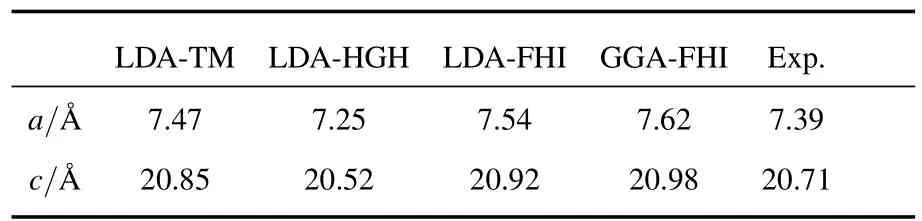
表2 不同贗勢下晶格常數計算值與實驗值比較

結果表明LDA-TM贗勢能得到較好的結果,幾何優化得到的理論晶格常數與實驗值的差別在1%以內.在四種贗勢中,LDA-TM贗勢的截止能量也較小,且幾何優化的結果與實驗值最為吻合,所以后面的計算都采用LDA-TM贗勢.

3.2 體模量

通過計算,得到晶體原胞體積與能量的關系,如圖1所示.

對圖1中計算的能量與體積關系,采用(1)式所示的三階Birch-Mrunaghan狀態方程進行擬合,得到LuI3的體模量為89.5 GPa,體模量對壓強的一階導數為4.6.

其中,B0為體模量,為體模量對壓強的一階導數,V0為平衡體積,E0為平衡條件下的能量.

雖然沒能在文獻中查到體模量的實驗值,只能作為一種理論預測,但一般而言,熔點高的晶體體模量也高.CuI晶體的體模量是31 GPa[16],LuI3晶體(熔點為1050?C)體模量的計算值比CuI晶體(熔點為606?C)的大,一方面是由于LuI3晶體的熔點高,另一方面是因為镥原子的原子序數大,使得晶體比較硬.這也從側面證明了計算的合理性.

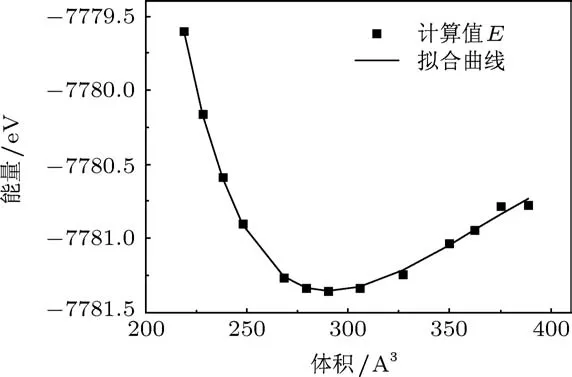
圖1 LuI3能量和體積的計算曲線

3.3 電子結構

采用幾何優化的晶格參數,計算了LuI3晶體在第一Brillouin區中高對稱點及某些高對稱方向上的能量值.圖2中的LuI3能帶結構顯示出了其具有典型離子晶體特征的平坦帶結構.我們將價帶頂設為0 eV,從圖中可以看出在導帶以上2—3 eV的能量范圍內有類拋物線狀的能帶,這是來自Lu的s電子的貢獻;在價帶頂附近有若干條能量非常局域的能帶,對應了d電子帶.價帶頂位于Γ點,導帶底位于L點,能帶具有間接帶隙結構.帶隙的計算值為2.488 eV,實驗值為4.3 eV[17],這樣大的誤差主要來源于計算中采用的交換關聯勢部分考慮了電子的交換作用,對于大多數含有s或p電子的體系而言是一個較好的近似,但對于含有d,f電子的體系,電子間的關聯作用很強,計算誤差大.

圖2 LuI3的能帶結構

圖3 LuI3總態密度和分態密度

圖3是LuI3的總態密度和分態密度圖.將價帶頂設為0 eV,結合LuI3的總態密度圖和各原子的分態密度圖可以得出:?4.4 eV附近有一個寬度約為0.2 eV的窄帶,主要是Lu的4f態;?3.55—0 eV之間的態組成了價帶(VB),這主要是I的5p態;2.44—12.35 eV之間的態組成了LuI3的導帶,這主要來源于Lu的5d態,其中還含有少量的Lu的6s態的貢獻.在?3.46 eV處,Lu的6s態、4f態和I的5p態同時出現了尖峰,說明相鄰的Lu原子的6s態,4f態與I原子的5p態之間的相互作用強,出現了雜化峰.

3.4 光產額

晶體的光產額可以通過公式LY=(106/βEg)SQ確定[18],其中,LY為光產額,Eg為材料的能隙,β為轉換效率(對于大多數半導體和絕緣體材料,轉換效率β的值為2—3),S為能量傳遞效率,Q為發光中心的量子效率.從公式中可以看出材料的能隙對光產額的影響很大,能隙越小光產額越大.但事實上作為有效的Ce3+發光的基質還必須使得Ce3+的5d態位于帶隙中,這就導致帶隙也不能太小.根據公式我們估算出LuI3晶體的理論光產額約為100000 ph/MeV(β取2.5,理想條件下S與Q均取為1),這是一個相當高的數值,主要得益于LuI3的帶隙適中,然而實驗中測得晶體的光產額最高值為76000 ph/MeV,低于理論光產額,質量不高的晶體光產額可能更低.因此采用結構調控的方法提高能量傳遞效率,降低無輻射躍遷和缺陷中心的方法可能提高材料的光產額.

4 結論

本文基于第一性原理的贗勢平面波方法,分別采用LDA-TM,LDA-HGH,LDA-FHI,GGA-FHI四種贗勢對LuI3晶胞進行了結構優化.其中,LDATM贗勢能得到較好的結果,晶格常數的理論值與實驗值符合得較好.在LDA-TM贗勢下計算了LuI3晶體的能帶結構和態密度,結果顯示LuI3晶體屬間接帶隙材料,價帶主要來源于I的5p態,導帶主要來源于Lu的5d態,很少部分來自Lu的6s態.該材料有很高的理論光產額,高質量晶體的獲得對于其成為實用的閃爍晶體至關重要.

[1]Canning A,Chaudhry A,Boutchko R,Gr?nbech-Jensen N 2011 Phys.Rev.B 83 125115

[2]Wang D W,Huang S H,You F T,Tao Y 2009 Chin.Phys.C 33 1019

[3]Liu B,Shi C S,Yin M,Fu Y B,Zhang G B,Ren G H 2006 J.Lumin.117 129

[4]Liu B,Shi C S 2002 Sci.Bull.47 1(in Chinese)[劉波,施朝淑2002科學通報47 1]

[5]Birowosuto M D,Dorenbos P,Haas T J,Eijk C W E,Kramer K W,Gudel H U 2006 J.Lumin.118 308

[6]Glodo J,Shah K S,Klugerman M,Wong P,Higgins B,Dorenbos P 2005 Nucl.Instrum.Methods Phys.Res.A 537 279

[7]Shah K S,Glodo J,Klugerman M,Higgins W,Gupta T,Wong P,Moses W W,Derenzo S E,Weber M J,Dorenbos P 2004 IEEE Trans.Nucl.Sci.51 2302

[8]Liu B,Gu M,Qi Z M,Liu X L,Huang S M,Ni C 2007 Phys.Rev.B 76 064307

[9]Deng J J,Liu B,Gu M,Liu X L,Huang S M,Ni C 2012 Acta Phys.Sin.61 036105(in Chinese)[鄧嬌嬌,劉波,顧牡,劉小林,黃世明,倪晨2012物理學報61 036105]

[10]Tong H Y,Gu M,Tang X F,Liang L,Yao M Z 2000 Acta Phys.Sin.49 1545[童宏勇,顧牡,湯學峰,梁玲,姚明珍2000物理學報49 1545]

[11]Asprey L B,Keenan T K,Kruse F H 1964 Inorgan.Chem.3 1137

[12]Gonze X,Beuken J M,Caracas R,Detraux F,Fuchs M,Rignanese G M,Sindic L,Verstraete M,Zerah G,Jollet F,Torrent M,Roy A,Mikami M,Ghosez P,Raty J Y,Allan D C 2002 Comput.Mater.Sci.25 478

[13]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[14]Kohn W,Sham L J 1965 Phys.Rev.140 1133

[15]Press W H,Flannery B P,Teukolsky S A,Vetterling W T 1986 Numerical Recipes,the Art of Scientific Computing(Cambridge University Press)p308

[16]Hoffman M,Hull S,Keen D A 1995 Phys.Rev.B 51 12022

[17]Vasil’ev A N,Iskandarova I M,Scherbinin A V,Markov I A,Bagatur’yants A A,Potapkin B V,Srivastava A M,Vartuli J S,Duclos S J 2009 J.Lumin.129 1555

[18]Weber M J 2004 Nucl.Instrum.Methods Phys.Res.A 527 9