基于SIMP 理論的電動汽車車身多目標拓撲優化

謝倫杰，張維剛，常偉波，崔 杰

(湖南大學，汽車車身先進設計制造國家重點實驗室，長沙 410082)

前言

拓撲優化是一種根據約束、載荷和優化目標而尋求材料最佳分配的優化方法，主要應用在產品開發的概念設計階段。拓撲優化在設計初始階段即被引入，可優化空間大，對最終產品的成本和性能有非常重要的影響［1］。電動汽車能有效解決能源短缺和環境污染問題，已成為汽車行業的研究熱點。由于驅動、儲能裝置的特殊性，傳統的車身結構難以滿足電動汽車的性能要求［2］;電動汽車主要通過柔性的電線傳遞能量，其各部件的布置具有很大的靈活性，這為拓撲優化創造了有利的條件。

目前電動汽車車身的拓撲優化主要集中在單目標的優化分析［3-5］，但車身結構作為承載基體，須滿足多種靜態工況和動態工況下的性能要求，是一個多目標拓撲優化問題［6］。為了同時滿足電動汽車車身多種靜態載荷工況和動態頻率特性的要求，本文中以平均柔度最小和平均頻率最大為總目標，對電動汽車車身實現多目標拓撲優化，得到較為清晰的承載結構，避免了單目標拓撲優化無法同時考慮其他因素的缺點。

1 拓撲優化數學模型及算法

1.1 SIMP插值模型

拓撲優化是一個“0-1”問題，即結構件材料的“有”與“無”的問題。由于不可能把設計區域中的每個點都作為一個設計變量，故必須對設計區域進行離散，但離散問題在數學上很難處理，通常將此問題轉化為連續問題去研究，變密度法就是這一思路的產物［7］，其基本思想是人為引入一種假想的密度可變材料，優化時以材料密度為設計變量，將結構拓撲優化問題轉換為材料的最優分布問題。

文獻［8］中對密度法材料插值模型進行研究，提出一種基于正交各向同性材料密度冪指數形式的帶懲罰的實體各向同性材料(solid isotropic material with punishment，SIPM)，即變密度法材料密度插值理論。優化時以單元設計變量的大小決定單元取舍，采用懲罰因子約束抑制介于0～1之間的單元，使中間密度值盡量向0與1兩端聚集，使連續變量的拓撲優化模型能很好地逼近0-1離散變量的優化模型。SIMP材料插值模型假設材料的彈性張量各向同性，泊松比為與密度無關的常量，材料屬性隨著單元相對密度的變化而變化，其具體關系式［9］為

式中:E0和E(ρ)為初始和優化后彈性模量;K0和K(ρ)為初始和優化后剛度矩陣;P為懲罰因子，P＞1;ρ為材料密度;ρmin為材料為空的最小密度值。

1.2 拓撲優化數學模型

1.2.1 靜態拓撲優化數學模型

靜態單工況下，以結構單元的相對密度作為設計變量，以體積分數作為約束條件，以結構柔度的最小化(即剛度最大化)作為目標函數，建立基于SIMP理論的連續體結構拓撲優化數學模型:

式中:ρi為結構單元的相對密度;C為結構的總體柔度;U為位移矩陣;P為懲罰因子;K為優化前的結構總剛度矩陣;F為力列向量;ui為單元位移列向量;k0為結構初始單元剛度矩陣;V為優化后的結構總體積;V0為初始結構總體積;α為體積分數;vi為優化后的單元體積;ρmin為設計變量的下限，其目的是防止單元剛度矩陣奇異。

多工況情況下，不同的載荷工況將得到不同的拓撲結構。傳統的多工況優化問題采用線性加權疊加法將多目標問題轉化為單目標問題求解，但對于非凸優化問題來說，該方法不能確保得到的所有帕累托(pareto)解為最優解［10］，故采用折衷規劃法結合功效函數法來解決此問題。折衷規劃法的基本思想是把多個子目標函數正規化，并給每個子目標加權后合成一個單目標。功效函數法是根據多目標規劃原理，對每一項子目標確定一個理想值和不允許值，以理想值為上限，不允許值為下限，再經過加權平均進行綜合，從而評價被研究對象的綜合狀況［11］。由折衷規劃法結合功效函數法得到靜態多工況下拓撲優化的目標函數:

式中:m為載荷工況總數;wk為第k個工況的權值;P為懲罰因子(P≥2);Ck(ρ)為第k個工況的柔度目標函數、分別為第k個工況柔度目標函數的最大值和最小值。

1.2.2 動態拓撲優化數學模型

動態拓撲優化是為了改善結構的模態特性。如果將某一階頻率的最大化作為目標函數，在優化迭代過程中，由于結構材料的刪除等修改，當一個階次的頻率達到最大時，其他階次的頻率可能降到一個較低的值，幾階頻率之間可能相互調換次序，發生模態交換現象，從而引起振蕩并干擾模型求解收斂，使優化設計的收斂性和穩定性得不到保證。為了克服這種現象，采用平均頻率公式［12］來定義優化的目標函數，建立動態頻率拓撲優化數學模型:

式中:Λ(ρ)為平均頻率;λj為第 j階特征頻率;λ0、s為給定的參數，用來調整目標函數;wj為第j階頻率的權值系數;f為需要優化的低階頻率的階次;M為總質量矩陣;φj是第j階振型向量。

1.2.3 靜態-動態聯合拓撲優化數學模型

為了使優化結果具有良好的靜態特性和動態特性，同時考慮靜態剛度目標和動態振動頻率目標為拓撲優化的總目標函數。由于兩者的數量級存在較大的差異，計算時容易忽略小數量級目標函數在優化中的作用，使計算結果受到數量級高的目標函數的支配。為了平衡兩者數量級之間的差異，目標函數先經如下形式的歸一化定義:

式中:fi(x)為第i個目標函數;wi為第i個目標函數的權系數;x為設計變量;si為標度因子，使每個目標函數有相同數量級，并在優化中占有同等地位。

建立靜態-動態聯合拓撲優化數學模型如下:

式中:F(ρ)為靜動態聯合總目標函數;w為柔度目標函數的權重;Λmin、Λmax分別為頻率目標函數的最小值和最大值，用來消除量綱。

1.3 拓撲優化求解算法

連續體結構拓撲優化的求解算法主要有優化準則法和數學規劃法。其中數學歸納法求解結構優化問題時，通常需要計算目標函數、約束函數和它們的導數，計算效率較低。優化準則法是一種間接優化方法，不直接優化目標函數，而是把數學中最優解應滿足的庫恩塔克(Kuhn-Tucker)條件作為最優結構應滿足的準則來更新設計變量和拉格朗日乘子，收斂速度快，迭代次數少且與結構大小和復雜程度無關，尤其對體積約束下的最小柔度問題的求解更為有效［13］，因此采用優化準則法求解并構造拉格朗日(Lagrange)函數:

式中:η1、η2、η3、η4為拉格朗日乘子，η1為標量，η2、η3、η4為向量;ρ 是 ρi組成的向量;ai、bi為松馳因子。由此可得庫恩塔克條件和設計變量迭代公式:

1.4 拓撲優化流程

利用Hypermesh軟件的Optistruct模塊進行拓撲優化的流程如圖1所示。

2 電動汽車車身拓撲優化

2.1 載荷工況分析

依據電動汽車的使用情況和實際載荷工況，選擇以下4種典型工況作為模型分析載荷工況。

(1)彎曲工況 彎曲工況模擬電動汽車四輪著地、勻速直線行駛。考慮滿載情況，車上共有4名乘員，每位乘員體質量為65kg，行李總質量為40kg。約束左前輪全部自由度和其余3輪z方向上的平動自由度。

(2)扭轉工況 扭轉工況模擬各車輪懸空狀態，分別釋放對應懸空車輪的全部自由度，同時在懸空一端的車軸上施加一極限轉矩(車軸負荷的一半乘以輪距)，約束懸空同軸對稱車輪除x方向平動自由度以外的全部自由度和其他兩輪的全部自由度。

(3)緊急制動工況 緊急制動工況主要考慮電動汽車以最大減速度制動時，地面制動力對車身的影響。在x方向上附加-0.8g的慣性力。約束前輪的全部自由度和后輪除x方向平動自由度外的全部自由度。

(4)急轉彎工況 主要考慮當電動汽車以最大轉向速度轉彎時，慣性力對車身的影響。在y方向附加0.4g的離心力。釋放一側車輪y方向的平動自由度，約束另一側車輪的全部自由度。

2.2 拓撲優化計算

根據電動汽車的結構布置特點，扣除乘員艙、行李艙、動力總成、輪胎包絡和風窗玻璃等所占據的部分，確定剩余部分為優化設計空間如圖2所示。在Hypermesh軟件中采用六面體單元劃分網格，定義材料屬性，確定載荷和邊界條件，建立拓撲優化有限元模型。

多目標拓撲優化的函數公式在OptiStruct軟件中不能直接調用，因此借助于軟件中的用戶自定義方程功能來實現。先定義靜態折衷規劃公式和動態平均頻率公式，然后把定義好的函數設為響應，最后把該響應作為目標函數進行拓撲優化。

在進行單目標拓撲優化時發現，以剛度作為目標函數進行優化時，平均柔度達到最優，但平均特征值卻很小;而以頻率作為目標函數進行優化時，平均特征值達到最優，但平均柔度卻很大。這表明靜態剛度和動態頻率是兩個相互矛盾的目標函數，權重分配相差過大時難以使剛度和頻率目標函數同時達到最優，而車身結構作為各個部件的承載基體，首先應保證其剛度要求，出于這樣的考慮，取柔度目標函數的權值為0.6，頻率目標函數的權值為0.4。

以優化設計空間內每個單元的相對密度為設計變量，以體積分數為約束，以自定義的靜動態聯合總函數公式為目標函數，在OptiStruct軟件中建立拓撲優化計算模型。由于約束條件對最終的拓撲優化結果影響較大，因此先分別選取體積分數α為0.2和0.4的約束條件進行拓撲優化試計算，假定單元相對密度在0.15以下的區域為無材料分布，優化結果如圖3所示。

從試算結果可以看出，約束為α=0.2時，刪除材料單元過多，約束為α=0.4時，保留材料單元過多，均不是最佳的材料布局方式。選取約束為α=0.3進行拓撲優化計算，求解拉格朗日乘子，采用優化準則算法計算迭代因子，更新設計變量。經過30步迭代計算，沒有發生振蕩現象，目標函數趨于收斂，其收斂曲線如圖4所示，拓撲優化結果如圖5所示。通過對優化結果觀察可以發現清晰的載荷路徑，圖6為截取前艙部分的載荷路徑。

拓撲優化計算結果對車身結構的載荷傳遞路徑和材料布局方式具有指導意義，但與工程實際仍有較大的距離，根據實際情況和經驗資料進行適當的修正后初步確定電動汽車車身結構如圖7所示。

3 拓撲優化結果分析

由于所研究對象為微型電動汽車，根據廠家的設計用途，該電動汽車主要作為城市代步工具使用，最高行駛速度的設計要低于傳統燃油汽車，使用環境和極限工況也優于傳統燃油汽車，因而其車身的設計要求也相應地低于同類型的傳統燃油汽車。依據拓撲優化分析結果，建立相應的有限元模型，對其靜動態結構特性進行分析，驗證優化設計方案的可行性。有限元靜態分析結果如表1所示。從表1中可以發現，各載荷工況的應力最大值均在材料應力的許可值范圍內，其中最大應力為141.1MPa，最大變形為7.6mm，出現在扭轉工況的后懸支撐與車架連接區域;其余各工況下最大應力均小于100MPa，最大變形為2～3mm，車身結構基本滿足靜態剛度設計要求。在下一步的詳細設計中，扭轉工況下的車身結構剛度可以做進一步的優化改進。

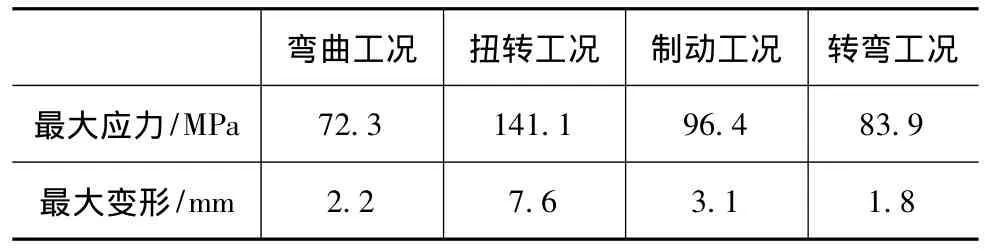
表1 有限元靜態分析結果

由于低頻振動比高頻振動危險，前幾階振動對結構的動態性能影響較大，故模態分析中只選取前5階的模態振型進行分析，結果如表2所示。由于電動汽車的驅動裝置采用平衡性更好的電機代替傳統的發動機，有效減少了整車的振動激勵;而路面激勵隨道路條件決定，高速公路和城市較好路面的激勵多在3Hz以下，因而只須重點校驗車身結構的低階頻率是否高于非簧載結構的固有頻率(一般為6～15Hz)。由表中數據可以看出，前3階的振動頻率為24.4～54.5Hz，有效地避開了路面對汽車的激勵頻率范圍，且高于非簧載質量的固有頻率，避免了共振的產生。從頻率分布上看，1階扭轉振型頻率為24.4Hz，1階彎曲振型頻率為36.2Hz，車身整體彎曲剛度大于扭轉剛度，兩種固有頻率明顯錯開，主要的彎扭模態沒有耦合。

表2 有限元動態分析結果

4 結論

對電動汽車車身結構靜動態多目標拓撲優化方法進行探討。基于SIMP材料插值理論，在對目標函數進行歸一化以消除數量級差異后，以平均柔度最小和平均頻率最大為總目標，利用優化準則法建立設計變量的迭代方程，同時考慮約束條件對優化結果的影響，選取不同的體積分數對電動汽車車身結構進行拓撲優化，得到車體結構清晰、載荷路徑明顯的優化結果。有限元分析結果表明，采用此方法設計的車身結構具有較好的靜動態特性，滿足設計要求。該方法為電動汽車車身各部件的下一步詳細設計和其它車型的車身開發提供思路和參考依據。

［1］Bendsoe M P，Sigmund O.Topology Optimization:Theory，Methods and Applications［M］.Berlin:Springer，2003.

［2］謝慶喜，張維剛，鐘志華.電動汽車電池架的耐撞性仿真設計與優化［J］.汽車科技，2005，5(3):25-28.

［3］高云凱，姜欣，張榮榮.電動改裝轎車車身結構優化設計分析［J］.汽車工程，2005，27(1):115-117.

［4］丁利.結構拓撲優化分析在電動小車車身的輕量化的應用［J］.中國制造業信息化，2009，38(11):58-60.

［5］徐曉瑜，郭永進.電動低速汽車車身結構剛度約束拓撲優化設計［J］.機械設計與研究，2010，26(2):110-113.

［6］Chen T Y，Wu S C.Multi-objective Optimal Topology Design of Structures［J］.Computational Mechanics，1999，17(4):269-278.

［7］范文杰，范子杰，桂良進，等.多工況下客車車架結構多剛度拓撲優化設計研究［J］.汽車工程，2008，30(6):531-533.

［8］Bendsoe M P，Sigmund O.Material Interpolation Schemes in Topology Optimization［J］.Arch Appl Mech，1999，69:635-654.

［9］左孔天，陳立平，鐘糗芳，等.基于人工材料密度的新型拓撲優化理論和算法研究［J］.機械工程學報，2004，40(12):31-37.

［10］Min S，Nishiwaki S，Kikuchi N.Unified Topology Design of Static and Vibrating Structures Using Multi-objective Optimization［J］.Computers and Structures，2000，75:93-116.

［11］Marler R T，Arora J S.Survey of Multi-objective Optimization Methods for Engineering［J］.Struct Multidisc Optim，2004，26:369-395.

［12］Ma Z D，Kikuchi N.Topological Design for Vibrating Structures［J］.Comput.Methods Appl.Mech.Engrg，1995，121:259-280.

［13］孫靖民.機械優化設計［M］.北京:機械工業出版社，2005:167-172.